On appelle rotation la transformation géométrique qui fait tourner une figure autour d'un point fixe appelé centre de rotation, selon un angle. Ainsi, une rotation |r| est définie par son centre |O| et son angle |\theta|. On note donc une rotation comme ceci : |r_{(O,\,\theta)}.|
Certaines rotations particulières peuvent être définies par les règles suivantes lorsqu'elles sont centrées à l’origine |O=(0,0)| :
|r_{(O,90°)}| ou |r_{(O,-270°)} : (x , y) \mapsto (-y , x)| pour une rotation de |90°| ou |-270°|.
|r_{(O,180°)}| ou |r_{(O,-180°)} : (x , y) \mapsto (-x , -y)| pour une rotation de |180°| ou |-180°|.
|r_{(O,270°)}| ou |r_{(O,-90°)} : (x , y) \mapsto (y , -x)| pour une rotation de |270°| ou |-90°|.
|x| et |y| sont les coordonnées du point qui subit la rotation.
Des rotations de |180°| ou de |-180°| sont équivalentes. Elles amènent la figure initiale à la moitié d’un tour complet autour de l’origine. C’est pour cette raison qu’elles partagent la même règle de rotation.
Le sens positif d’une rotation suit le sens contraire des aiguilles d’une horloge (sens antihoraire).
Une rotation de |90°| signifie donc une rotation de |90°| dans le sens contraire des aiguilles d’une horloge (on passe de midi à 9 h, par exemple).
Au contraire, une rotation de |-90°| signifie une rotation de |90°| dans le sens des aiguilles d'une horloge (on passe de midi à 3 h, par exemple).
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><strong>Pourquoi, quand on tourne dans le sens positif, suit-on le sens antihoraire?</strong><br>
<br>
Les sens positif et négatif sont en lien avec la numérotation des <a href="/fr/eleves/bv/mathematiques/le-plan-cartesien-m1309">quadrants</a>. Les quadrants sont numérotés dans le sens antihoraire. Quand on tourne dans le même sens que la numérotation des quadrants, on suit le sens positif. </p>
</body></html>
Effectue une rotation centrée à l’origine de |90°| dans le sens horaire.
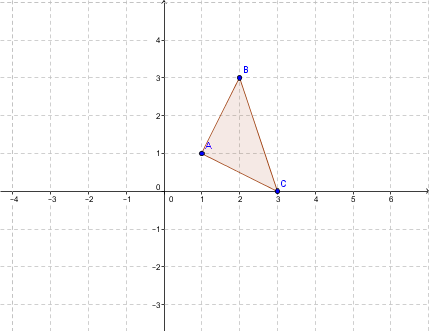
Étape 1 : Bien identifier les informations de la rotation.
Centre : |(0, 0)|
Grandeur : |90°|
Sens : horaire
C’est une rotation de |-90°| (sens horaire donc signe négatif). La règle associée à cette rotation est la suivante : |r_{(O, -90°)}:(x,y)\mapsto (y,-x)|.
Étape 2 : On identifie les sommets de la figure initiale.
|A (1, 1)|
|B (2, 3)|
|C (3, 0)|
Étape 3 : À l’aide de la règle de rotation, on trouve les coordonnées des sommets de la figure image.
La règle énonce que la coordonnée qui était en |y| (figure initiale) prend la place du |x| (dans la figure finale). Ensuite, la coordonnée qui était en |x| (figure initiale) doit changer de signe et prendre la place du |y| (dans la figure finale).
|A (1, 1) \mapsto (1, -1) = A’|
|B (2, 3) \mapsto (3, -2) = B’|
|C (3, 0) \mapsto (0, -3) = C’|
Étape 4 : Les nouvelles coordonnées sont celles de l'image de la figure initiale ayant subi une rotation de |-90°|.
On trace le triangle image.
L'image suivante illustre le déplacement de |90°| dans le sens horaire de chaque point par rapport au centre :
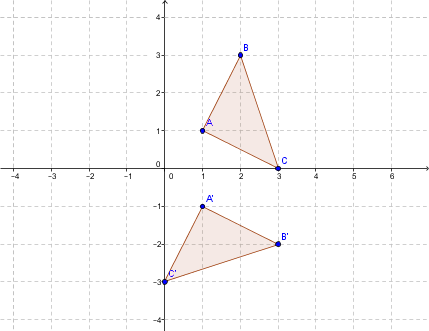
Si le centre de rotation n'est pas à l'origine:
On doit d'abord effectuer une translation pour ramener le centre de rotation à l'origine du plan cartésien. La translation est appliquée à tous les sommets de la figure initiale.
Ensuite, on effectue la rotation selon la règle.
Enfin, on effectue la translation inverse. Ainsi, si on a effectué la translation |t_{(a,b)}|, on doit effectuer la translation |t_{(-a,-b)}|.
Effectue la rotation du triangle |ABC|. Cette rotation doit être centrée au point |(-1,2)| et elle doit avoir un angle de |90°| dans le sens antihoraire.
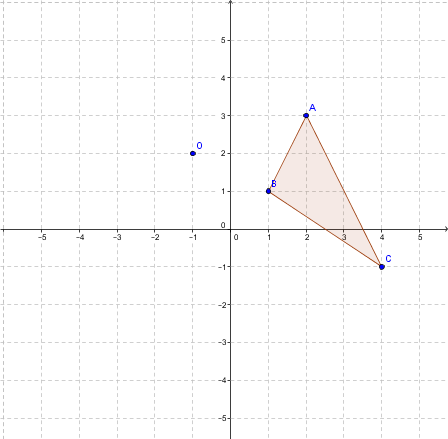
Les sommets de la figure initiale sont:
|A(2,3)|;
|B(1,1)|;
|C(4,-1)|.
On doit translater chacun des points pour ramener le centre de rotation à |(0,0)|. On obtient la règle |t_{(1,-2)}:(x,y) \mapsto (x+1,y-2)|.
On obtient les points:
|A(2,3) \mapsto (3,1)=A'|;
|B(1,1) \mapsto (2,-1)=B'|;
|C(4,-1) \mapsto (5,-3)=C'|.
On obtient la figure en rouge.
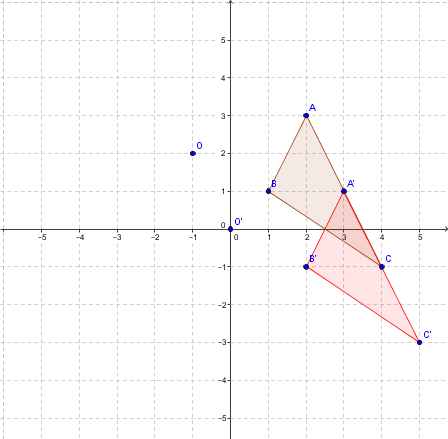
On effectue la rotation de centre |O'| et d'angle |90°| dans le sens antihoraire.
On utilise la règle |r_{(O,90°)}:(x,y) \mapsto (-y,x)|.
On obtient alors les points:
|A'(3,1) \mapsto (-1,3)=A''|;
|B'(2,-1) \mapsto (1,2)=B''|;
|C'(5,-3) \mapsto (3,5)=C''|.
On obtient alors la figure en bleu.
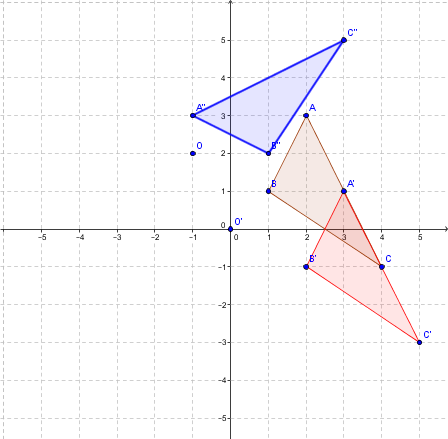
Il ne reste qu'à faire la translation inverse, c'est-à-dire |t_{(-1,2)}:(x,y) \mapsto (x-1,y+2)|.
On obtient alors les points:
|A''(-1,3) \mapsto (-2,5)=A'''|;
|B''(1,2) \mapsto (0,4)=B'''|;
|C''(3,5) \mapsto (2,7)=C'''|.
On obtient alors le résultat final, celui-ci est représenté par le triangle rose.
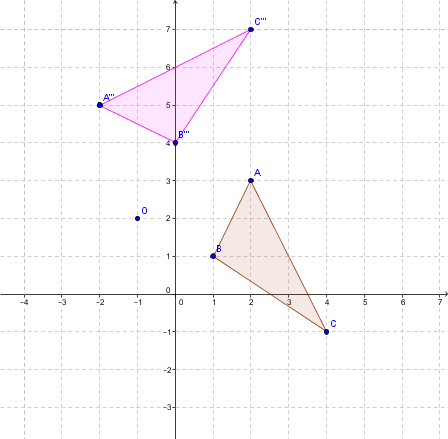
Exemple de rotation
Le triangle rose est la figure initiale.

On compare les coordonnées des sommets homologues :
|A| et |A’|: |(2 , 3)| et |(-3 , 2)|;
|B| et |B’|: |(3 , 2)| et |(-2 , 3)|;
|C| et |C’|: |(1 , 1)| et |( -1 , 1)|.
On remarque que l'ordre des coordonnées a été inversé et que le |y| du début a changé de signe : |(x , y) \mapsto (-y , x)|.
Ces changements correspondent à ceux d'une rotation de |90°| ou de |-270°|.
ATTENTION : En regardant le dessin, on pourrait croire à une symétrie par rapport à l’axe des ordonnées, mais ce n’est pas le cas. Il est très important de bien identifier les sommets homologues.