Modelling a simple interest rate is very similar to modelling a first-degree (linear) function.
It is essential to be able to change a number from a percentage to decimal notation.
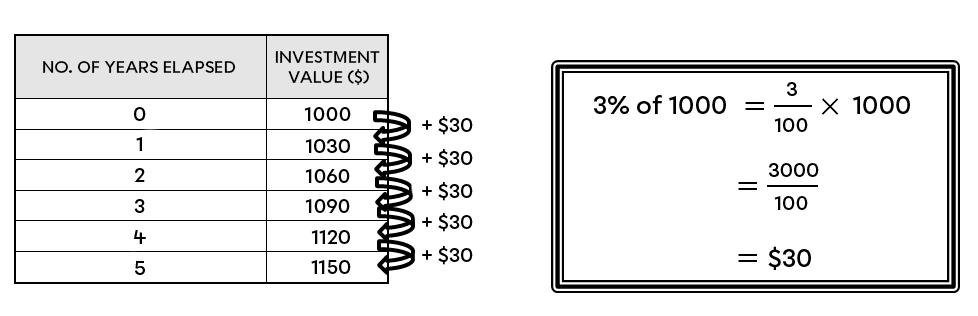
An interest rate written in decimal notation, denoted by |i,| is considered simple if it is always calculated as a function of the same amount of money, namely the initial amount.
This means that the rate of change is always constant over time (partial variation function), since the initial amount and the interest rate do not vary.
If |\$1000| is invested at a simple interest rate of |3 \%| for a period of |5| years, the following return is obtained:
In some cases, interest rates can exponentially impact loans, investments or stocks. Such is the case with compound interest rates.
Remember, this type of modelling follows a first-degree linear function. Financially speaking, this means that interest is always calculated from the original amount. At the end of each period, the interest earned during the period is not added to the initial capital for the next time annual interest is calculated.
The interest rate is annual, but often capitalization is also performed on an annual basis. In other words, the interest is only calculated once a year.
What is the graph of an investment of |\color{#ec0000}{\$3000}| with a simple interest rate of |3.25 \%| over a 3-year period?
-
Calculate the amount obtained after each interest period.||\begin{align}3.25\%\ \text{of}\ \color{#ec0000}{3000} &= 3.25\% \times \color{#ec0000}{3000} \\ &= 0.0325 \times \color{#ec0000}{3000} \\ &= \color{#3b87cd}{\$\,97.50}\end{align}||
-
Create a table of values.
||\begin{align}\begin{gathered}\text{Time elapsed}\\ \text{(years)}\end{gathered} &\ \begin{gathered}\ \ \text{Investment} \\ \ \text{value}\ (\$)\end{gathered} \\[5pt]0\qquad \ &\qquad\ \color{#ec0000}{3000} \\&&\!\!\!\!\!\!\! +\color{#3b87cd}{97.50} \\1\qquad \ &\qquad\ 3097.50 \\&&\!\!\!\!\!\!\! +\color{#3b87cd}{97.50} \\2\qquad \ &\qquad\ 3195 \\&&\!\!\!\!\!\!\! + \color{#3b87cd}{97{,}50} \\3\qquad \ &\qquad\ 3292.50 \end{align}||
-
Draw the graph.
This graph, illustrating the value of the investment according to the number of years, includes the time elapsed, in years, on the x-axis and the value of the investment, in dollars, on the y-axis.
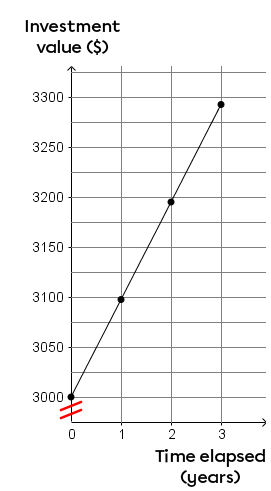
The points are perfectly aligned when connected. This means we can derive the rule from the graph.
||\begin{align} y &= \color{#3b87cd}{a} x + \color{#ec0000}{b} \\[2pt] \text{Future value} &= \color{#3b87cd}{\$ \ \text{from one interest period}} \times n + \color{#ec0000}{\text{Present value}}\\[2pt] C_n &= \color{#3b87cd}{C_0 \times i} \times n + \color{#ec0000}{C_0}\\[2pt] C_n &= C_0 (i \times n + 1)\end{align}||where
|C_n :| Future value (Accrued capital)
|C_0 :| Present Value (Initial capital)
|i :| Annual simple interest rate in decimal notation
|n :| Number of interest periods (duration)
Once we have identified the rule, we can use it to calculate the capitalization (future value) after a specific period.
What is the future value of a |\color{#ec0000}{\$3000 }| investment with a simple interest rate of |\color{#3b87cd}{3.25\%}| over a period of |\color{#ff55c3}{10}| years?
-
Find the rule.||\begin{align} C_n &= \color{#ec0000}{C_0} ({\color{#3b87cd}{i}} \times {\color{#ff55c3}{n}} + 1) \\ C_n &= \color{#ec0000}{3000} ({\color{#3b87cd}{0.0325}} \times {\color{#ff55c3}{n}} + 1)\end{align}||
-
Calculate the future value according to the given time period.||\begin{align} C_n &= 3000 ({0.0325} \times {\color{#ff55c3}{n}} + 1) \\ &= 3000 (0.0325\times \color{#ff55c3}{10} + 1) \\ &= 3000 (1.325) \\ &= 3975\end{align}||
-
Interpret the answer.
After a period of 10 years, the present value of |C_0 = \$3000| will have a future value of |C_n=\$3975.|
As mentioned in the Rule section above, the variable |n| is associated with the number of interest periods.
It is important to remember this distinction when working with interest periods that are not annual.
In general, the following terms are used to define the different interest periods.
| Period | Definition | Fraction of a year |
|---|---|---|
| Daily | Once a day | |\dfrac{1}{365}| |
| Weekly | Once a week | |\dfrac{1}{52}| |
| Monthly | Once a month | |\dfrac{1}{12}| |
| Quarterly | Once every 3 months | |\dfrac{1}{4}| |
| Semi-annually | Once every 6 months | |\dfrac{1}{2}| |
Sometimes, interest rates are linked to these periods, so pay special attention to the number of interest periods (duration) in the calculations.
What is the future value of a |\color{#ec0000}{\$5000}| investment with a quarterly simple interest rate of |\color{#3b87cd}{1.5 \%}| over a period of |\color{#ff55c3}{5}| years?
-
Find the rule.||\begin{align} C_n &= \color{#ec0000}{C_0} \left({\color{#3b87cd}{i}} \times {\color{#ff55c3}{n}} + 1\right) \\ C_n &= \color{#ec0000}{5000} \left({\color{#3b87cd}{0.015}} \times {\color{#ff55c3}{n}} + 1 \right) \end{align}||
-
Determine the number of interest periods.||\begin{align} \begin{gathered}\text{quarterly}\\ \text{for 5 years}\end{gathered} &=\begin{gathered} \text{4 times a year}\\ \text{for 5 ans}\end{gathered}\\[3pt] &= 4 \times 5 \\ &= 20\end{align}||
-
Calculate the future value according to the given period.||\begin{align}C_n &= 5000 \left({0.015} \times{\color{#ff55c3}{n}} + 1\right) \\&= 5000 \left({0.015} \times{\color{#ff55c3}{20}} + 1\right) \\&= 5000 \left(0.3 + 1 \right)\\&= 5000 \left(1.3 \right)\\&= 6500\end{align}||
-
Interpret the answer.
After a period of |5| years, the present value of |C_0 = \$5000| will have a future value of |C_n=\$6500.|
Sometimes the interest rates associated with these periods are calculated using the current annual rate. Even if the interest period is changed, the formula for calculating the future value only changes slightly.||C_n = C_0 \left(\dfrac{i}{k}\times n+1\right)||
where
|C_n:| Future value (Accrued capital
|C_0:| Present value (Initial capital)
|i:| Annual simple interest rate in decimal notation
|k:| Factor related to the interest period
|n:| Number of interest periods (Duration)
Here is an example of how to apply this formula:
What is the future value of a |\color{#ec0000}{\$3000}| investment of with an annual simple interest rate of |\color{#3b87cd}{3.25 \%}| over a period of |\color{#ff55c3}{10}| years with a semi-annual interest period?
-
Find the rule.||\begin{align}C_n &= \color{#ec0000}{C_0} \left(\dfrac{\color{#3b87cd}{i}}{\color{#fa7921}{k}} \times {\color{#ff55c3}{n}} + 1\right) \\ C_n &= \color{#ec0000}{3000} \left(\dfrac{\color{#3b87cd}{0.0325}}{\color{#fa7921}{2}} \times {\color{#ff55c3}{n}}+ 1\right)\end{align}||
-
Determine the number of interest periods.||\begin{align} \begin{gathered}\text{semi-annually}\\ \text{for 10 years}\end{gathered} &=\begin{gathered} \text{twice a year}\\ \text{for 10 years}\end{gathered}\\[3pt] &= 2 \times 10 \\ &= 20\end{align}||
-
Calculate the future value according to the given period.||\begin{align}C_n &= 3000 \left(\dfrac{0.0325}{2} \times {\color{#ff55c3}{n}}+ 1\right) \\&= 3000 \left(\dfrac{0.0325}{2}\times \color{#ff55c3}{20} + 1\right) \\&= 3000 \left(0.325 + 1 \right)\\&= 3975\end{align}||
-
Interpret the answer.
After a period of |10| years, the current value of |C_0 = \$3000| has a future value of |C_n=\$3975.|
As proven prior, the interest period has no impact on the future value when the interest is simple. This can be attributed to the fact that calculating simple interest is modelled by a first-degree linear function.
||C_n = C_0 \left (i \times n +1 \right)||where
|C_n:| Future value (Accrued capital)
|C_0:| Present value (Initial capital)
|i:| Annual simple interest rate in decimal notation
|n:| Number of interest periods (Duration)
To celebrate his eventual retirement, Arthur plans to go on a Caribbean cruise. According to his financial advisor, he must continue working for |\color{#ff55c3}{8}| more years before he can afford his trip.
What amount should he invest today if he knows that his trip will cost |\color{#EC0000}{\$8000}| and that the investment will have an annual simple interest rate of |\color{#3b87cd}{7.5 \%}|?
-
Find the rule.||\begin{align} \color{#ec0000}{C_n} &= C_0 \left (\color{#3b87cd}{i} \times \color{#ff55c3}{n} +1 \right) \\ \color{#ec0000}{8000} &= C_0 \left(\color{#3b87cd}{0.075}\times\color{#ff55c3}{8} +1 \right) \end{align}||
-
Isolate the current value (initial capital).||\begin{align}\color{#ec0000}{8000} &= C_0 \left(\color{#3b87cd}{0.075} \times \color{#ff55c3}{8} +1 \right) \\ \dfrac{8000}{\color{#3a9a38}{1.6}} &= \frac{C_0 \left (1.6 \right)}{\color{#3a9a38}{1.6}} \\ 5000 &= C_0 \end{align}||
-
Write the answer statement.
Arthur should invest approximately |\$5000.|