En ce qui concerne le taux d'intérêt simple, sa modélisation est très similaire à une fonction polynomiale de degré 1.
Il est essentiel de pouvoir passer de l'écriture d'un pourcentage vers l'écriture d'un nombre en notation décimale.
Un taux d'intérêt écrit en notation décimale et noté |i| est dit simple si ce taux d'intérêt est toujours calculé en fonction du même montant, soit le montant initial.
Ainsi, la variation est toujours constante dans le temps (fonction de variation partielle) puisque le montant initial et le taux d'intérêt ne varient pas.
Si un montant de |1\ 000\ \$| est placé à un taux d'intérêt simple de |3\ \%| sur une durée de |5| ans, on obtient le rendement suivant.
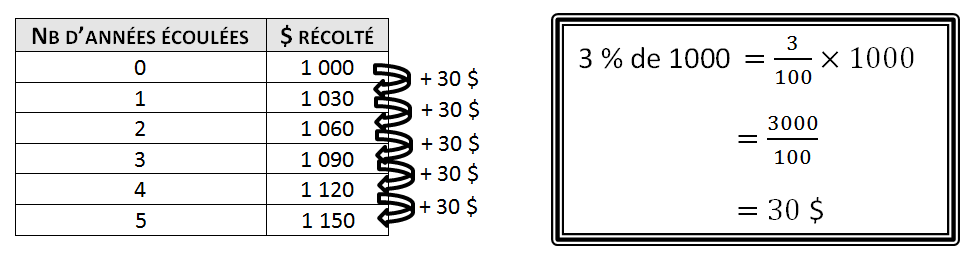
Dans certains cas, les taux d'intérêts peuvent avoir une influence exponentielle sur le prêt, le placement ou l'investissement. C'est le cas des taux d'intérêt composés.
En guise de rappel, ce type de modélisation fait référence à la fonction polynomiale de degré 1. Financièrement parlant, cela signifie que les intérêts sont toujours calculés sur le montant initial. En effet, à la fin de chaque période, les intérêts obtenus pendant celle-ci ne sont pas ajoutés au capital initial pour le prochain calcul des intérêts.
Non seulement le taux d'intérêt est annuel, mais il arrive souvent que la capitalisation se fasse également annuellement. En d'autres mots, cela implique que les intérêts ne sont calculés qu'une fois par année.
Quelle est la représentation graphique d'un placement de |\color{#ec0000}{3\ 000\ \$}| avec un taux d'intérêt simple de |3{,}25\ \%| sur une période de |3| ans?
-
Calculer le montant d'intérêt obtenu après chaque période d'intérêt ||\begin{align}3{,}25\ \%\ \text{de}\ \color{#ec0000}{3\ 000} &= 3{,}25\ \% \times \color{#ec0000}{3\ 000} \\ &= 0{,}032\,5 \times \color{#ec0000}{3\ 000} \\ &= \color{#3b87cd}{97{,}50}\ \$\end{align}||
-
Construire une table des valeurs ||\begin{align}\begin{gathered}\text{Temps écoulé}\\ \text{(années)}\end{gathered} &\ \begin{gathered}\text{Valeur du} \\ \ \ \text{ placement}\ (\$)\end{gathered} \\[5pt]0\qquad \ &\qquad\ \ \color{#ec0000}{3\ 000} \\&&\!\!\!\!\!\!\! +\color{#3b87cd}{97{,}50} \\1\qquad \ &\qquad\ \ 3\ 097{,}50 \\&&\!\!\!\!\!\!\! +\color{#3b87cd}{97{,}50} \\2\qquad \ &\qquad\ \ 3\ 195 \\&&\!\!\!\!\!\!\! + \color{#3b87cd}{97{,}50} \\3\qquad \ &\qquad\ \ 3\ 292{,}50 \end{align}||
-
Construire le graphique
Ce graphique, illustrant la valeur du placement selon le nombre d'années, comprend le nombre d'années en axe des abscisses et la valeur du placement, en dollars, sur l'axe des ordonnées.
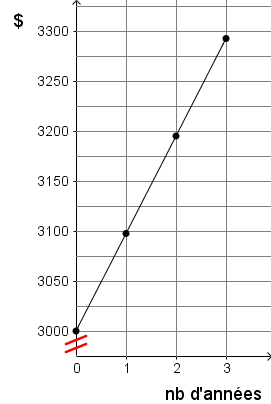
En reliant les points, on s'aperçoit qu'ils sont parfaitement alignés. Ainsi, on peut déduire la règle d'une telle représentation graphique.
||\begin{align} y &= \color{#3b87cd}{a} x + \color{#ec0000}{b} \\[2pt] \text{Valeur future} &= \color{#3b87cd}{\$ \ \text{d'une période d'intérêt}} \times n + \color{#ec0000}{\text{Valeur actuelle}}\\[2pt] C_n &= \color{#3b87cd}{C_0 \times i} \times n + \color{#ec0000}{C_0}\\[2pt] C_n &= C_0 (i \times n + 1)\end{align}||
où
|C_n :| Valeur future (Capital accumulé)
|C_0 :| Valeur actuelle (Capital initial)
|i :| Taux d'intérêt simple annuel en notation décimale
|n :| Nombre de périodes d'intérêt (durée)
Une fois la règle trouvée, on peut l'utiliser pour calculer la capitalisation suite à une période précise.
Quelle serait la valeur future d'un placement de |\color{#ec0000}{3\ 000\ \$}| avec un taux d'intérêt simple de |\color{#3b87cd}{3{,}25\ \%}| sur une période de |\color{#ff55c3}{10}| ans?
-
Trouver la règle ||\begin{align} C_n &= \color{#ec0000}{C_0} ({\color{#3b87cd}{i}} \times {\color{#ff55c3}{n}} + 1) \\ C_n &= \color{#ec0000}{3\ 000} ({\color{#3b87cd}{0{,}032\,5}} \times {\color{#ff55c3}{n}} + 1) \end{align}||
-
Calculer la valeur future selon la période donnée ||\begin{align} C_n &= 3\ 000 ({0{,}032\,5} \times {\color{#ff55c3}{n}} + 1) \\ &= 3\ 000 (0{,}032\,5\times \color{#ff55c3}{10} + 1) \\ &= 3\ 000 (1{,}325) \\ &= 3\ 975\end{align}||
-
Interpréter la réponse
Après une période de 10 ans, la valeur actuelle |C_0 = 3\ 000\ \$| est devenue une valeur future |C_n=3\ 975 \ \$.|
Comme il est précisé dans l'encadré Règle plus haut, la valeur associée à la variable |n| doit vraiment correspondre au nombre de périodes d'intérêt.
Une telle distinction est digne de mention lorsque vient le temps de travailler avec des périodes d'intérêt qui ne sont pas annuelles.
De façon générale, les termes suivants sont utilisés pour définir les différentes périodes d'intérêt.
| Période | Définition | Fraction d'une année |
|---|---|---|
| Quotidienne | Une fois par jour | |\dfrac{1}{365}| |
| Hebdomadaire | Une fois par semaine | |\dfrac{1}{52}| |
| Mensuelle | Une fois par mois | |\dfrac{1}{12}| |
| Trimestrielle | Une fois tous les 3 mois | |\dfrac{1}{4}| |
| Semestrielle | Une fois tous les 6 mois | |\dfrac{1}{2}| |
Il arrive que les taux d'intérêt soient en lien avec ces périodes. Il faudra donc porter une attention particulière aux nombres de périodes d'intérêt (durée) lors des calculs.
Quelle serait la valeur future d'un placement de |\color{#ec0000}{5\ 000\ \$}| avec un taux d'intérêt simple trimestriel de |\color{#3b87cd}{1{,}5\ \%}| sur une période de |\color{#ff55c3}{5}| ans?
-
Trouver la règle||\begin{align} C_n &= \color{#ec0000}{C_0} \left({\color{#3b87cd}{i}} \times {\color{#ff55c3}{n}} + 1\right) \\ C_n &= \color{#ec0000}{5\ 000} \left({\color{#3b87cd}{0{,}015}} \times {\color{#ff55c3}{n}} + 1 \right) \end{align}||
-
Déterminer le nombre de périodes d'intérêt||\begin{align} \begin{gathered}\text{trimestriel}\\ \text{pendant 5 ans}\end{gathered} &=\begin{gathered} \text{4 fois par année}\\ \text{pendant 5 ans}\end{gathered}\\[3pt] &= 4 \times 5 \\ &= 20\end{align}||
-
Calculer la valeur future selon la période donnée||\begin{align}C_n &= 5\ 000 \left({0{,}015} \times {\color{#ff55c3}{n}} + 1\right) \\ &= 5\ 000 \left({0{,}015} \times {\color{#ff55c3}{20}} + 1\right) \\&= 5\ 000 \left(0{,}3 + 1 \right)\\ &= 5\ 000 \left(1{,}3 \right)\\ &= 6\ 500\end{align}||
-
Interpréter la réponse
Après une période de |5| ans, la valeur actuelle |C_0 = 5\ 000\ \$| est devenue une valeur future |C_n=6\ 500 \ \$.|
Parfois, les taux d'intérêt en lien avec ces périodes sont calculés selon le taux annuel en vigueur. Même si la période d'intérêt est modifiée, la formule pour déterminer la valeur future ne subit qu'une légère modification. ||C_n = C_0 \left(\dfrac{i}{k}\times n+1\right)||
où
|C_n :| Valeur future (Capital accumulé)
|C_0 :| Valeur actuelle (Capital initial)
|i :| Taux d'intérêt simple annuel en notation décimale
|k :| Facteur en lien avec la période d'intérêt
|n :| Nombre de périodes d'intérêt (Durée)
Voici un exemple de l'application de cette formule.
Quelle serait la valeur future d'un placement de |\color{#ec0000}{3\ 000\ \$}| ayant un taux d'intérêt simple annuel de |\color{#3b87cd}{3{,}25\ \%}| sur une période de |\color{#ff55c3}{10}| ans avec une période d'intérêt semestrielle?
-
Trouver la règle||\begin{align}C_n &= \color{#ec0000}{C_0} \left(\dfrac{\color{#3b87cd}{i}}{\color{#fa7921}{k}} \times {\color{#ff55c3}{n}} + 1\right) \\ C_n &= \color{#ec0000}{3\ 000} \left(\dfrac{\color{#3b87cd}{0{,}032\,5}}{\color{#fa7921}{2}} \times {\color{#ff55c3}{n}}+ 1\right)\end{align}||
-
Déterminer le nombre de périodes d'intérêt||\begin{align} \begin{gathered}\text{semestrielle}\\ \text{pendant 10 ans}\end{gathered} &=\begin{gathered} \text{2 fois par année}\\ \text{pendant 10 ans}\end{gathered}\\[3pt] &= 2 \times 10 \\ &= 20\end{align}||
-
Calculer la valeur future selon la période donnée||\begin{align}C_n &= 3\ 000 \left(\dfrac{0{,}032\,5}{2} \times {\color{#ff55c3}{n}}+ 1\right) \\&= 3\ 000 \left(\dfrac{0{,}032\ 5}{2}\times \color{#ff55c3}{20} + 1\right) \\&= 3\ 000 \left(0{,}325 + 1 \right)\\&= 3\ 975\end{align}||
-
Interpréter la réponse
Après une période de |10| ans, la valeur actuelle |C_0 = 3\ 000\ \$| est devenue une valeur future |C_n=3\ 975\ \$.|
Comme il a été démontré plus tôt, la période d'intérêt n'a aucun impact sur la valeur future lorsque l'intérêt est simple. On peut lier cette déduction au fait que le calcul d'un intérêt simple est modélisé par la fonction polynomiale de degré 1.
||C_n = C_0 \left(i \times n +1 \right)||
où
|C_n:| Valeur future (Capital accumulé)
|C_0:| Valeur actuelle (Capital initial)
|i:| Taux d'intérêt simple annuel en notation décimale
|n:| Nombre de périodes d'intérêt (Durée)
Afin de fêter le début de sa retraite, Arthur prévoit aller faire une croisière dans la mer des Caraïbes. Selon son conseiller financier, il doit demeurer sur le marché du travail pour les |\color{#ff55c3}{8}| prochaines années avant d'être financièrement capable de réaliser son voyage.
Ainsi, quel montant doit-il investir aujourd'hui s'il sait que son voyage lui coutera |\color{#ec0000}{8\ 000 \ \$}| et que le tout sera soumis à un taux d'intérêt simple annuel de |\color{#3b87cd}{7{,}5\ \%}|?
-
Trouver la règle||\begin{align} \color{#ec0000}{C_n} &= C_0 \left (\color{#3b87cd}{i} \times \color{#ff55c3}{n} +1 \right) \\ \color{#ec0000}{8\ 000} &= C_0 \left(\color{#3b87cd}{0{,}075}\times\color{#ff55c3}{8} +1 \right) \end{align}||
-
Isoler la valeur actuelle (capital initial)||\begin{align}\color{#ec0000}{8\ 000} &= C_0 \left(\color{#3b87cd}{0{,}075} \times \color{#ff55c3}{8} +1 \right) \\ \dfrac{8\ 000}{\color{#3a9a38}{1{,}6}} &= \frac{C_0 \left (1{,}6 \right)}{\color{#3a9a38}{1{,}6}} \\ 5\ 000 &= C_0 \end{align}||
-
Donner la réponse dans une phrase
Ainsi, la valeur actuelle du placement d'Arthur doit être d'environ |5\ 000\ \$.|