Compound interest allows your assets to grow faster than simple interest. Unfortunately, debts also grow faster with a compound interest rate.
An interest rate written in decimal notation, denoted by |i,| is compounded if the interest is calculated based on an initial amount plus the interest accrued at the end of each capitalization period.
As a result, the amount to which interest is applied will increase more and more rapidly over time. Simply put, compound interest can be modelled by an exponential function.
If an amount of |\$1000| is invested at a |3\%| interest rate compounded annually for a period of |5| years, the following return will be obtained:
| Number of years elapsed | Annual return ($) | Capital ($) |
|---|---|---|
| |0| | - | |1000| |
| |1| | |3 \%| of |1000 = 30| | |1000 + 30 = 1030| |
| |2| | |3 \%| of |1030 = 30.90| | |1030 + 30.90 = 1060.90| |
| |3| | |3 \%| of | 1060.90 \approx 31.83| | |1060.90 + 31.83 = 1092.73| |
| |4| | |3 \%| of |1092.73 \approx 32.78| | |1092.73 + 32.78 = 1125.51| |
| |5| | |3 \%| of |1125.51 \approx 33.77| | |1125.51 + 33.77 = 1159.28| |
Therefore, the amount earned after |5| years will be about |\$1159.28.|
Again, this type of modelling is based on the exponential function. Financially speaking, this means that the interest is always calculated on the accumulated capital from the previous interest period.
Not only is the interest rate annual, but often the interest period is also measured in years. In other words, the interest is only calculated once a year.
What is the graph of a |\color{red}{\$3000}| investment with a compound interest rate of |3.25 \%| over a 2-year period?
-
Calculate the interest earned for each interest period.
||\begin{align}\small{\text{No. of years elapsed}} &&& \small{\$ \ \text{earned}} \\0 &&& \color{red}{3000} \\&&&&& \small{+ \ 3.25\% \ \text{of} \ 3000 =\color{blue}{97.50}} \\1 &&& 3097.50 \\&&&&& \small{+ \ 3.25\% \ \text{of} \ 3097.50 \approx \color{blue}{100.67}} \\2 &&& 3198.17 \end{align}||
-
Sketch the graph
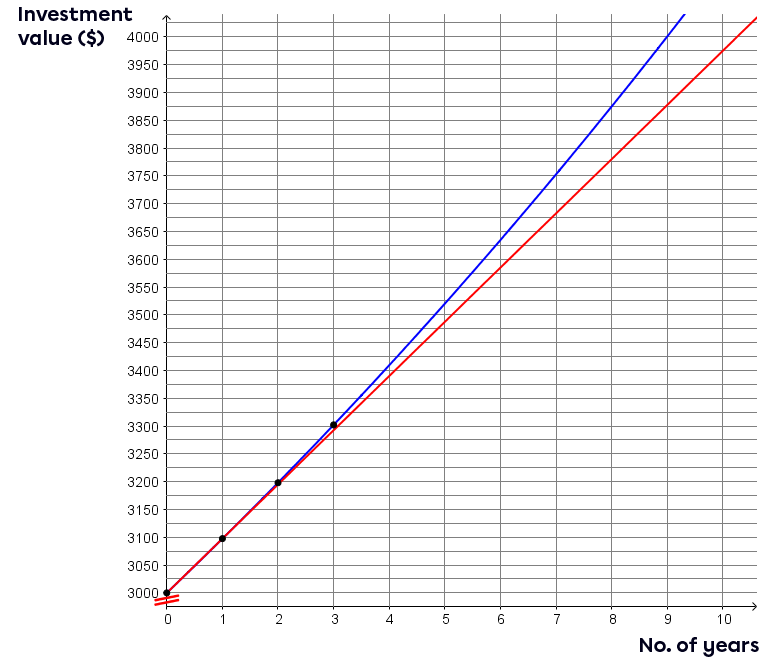
In the last example, the straight red line represents the calculation of simple interest. The blue curved line, on the other hand, represents the calculation of compound interest. It can be seen that compound-interest investment returns create more capital in the long term.
Using the previous example, we can find the rule from such a graph.
||C_n=C_0 \ \left(1+i \right)^n||
where
|C_n:| Future value (Accrued capital)
|C_0:| Present value (Initial capital)
|i :| Annual compound interest rate in decimal notation
|n :| Number of interest periods (Duration)
To understand the origin of this rule, factoring and exponential notation are used.
|\begin{align} 3198.17 &= \underbrace{\color{#3b87cd}{3000}}_{\text{Present value}} + \underbrace{\color{#3b87cd}{3000 \times 0.0325}}_{\text{Interest after 1 year}} + \underbrace{(3000+3000\times 0.0325)\times 0.0325}_{\text{Interest after 2 years}} \\ &= \underbrace{\color{#3b87cd}{3000 (1 + 0.0325)}}_{\text{Factoring out 3000}} + (3000 + 3000 \times 0.0325) \times 0.0325\\ &= \color{#3b87cd}{3000 (1 + 0.0325)}+ \underbrace{(\color{#3b87cd}{3000 (1 + 0.0325)})}_{\text{Factoring out 3000}} \times 0.0325 \\ &= \underbrace{\color{#3b87cd}{3000 (1 + 0.0325)}}_{\text{Factoring}} (1+0.0325)\\ 3198.17&= 3000\!\! \underbrace{(1 + 0.0325)^2}_{\text{Definition of an exponent}}\end{align}|
Generalizing gives the rule:
|\qquad C_n = C_0 \ \left(1 + i \right)^n|
Once we have found the rule, we can use it to calculate any future value after a specific time period.
What is the future value of a |\color{#ec0000}{\$3000}| investment with an annual compound interest rate of |\color{#3b87cd}{3.25 \%}| over a period of |\color{#ff55c3}{10}| years?
-
Find the rule.||\begin{align}C_n &= \color{#ec0000}{C_0} \ \left(1 + \color{#3b87cd}{i} \right)^ \color{#ff55c3}{n} \\ &= \color{#ec0000}{3000} \ \left(1 + \color{#3b87cd}{0.0325} \right)^\color{#ff55c3}{n}\end{align}||
-
Calculate the future value according to the given time period.||\begin{align}C_n &= 3000 \ \left(1 + 0.0325\right)^\color{#ff55c3}{n}\\ &= 3000 \ \left(1.0325 \right)^\color{#ff55c3}{10} \\ &\approx 3000 (1.37689) \\ &\approx 4130.68 \end{align}||
-
Interpret the answer.
After a period of |10| years, the present value |C_0 = \$3000| has a future value of |C_n\approx \$4130.68.|
The formula used to calculate the future value simply involves dividing the annual interest rate by the given interest period.
In general, the following terms are used to define the different interest periods.
|
Period |
Definition |
Fraction of a year |
|---|---|---|
|
Daily |
Once a day |
|\dfrac{1}{365}| |
|
Weekly |
Once a week |
|\dfrac{1}{52}| |
|
Monthly |
Once a month |
|\dfrac{1}{12}| |
|
Quarterly |
Once every 3 months |
|\dfrac{1}{4}| |
|
Semi-annually |
Once every 6 months |
|\dfrac{1}{2}| |
Sometimes, interest rates are linked to these periods, so pay special attention to the number of interest periods (duration) in your calculations.
What is the future value of a |\color{#ec0000}{\$5000}| investment with an interest rate of |\color{#3b87cd}{1.5 \%}| compounded quarterly over a period of |\color{#ff55c3}{5}| years?
-
Find the rule.||\begin{align}C_n &= \color{#ec0000}{C_0} \ \left(1 + \color{#3b87cd}{i} \right)^\color{#ff55c3}{n} \\&= \color{#ec0000}{5000} \ \left(1 + \color{#3b87cd}{0.015} \right)^\color{#ff55c3}{n}\end{align}||
-
Determine the number of interest periods.||\begin{align} \begin{gathered}\text{quarterly}\\ \text{for 5 years}\end{gathered} &=\begin{gathered} \text{4 times a year}\\ \text{for 5 years}\end{gathered}\\[3pt] &= 4 \times 5 \\ &= 20\end{align}||
-
Calculate the future value according to the given time period.||\begin{align}C_n&= 5000 \ \left(1 + 0.015 \right)^\color{#ff55c3}{n}\\&= 5000 \ \left(1 + 0.015 \right)^\color{#ff55c3}{20}\\&= 5000 \ \left (1.015 \right)^{20} \\&\approx 6734.28 \end{align}||
-
Interpret the answer.
After a period of |5| years, the present value |C_0 = \$5000| has a future value of |C_n\approx \$6734.28.|
Sometimes the interest rates associated with these periods are calculated at the current annual rate. Even if the interest period is modified, the formula for calculating the future value is only slightly changed.||C_n=C_0 \ \left(1+\frac{i}{k}\right)^n||
where
|C_n:| Future value (Accrued capital)
|C_0:| Present value (Initial capital)
|i:| Annual compound interest rate in decimal notation
|k:| Factor related to the interest period
|n :| Number of interest periods (Duration)
By referring to the vocabulary associated with interest periods, we can see that compound interest has a considerable effect on future value.
Here is an example of how to apply this formula:
What is the future value of a |\color{#ec0000}{\$3000}| investment with an annual interest rate of |\color{#3b87cd}{3.25 \%}| compounded monthly over a period of |\color{#ff55c3}{10}| years?
-
Find the rule.||\begin{align} C_n &= \color{#ec0000}{C_0} \ \left(1 + \dfrac{\color{#3b87cd}{i}}{\color{#fa7921}{k}} \right)^\color{#ff55c3}{n} \\ &= \color{#ec0000}{3000} \ \left(1 + \dfrac{\color{#3b87cd}{0.0325}}{\color{#fa7921}{12}} \right)^\color{#ff55c3}{n}\end{align}||
-
Determine the number of interest periods.||\begin{align} \begin{gathered}\text{monthly}\\ \text{for 10 years}\end{gathered} &=\begin{gathered} \text{12 times a year}\\ \text{for 10 years}\end{gathered}\\[3pt] &= 12 \times 10 \\ &= 120\end{align}||
-
Calculate the future value according to the given time period.||\begin{align}C_n &= 3000 \ \left(1 + \frac{0.0325}{12} \right)^\color{#ff55c3}{n}\\&= 3000 \ \left(1 + \frac{0.0325}{12} \right)^\color{#ff55c3}{120}\\&\approx 3000 \ \left (1.0027 \right)^{120} \\&\approx 4150.27 \end{align}||
-
Interpret the answer.
After a period of |10| years, the current value |C_0 = \$3000| has a future value of |C_n\approx \$4150.27.|
Sometimes, investors place their investments with the goal of obtaining a specific final amount. In other words, the future value (accrued capital) and the duration of the investment (number of interest periods) are known, but the current value (initial capital) is unknown. This is the inverse operation of capitalization (calculating future value).
Since the starting value (initial capital) is unknown, this present value must be found.
Compound interest makes algebraic operations a little more complex. The presence of an exponent requires using the laws of exponents.
When solving any type of equation, inverse operations are used to isolate a variable.
After his third child is born, Vincent wants to put money aside to pay for his son’s future education expenses. According to the information available, the average cost of a university education is |\color{#ec0000}{\$60\ 000}.|
Assuming that this money is needed in |\color{#ff55c3}{23}| years, how much should Vincent invest if the plan he is using has a monthly compound interest rate of |\color{#3b87cd}{0.2 \%}|?
-
Find the rule.||\begin{align} \color{#ec0000}{C_n} &= C_0 \ \left(1+{\color{#3b87cd}{i}} \right)^{\color{#ff55c3}{n}} \\ \color{#ec0000}{60 \ 000} &= C_0 \ \left(1+{\color{#3b87cd}{0.002}} \right)^{\color{#ff55c3}{12 \times 23}} \\ \color{#ec0000}{60 \ 000} &= C_0 \ \left(1+{\color{#3b87cd}{0.002}} \right)^{\color{#ff55c3}{276}}\end{align}||
-
Isolate the current value (initial capital).||\begin{align} \color{#ec0000}{60\ 000} &= C_0 \ \left(1+{\color{#3b87cd}{0.002}} \right)^{\color{#ff55c3}{276}} \\ \color{#ec0000}{60\ 000} &= C_0 \ \left(1.002 \right)^{\color{#ff55c3}{276}} \\ \dfrac{\color{#ec0000}{60\ 000}}{\color{#3a9a38}{1.7358}} &\approx \dfrac{C_0 \left(1.7358 \right)}{\color{#3a9a38}{1.7358}} \\ 34\ 566.87 &\approx C_0 \end{align}||
-
State the answer as a sentence.
Arthur should invest about |\$34\ 566.87.|
To avoid calculation errors, we can derive a formula from this procedure.
||C_0 = C_n \ \left(1+{i} \right)^{-n}||
where
|C_0 :| Present value (Initial capital)
|C_n :| Future value (Accrued capital)
|i :| Annual compound interest rate in decimal notation
|n :| Number of interest periods (Duration)
Ainsi, la démarche est plus concise.
With all her investments, Gitane forgot the current value of one of them. She has the following information:
-
it is an investment with a weekly compound interest rate of |0.04\%|
-
this investment has a total duration of |5| years
-
the future value (accrued capital) obtained will be: |\$4660.23|
What is the current value (initial capital) of this investment?
-
Identify the information provided.||\begin{align} \color{#ec0000}{C_n} &= \color{#ec0000}{4660.23} \\ \color{#3b87cd}{i} &= \color{#3b87cd}{0.04 \ \%} = \color{#3b87cd}{0.0004} \\ \color{#ff55c3}{n} &= \color{#ff55c3}{5 \times 52 = 260}\end{align}||
-
Apply the formula.||\begin{align} C_0 &= {\color{#ec0000}{C_n}}{\left(1+{\color{#3b87cd}{i}}\right)^\color{#ff55c3}{-n}} \\ &= {\color{#ec0000}{4660.23}}{\left(1+{\color{#3b87cd}{0.0004}}\right)^\color{#ff55c3}{-260}} \\ &\approx 4200.00 \end{align}||
-
State the answer as a sentence.
The present value of Gitane’s investment is about |\$4200.00.|
Like many formulas in mathematics, this one can be proven arithmetically.
Like when modelling, the current value can be found using the following formula:
||C_n=C_0 \ \left(1+\dfrac{i}{k}\right)^n||
where
|C_n :| Future value (Accrued capital)
|C_0 :| Present value (Initial capital)
|i :| Annual compound interest rate in decimal notation
|k :| Interest period factor
|n :| Number of interest periods (Duration)