A rational equation or inequality contains a variable that appears at least once in the denominator.
Since it is impossible to divide by |0,| restrictions must be placed on the variable so that the denominator of the rational fraction is not equal to |0.|
These restrictions must be set before solving the rational equation.
Here are the steps to follow to solve a rational equation.
-
Isolate the fraction.
-
Calculate the restrictions.
-
Perform cross-multiplication.
-
Solve the equation.
-
Verify the solution(s).
-
Write the solution(s).
The cross-multiplication technique, also called the cross-product or product of extremes and means technique, is a quick and effective strategy to solve rational equations. We can also apply inverse operations to obtain the same result.
Solving a rational equation
using cross-multiplication
||\begin{align}\dfrac{4x-5}{3x}&=7\\\dfrac{\color{#FA7921}{4x-5}}{\color{#3A9A38}{3x}}&=\dfrac{\color{#3A9A38}7}{\color{#FA7921}1}\\(\color{#FA7921}{4x-5})\times \color{#FA7921}1&=\color{#3A9A38}{3x}\times \color{#3A9A38}{7}\\4x-5&=21x\end{align}||
Solving a rational equation
using inverse operations
||\begin{align}\dfrac{4x-5}{3x}&=7\\\dfrac{4x-5}{3x}\color{#EC0000}{\times 3x}&=7\color{#EC0000}{\times 3x}\\4x-5&=21x\end{align}||
Solve the equation |\dfrac{2}{x-2}+1=5.|
-
Isolate the fraction||\begin{align}\dfrac{2}{x-2}+1&=5\\\dfrac{2}{x-2}&=4\end{align}||
-
Calculate the restrictions ||\begin{align}x-2&\neq0\\x&\neq2\end{align}||
-
Perform cross-multiplication ||\begin{align}\dfrac{\color{#FA7921}2}{\color{#3A9A38}{x-2}}&=\color{#3A9A38}4\\\color{#FA7921}2&=\color{#3A9A38}4(\color{#3A9A38}{x-2})\end{align}||
-
Solve the equation ||\begin{align}2&=4x-8\\10&=4x\\2{,}5&=x\end{align}||
-
Verify the solution
Because |2{.}5\neq 2,| the solution is valid. -
Write the solution
The equation’s solution: |\dfrac{2}{x-2}+1=5| is |x=2{.}5.|
There are two ways to verify the solution obtained.
-
Ensure that the solution respects the restriction determined in step two, as shown in the previous example.
-
Substitute the solution into the original equation. In the previous example, the variable |x| is replaced in the original equation. Next, make sure that the left-hand side is equivalent to the right-hand side.||\begin{align}\dfrac{2}{\color{#3B87CD}x-2}+1&=5\\ \dfrac{2}{\color{#3B87CD}{2{,}5}-2}+1&\stackrel{?}{=}5\\4+1&\stackrel{?}{=}5\\5&=5\end{align}||The solution is indeed valid.
Solve the equation |\dfrac{3+2x}{x}=8.|
-
Isolate the fraction
The fraction is already isolated, so move on to the next step. -
Calculate the restrictions ||x\neq 0||
-
Perform cross-multiplication ||\begin{align}\dfrac{\color{#FA7921}{3+2x}}{\color{#3A9A38}x}&=\color{#3A9A38}8\\\color{#FA7921}{3+2x}&=\color{#3A9A38}8(\color{#3A9A38}x)\end{align}||
-
Solve the equation ||\begin{align}3+2x&=8x\\3&=6x\\0{.}5&=x\end{align}||
-
Verify the solution
Because |0{.}5\neq 0,| the solution is valid. -
Write the solution
The solution of the equation |\dfrac{3+2x}{x}=8| is |x=0{.}5.|
Here is an example where the equation has no solution.
Solve the equation |\dfrac{2x+5}{x-7}=2.|
-
Isolate the fraction
The fraction is already isolated, so move on to the next step. -
Calculate the restrictions ||\begin{align}x-7&\neq0\\x&\neq7\end{align}||
-
Perform cross-multiplication ||\begin{align}\dfrac{\color{#FA7921}{2x+5}}{\color{#3A9A38}{x-7}}&=\color{#3A9A38}2\\\color{#FA7921}{2x+5}&=\color{#3A9A38}2(\color{#3A9A38}{x-7})\end{align}||
-
Solve the equation ||\begin{align}2x+5&=2x-14\\0x&=-19\\0&=-19\end{align}|| It’s necessary to stop solving at this step because there’s a false equality: |0| is not equal to |-19.| The equation has no solution.
-
Verify the solution
Since the equation has no solution, this step is optional. However, the absence of a solution can be verified using the graph of the rational function.Represent the function as follows: |f(x)=\dfrac{2x+5}{x-7}| . Then, determine for which value(s) of |x| this function is equal to |2,| in other words when |\color{#333FB1}{y=2}.| Since the asymptote of the function is |\color{#333FB1}{y=2}| , a solution (or meeting point) cannot be obtained with the function.
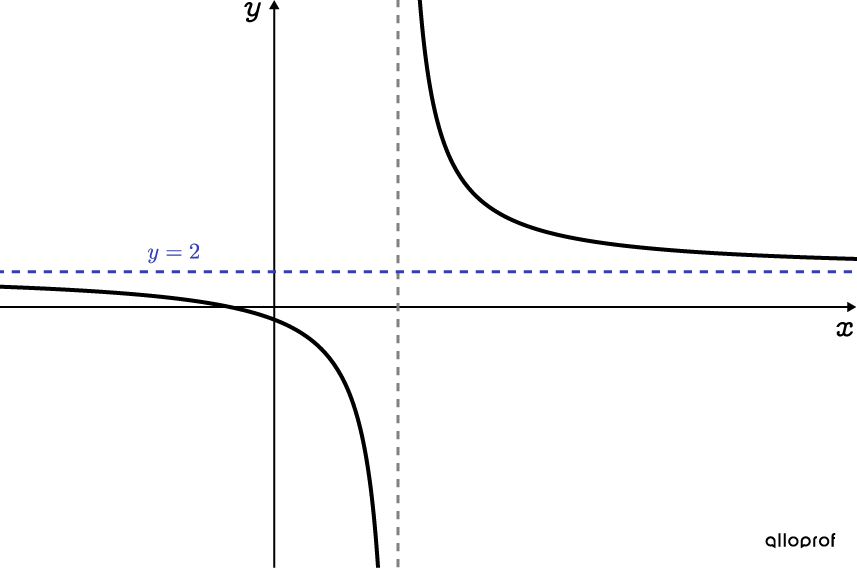
-
Write the solution set
There is no solution for the equation |\dfrac{2x+5}{x-7}=2.|
When solving a rational equation, sometimes the result is a quadratic equation. This result can mean that the equation has no solution – or it has one or two.
When these situations arise, solve a second-degree equation.
Solve the equation |\dfrac{2x+6}{x-2}=x+3.|
-
Isolate the fraction
The fraction is already isolated, so move on to the next step. -
Calculate the restrictions||\begin{align}x-2&\neq 0\\x&\neq 2\end{align}||
-
Perform cross-multiplication ||\begin{align}\dfrac{\color{#FA7921}{2x+6}}{\color{#3A9A38}{x-2}}&=\color{#3A9A38}{x+3}\\\color{#FA7921}{2x+6}&=(\color{#3A9A38}{x-2})(\color{#3A9A38}{x+3})\\2x+6&=x^2+x-6\end{align}||
-
Solve the equation
The previous step resulted in a quadratic equation. Solve it using the quadratic formula.||\begin{align}2x+6&=x^2+x-6\\0&=x^2-x-12\end{align}||||\begin{align}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\&=\dfrac{-(-1)\pm\sqrt{(-1)^2-4(1)(-12)}}{2(1)}\\\\&=\dfrac{1\pm\sqrt{49}}{2}\\\\x&\in\{-3,4\}\end{align}|| -
Verify the solutions
Since |-3\neq 2| and |4\neq 2,| the solutions are valid. -
Write the solution set
The solution set of the equation |\dfrac{2x+6}{x-2}=x+3| is |x\in\left\{-3,4\right\}.|
The solution set can be clearly seen using a graphical representation. First, draw the function |f(x)=\dfrac{2x+6}{x-2}| , then draw the line with equation |\color{#333FB1}{y=x+3}.| Since the line is oblique and not horizontal, there are two points of intersection. The |\color{#3A9A38}x| -coordinate of these points corresponds to the solutions determined in step 4.
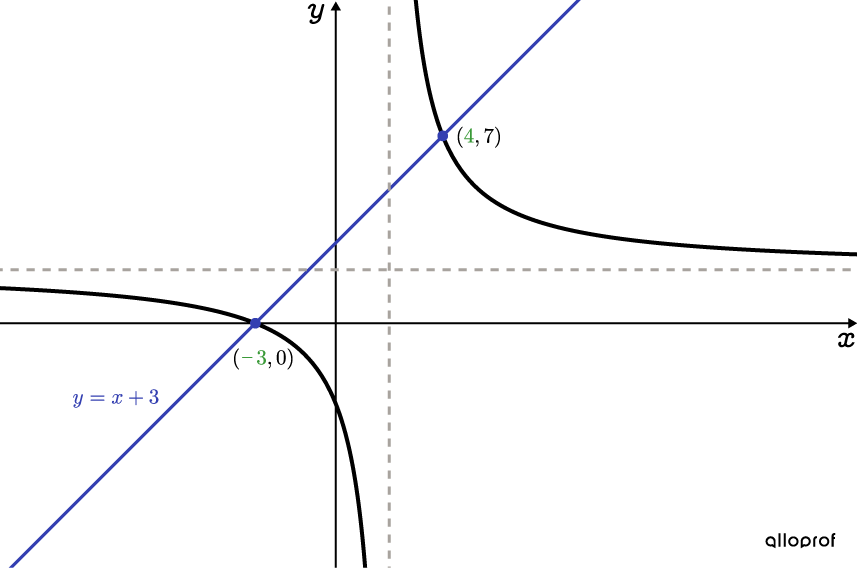
To solve a rational inequality, apply the same steps as for a rational equation.
-
Replace the inequality symbol with the equal symbol.
-
Isolate the fraction.
-
Calculate the restrictions.
-
Perform cross-multiplication.
-
Solve the equation.
-
Verify the solution of the equation.
-
Determine the solution set of the inequality using a graph or number line.
Solve the inequality |\dfrac{3}{x-1}+4\geq 6.|
-
Replace the inequality symbol with the equal symbol||\dfrac{3}{x-1}+4=6||
-
Isolate the fraction||\dfrac{3}{x-1}=2||
-
Calculate the restrictions||\begin{align}x-1&\neq 0\\x&\neq1\end{align}||
-
Perform cross-multiplication||\begin{align}\dfrac{\color{#FA7921}3}{\color{#3A9A38}{x-1}}&=\color{#3A9A38}2\\\color{#FA7921}3&=\color{#3A9A38}2(\color{#3A9A38}{x-1})\end{align}||
-
Solve the equation||\begin{align}3&=2x-2\\5&=2x\\2{.}5&=x\end{align}||
-
Verify the solution of the equation
Because |2{.}5\neq 1,| the solution is valid. -
Determine the solution set of the inequality
Draw the graph of the rational function to determine the solution set.
The vertical asymptote |x=1| corresponds to the restriction determined in step 3.
Draw the function |f(x)=\dfrac{3}{x-1}+4,| then draw a horizontal line at |\color{#333FB1}{y=6}.| This gives the coordinates of the point of intersection |(\color{#3A9A38}{2{.}5},6)| whose |\color{#3A9A38}x| coordinate corresponds to the solution determined in step 5.
We are looking for the values of |x| for which |f(x)\geq 6,| therefore, those which are greater than or equal to |6.| These values are shown in green on the following graph.
By analyzing the graph, we see that the solution set is between |1| and |2{.}5.|
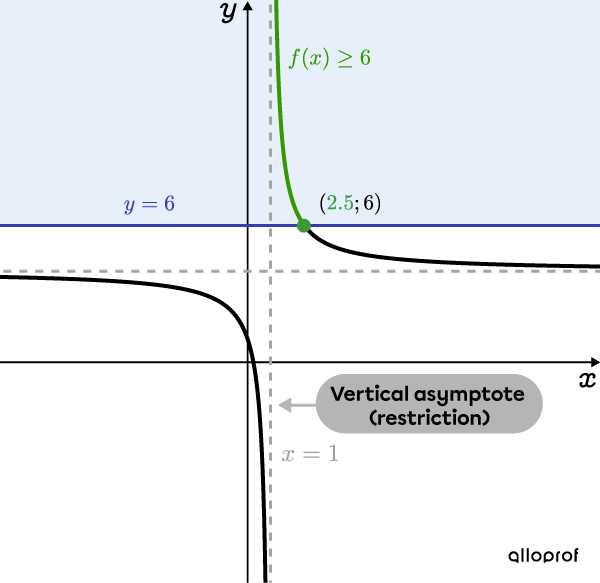
Answer: The solution set is |x\in \left]1, 2{.}5\right].|
Note: Since |x\neq 1| , it must be excluded from the answer using an open square bracket. |2{.}5| is included, since the inequality sign is |\geq| and not |>.|
The solution set (step 7) can be determined using a number line instead of a graphical representation. Using the previous example, here’s how to do it.
Place the restriction determined in step 3 on a number line. Represent it with an open point, since it is excluded from the solution set.
We also place the solution obtained in step 5. Use a solid point, since this value is included in the solution set (given that the inequality sign is |\geq| ).
|1| and |2{.}5| are called critical values.

These two values of |x| divide the number line into three intervals: |]-\infty, 1[,| |]1; 2{.}5]| , and |[2{.}5,+\infty[.| Therefore, it is necessary to verify by choosing a random value in each of these sections and plugging it into the initial inequality.
-
For |]-\infty, 1[,| use |x=0.|||\begin{align}\dfrac{3}{\color{#3B87CD}x-1}+4&\geq6\\ \dfrac{3}{\color{#3B87CD}{0}-1}+4&\stackrel{?}{\geq}6\\1&\color{#ec0000}{\not\geq}6\ \end{align}||This gives |1\color{#EC0000}{\not\geq} 6.| This conclusion shows that all values less than |1| cannot be in the solution set.
-
For |]1;2{.}5]|, use |x=2.|
This gives |7\geq 6.| Since this is true, we conclude that the interval |]1,2{.}5]| is part of the solution set. -
For |[2{.}5;+\infty[,| use |x=4.|
This gives |5\color{red}{\not \geq} 6.| The conclusion is that all values greater than |2{.}5| cannot be in the solution set.
The solution set indeed corresponds to that determined using the graph, that is, |x\in \left]1, 2{.}5\right].|
Colour the section that corresponds to the solution set on the number line.

Solve the inequality |\dfrac{-2x}{4x-5}-3<-1.|
-
Replace the inequality symbol with the equal symbol||\dfrac{-2x}{4x-5}-3=-1||
-
Isolate the fraction ||\dfrac{-2x}{4x-5}=2||
-
Calculate the restrictions ||\begin{align}4x-5&\neq0\\4x&\neq5\\x&\neq\dfrac{5}{4}\end{align}||
-
Perform cross-multiplication||\begin{align}\dfrac{\color{#FA7921}{-2x}}{\color{#3A9A38}{4x-5}}&=\color{#3A9A38}2\\\color{#FA7921}{-2x}&=\color{#3A9A38}2(\color{#3A9A38}{4x-5})\end{align}||
-
Solve the equation||\begin{align}-2x&=8x-10\\-10x&=-10\\x&=1\end{align}||
-
Verify the solution of the equation
Since |1\neq \dfrac{5}{4},| the solution is valid. -
Determine the solution set of the inequality
Now, draw the graph of the rational function.
The vertical asymptote |x=\dfrac{5}{4}| corresponds to the restriction determined in step 3.
First, draw the function |f(x)=\dfrac{-2x}{4x-5}-3,| then draw a horizontal line at |\color{#333FB1}{y=-1}.| This gives the point of intersection |(\color{#3B87CD}{1},-1)| whose |\color{#3B87CD}x|-coordinate corresponds to the solution determined in step 5.
We are looking for the values of |x| for which |f(x)<-1| , so, those that are less than |-1.| These values are shown in green on the following graph.
By analyzing the graph, we deduce that the solution set corresponds to the values of |x| less than |1| and greater than |\dfrac{5}{4}| (the vertical asymptote).
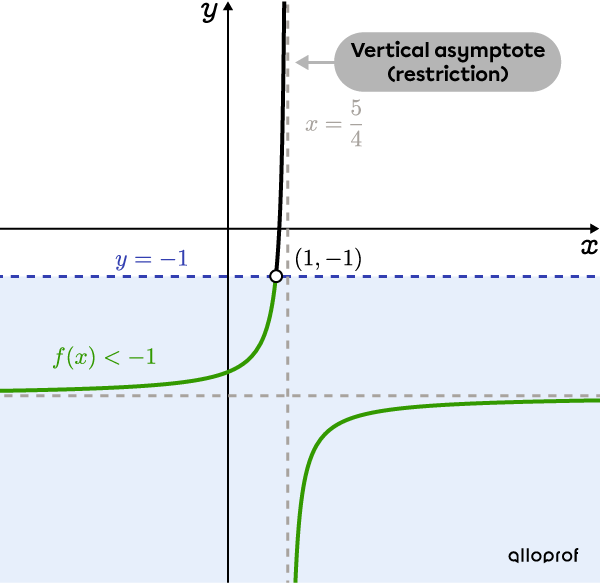
Answer: The solution set is |x\in\left]-\infty,1\right[\cup\left]\dfrac{5}{4},\infty\right[.|
Note: Since |x\neq \dfrac{5}{4}|, it must be excluded from the answer using an open square bracket. |1| is excluded, because the inequality sign is |<| and not |\leq.|