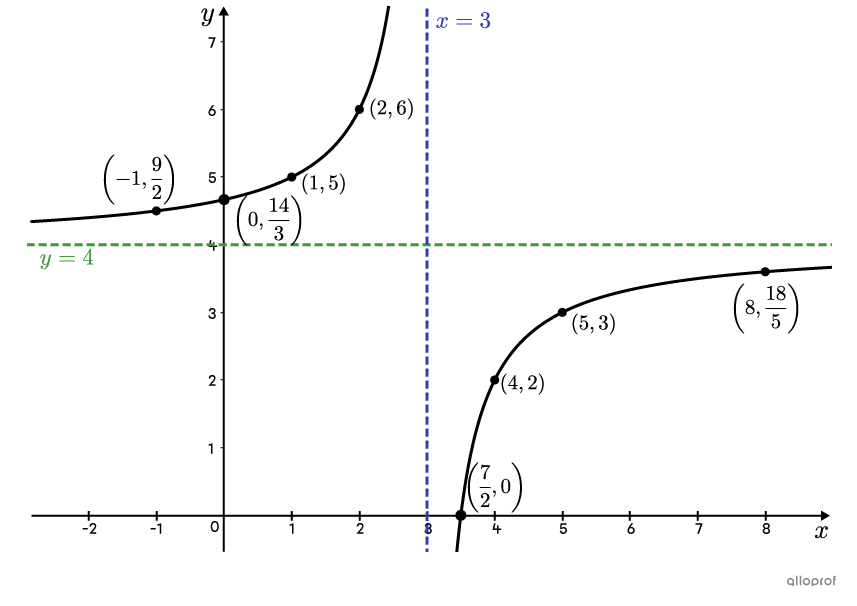To sketch the graph of a rational function, make sure the function’s rule is written in standard form.
The rational function’s rule in standard form is |f(x)=\dfrac{a}{b(x-h)}+k.|
The graph can quickly be sketched by observing parameters |a,| |b,| |h,| and |k.|
-
The rational function’s graph includes 2 asymptotes:
- a vertical asymptote at |x=h;|
- a horizontal asymptote at |y=k.| -
The location of the function’s 2 branches is decided by the sign of parameters |a| and |b.|
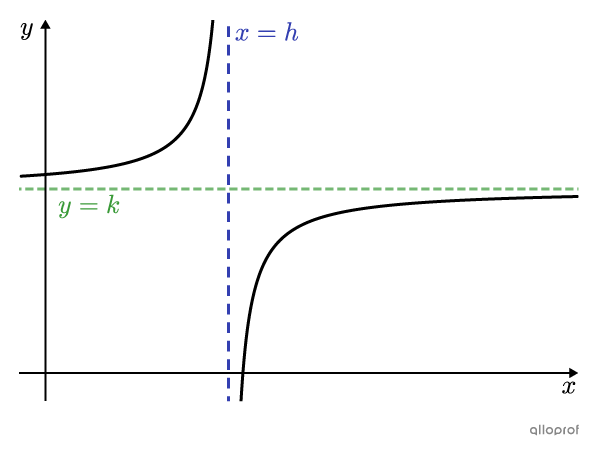
When |a| and |b| have the same sign |(ab>0),| the 2 curves are decreasing. They are located at the top right and bottom left of the asymptotes.
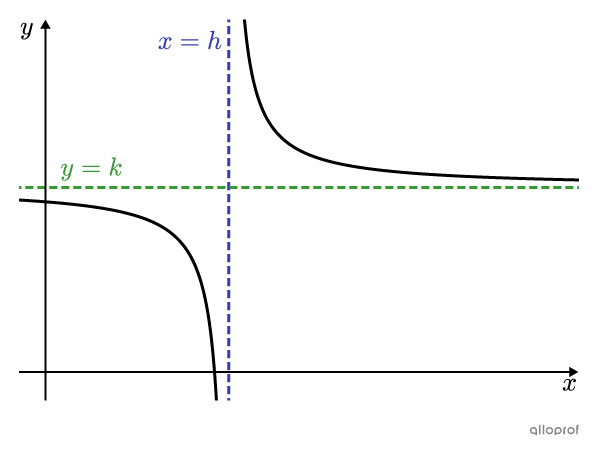
When |a| and |b| have opposite signs |(ab<0),| the 2 curves are increasing. They are located at the top left and bottom right of the asymptotes.
Note: A rational function’s curve, formed by 2 branches, is a hyperbola.
Use the following procedure to accurately sketch the graph of a rational function.
-
Find the asymptotes’ equations using parameters |h| and |k.|
-
Find the coordinates of some points.
-
Draw the 2 asymptotes and plot the points found on the Cartesian plane.
-
Sketch the 2 curves through the points located previously that approach the asymptotes without touching them.
Although they don't always exist for a rational function, the |y|-intercept and zero of the function are two useful points when sketching a graph.
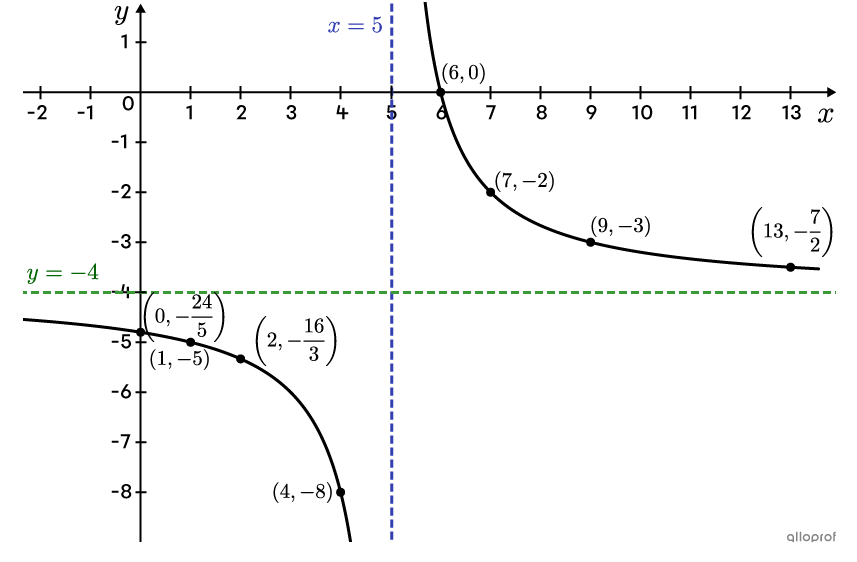
Graph the following rational function.
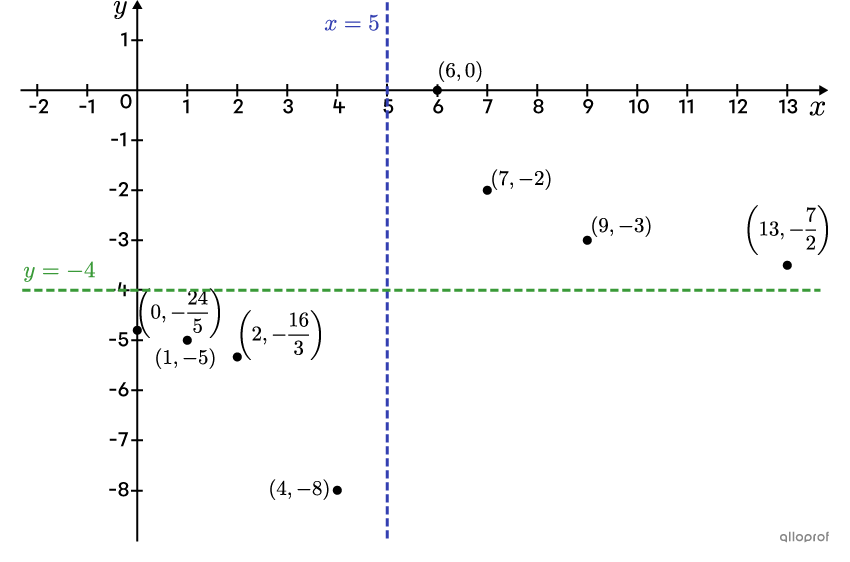
||f(x)=\dfrac{8}{2(x-5)}-4||
-
Find the asymptotes’ equations using parameters |h| and |k|
The vertical asymptote’s equation is given by |\color{#3b87cd}{x=h},| so |\color{#3b87cd}{x=5}.|
The horizontal asymptote’s equation is given by |\color{#3a9a38}{y=k},| so |\color{#3a9a38}{y=-4}.| -
Find the coordinates of some points
|
Replace |x| with |0.| |
Then, replace |x| with |1.| |
|---|---|
|
||\begin{align} This gives the point |\left(0,-\dfrac{24}{5}\right).| |
||\begin{align} |
With this approach, it’s possible to find other points.
||\left(2,-\dfrac{16}{3}\right),| |(4,-8),| |(7,-2),| |(9,-3),| |\left(13,-\dfrac{7}{2}\right)||
To find the zero of the function as well, replace |f(x)| with |0| and isolate |x.|
||\begin{align} \color{#560fa5}{f(x)}&=\dfrac{8}{2(x-5)}-4 \\
\color{#560fa5}{0}&=\dfrac{8}{2(x-5)}-4\\
\color{#ff55c3}{4}&=\dfrac{8}{\color{#ff55c3}{2(x-5)}} \\
\color{#ff55c3}{2(x-5)}&=\dfrac{8}{\color{#ff55c3}{4}} \\
2(x-5)&=2 \\x-5 &= 1\\x &=6 \end{align}||
This gives the point |(6,0).|
-
Draw the 2 asymptotes and locate the points found on the Cartesian plane
-
Sketch the graph of the 2 curves through the points located previously that approach the asymptotes without touching them
Graph the following rational function.
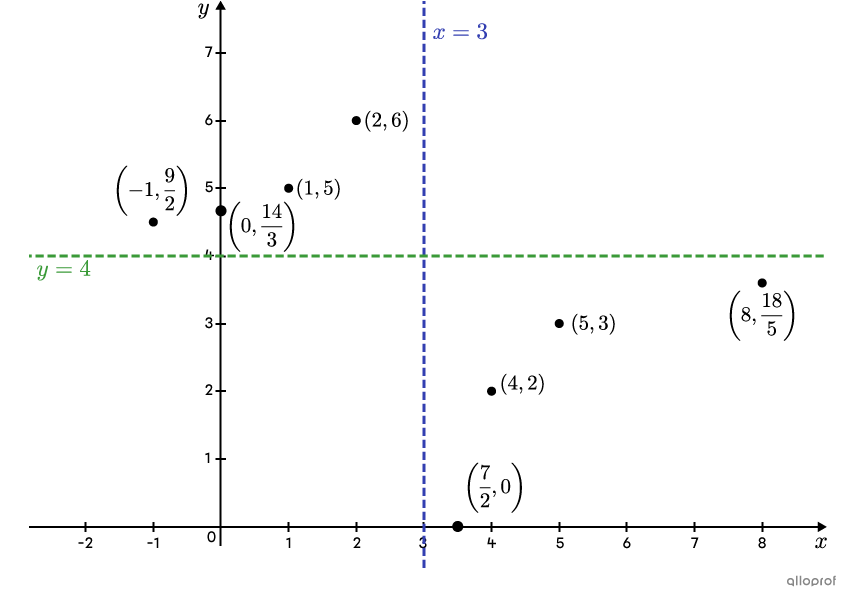
||f(x) = \dfrac{4x-14}{x-3}||
-
Find the asymptotes’ equations using parameters |h| and |k|
To determine the value of parameters |h| and |k,| convert the rule into standard form by completing a division.
||\begin{align}
\color{#3a9a38}{+4}\phantom{)} \\
\color{#3b87cd}{x-3}{\overline{\smash{\big)}\,4x-14\phantom{)}}}\\
\underline{-~\phantom{(}(4x-12){}}\\
\color{#ec0000}{-2}\phantom{)}\\
\end{align}||
This gives the following rule.
||f(x)=\dfrac{\color{#ec0000}{-2}}{\color{#3b87cd}{x-3}}\color{#3a9a38}{+4}||
The vertical asymptote’s equation is given by |\color{#3b87cd}{x=h}|, so |\color{#3b87cd}{x=3}.|
The horizontal asymptote’s equation is given by |\color{#3a9a38}{y=k}|, so |\color{#3a9a38}{y=4}.| -
Find the coordinates of some points
Note: The rule can be used in general form or standard form to calculate the coordinates of various points on the curve.
|
Replace |x| with |-1.| |
Then, replace |x| with |0.| |
|---|---|
|
||\begin{align} This gives the point |\left(-1,\dfrac{9}{2}\right).| |
||\begin{align} f(x) &= \dfrac{4x-14}{x-3}\\ f(0) &= \dfrac{4(0)-14}{(0)-3}\\ &= \dfrac{-14}{-3}\\ &=\dfrac{14}{3}\end{align}|| This gives the point |\left(0,\dfrac{14}{3}\right).| |
With this approach, other points can be found.
|(1,5),| |(2,6),| |(4,2),| |(5,3),| |\left(8,\dfrac{18}{5}\right)|
To find the zero of the function as well, replace |f(x)| with |0| and isolate |x.|
||\begin{align} f(x) &= \dfrac{4x-14}{x-3}\\ 0 &= \dfrac{4x-14}{x-3}\\ 0 &= 4x-14\\ 14 &= 4x \\ \dfrac{7}{2} &= x\end{align}||
This gives the point |\left(\dfrac{7}{2},0\right).|
-
Draw the 2 asymptotes and locate the points found on the Cartesian plane
-
Sketch the 2 curves through the points located previously that approach the asymptotes without touching them