Résoudre une équation ou une inéquation rationnelle

Une équation ou une inéquation rationnelle contient une variable qui apparait au moins une fois au dénominateur.

Puisqu'il est impossible de diviser par |0,| il faut poser des restrictions sur la variable afin que le dénominateur de la fraction rationnelle soit différent de |0.|

Ces restrictions doivent être posées avant de résoudre l'équation rationnelle.

1. Isoler la fraction.

2. Calculer les restrictions.

3. Effectuer un produit croisé.

4. Résoudre l’équation.

5. Valider la ou les solution(s).

6. Donner la ou les solution(s).

La technique du produit croisé, aussi appelée la technique du produit des extrêmes et des moyens, est une stratégie rapide et efficace lorsqu’on résout des équations rationnelles. Par contre, on peut aussi utiliser les opérations inverses et obtenir le même résultat.

Résous l'équation |\dfrac{2}{x-2}+1=5.|

1. Isoler la fraction||\begin{align}\dfrac{2}{x-2}+1&=5\\\dfrac{2}{x-2}&=4\end{align}||

2. Calculer les restrictions ||\begin{align}x-2&\neq0\\x&\neq2\end{align}||

3. Effectuer un produit croisé ||\begin{align}\dfrac{\color{#FA7921}2}{\color{#3A9A38}{x-2}}&=\color{#3A9A38}4\\\color{#FA7921}2&=\color{#3A9A38}4(\color{#3A9A38}{x-2})\end{align}||

4. Résoudre l’équation ||\begin{align}2&=4x-8\\10&=4x\\2{,}5&=x\end{align}||

5. Valider la solution
   Puisque |2{,}5\neq 2,| la solution est valide.

6. Donner la solution
   La solution de l’équation |\dfrac{2}{x-2}+1=5| est |x=2{,}5.|

Il y a 2 façons de valider la solution obtenue.

1. S’assurer que la solution respecte la restriction déterminée à l’étape 2, comme le montre l’exemple précédent.

2. Substituer la solution dans l’équation de départ. Dans l’exemple précédent, on remplace la variable |x| dans l’équation de départ et on s’assure que le membre de gauche est équivalent au membre de droite.||\begin{align}\dfrac{2}{\color{#3B87CD}x-2}+1&=5\\ \dfrac{2}{\color{#3B87CD}{2{,}5}-2}+1&\stackrel{?}{=}5\\4+1&\stackrel{?}{=}5\\5&=5\end{align}||La solution est bel et bien valide.

Résous l'équation |\dfrac{3+2x}{x}=8.|

1. Isoler la fraction 
   Puisque la fraction est déjà isolée, on peut passer à la prochaine étape.

2. Calculer les restrictions ||x\neq 0||

3. Effectuer un produit croisé ||\begin{align}\dfrac{\color{#FA7921}{3+2x}}{\color{#3A9A38}x}&=\color{#3A9A38}8\\\color{#FA7921}{3+2x}&=\color{#3A9A38}8(\color{#3A9A38}x)\end{align}||

4. Résoudre l'équation ||\begin{align}3+2x&=8x\\3&=6x\\0{,}5&=x\end{align}||

5. Valider la solution
   Puisque |0{,}5\neq 0,| la solution est valide.

6. Donner la solution
   La solution de l’équation |\dfrac{3+2x}{x}=8| est |x=0{,}5.|

Résous l'équation |\dfrac{2x+5}{x-7}=2.|

1. Isoler la fraction
   Puisque la fraction est déjà isolée, on peut passer à la prochaine étape.

2. Calculer les restrictions ||\begin{align}x-7&\neq0\\x&\neq7\end{align}||

3. Effectuer un produit croisé ||\begin{align}\dfrac{\color{#FA7921}{2x+5}}{\color{#3A9A38}{x-7}}&=\color{#3A9A38}2\\\color{#FA7921}{2x+5}&=\color{#3A9A38}2(\color{#3A9A38}{x-7})\end{align}||

4. Résoudre l'équation ||\begin{align}2x+5&=2x-14\\0x&=-19\\0&=-19\end{align}|| À cette étape, on doit arrêter la résolution, car on se retrouve devant une fausse égalité : |0| n’est pas égal à |-19.| L’équation ne possède aucune solution.

5. Valider la solution
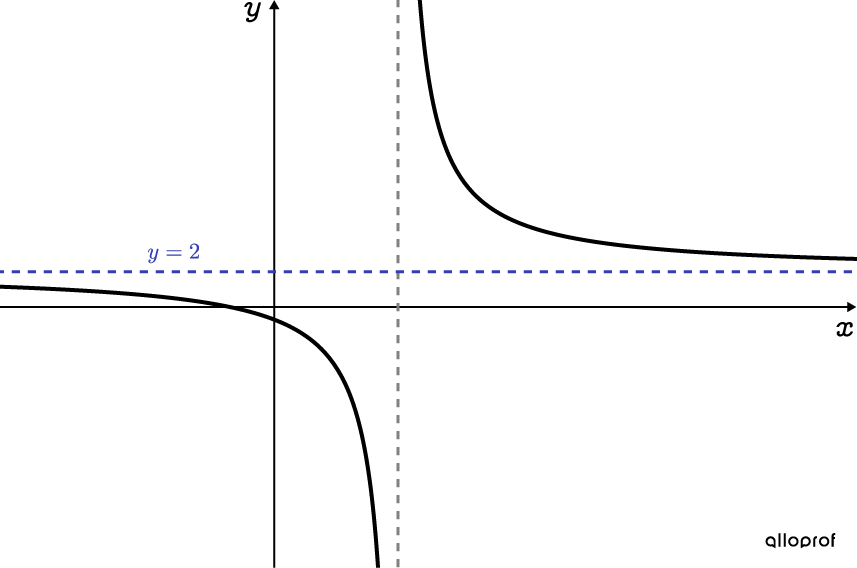
   Puisque l’équation ne possède aucune solution, cette étape est facultative. Toutefois, il est possible de valider l’absence de solution à l’aide du graphique de la fonction rationnelle.
   
   On représente la fonction |f(x)=\dfrac{2x+5}{x-7}|. On doit déterminer pour quelle(s) valeur(s) de |x| cette fonction est égale à |2,| autrement dit à |\color{#333FB1}{y=2}.| Puisque l’asymptote de la fonction est |\color{#333FB1}{y=2}|, il est impossible d’obtenir une solution (un point de rencontre) avec la fonction.

6. Donner l’ensemble-solution
   Il n’existe aucune solution pour l’équation |\dfrac{2x+5}{x-7}=2.|

Résous l'équation |\dfrac{2x+6}{x-2}=x+3.|

1. Isoler la fraction
   Puisque la fraction est déjà isolée, on peut passer à la prochaine étape.

2. Calculer les restrictions||\begin{align}x-2&\neq 0\\x&\neq 2\end{align}||

3. Effectuer un produit croisé ||\begin{align}\dfrac{\color{#FA7921}{2x+6}}{\color{#3A9A38}{x-2}}&=\color{#3A9A38}{x+3}\\\color{#FA7921}{2x+6}&=(\color{#3A9A38}{x-2})(\color{#3A9A38}{x+3})\\2x+6&=x^2+x-6\end{align}||

4. Résoudre l’équation
   À l’étape précédente, on a obtenu une équation du second degré. Pour la résoudre, on peut utiliser la formule quadratique.||\begin{align}2x+6&=x^2+x-6\\0&=x^2-x-12\end{align}||||\begin{align}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\&=\dfrac{-(-1)\pm\sqrt{(-1)^2-4(1)(-12)}}{2(1)}\\\\&=\dfrac{1\pm\sqrt{49}}{2}\\\\x&\in\{-3,4\}\end{align}||

5. Valider les solutions
   Puisque |-3\neq 2| et |4\neq 2,| les solutions sont valides.

6. Donner l’ensemble-solution
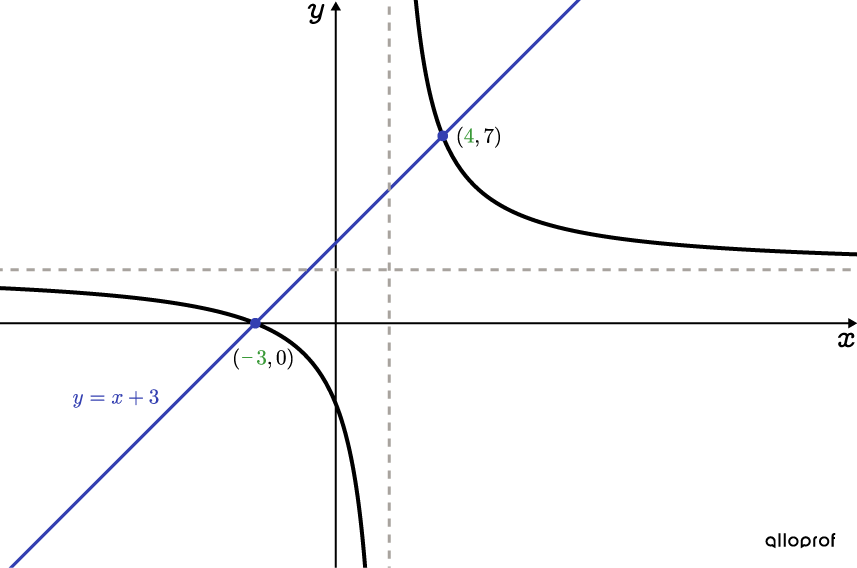
   L’ensemble-solution de l’équation |\dfrac{2x+6}{x-2}=x+3| est |x\in\left\{-3,4\right\}.|

On peut bien voir l’ensemble-solution à l’aide d’une représentation graphique. On trace la fonction |f(x)=\dfrac{2x+6}{x-2}|, puis la droite d’équation |\color{#333FB1}{y=x+3}.| Puisque la droite est oblique et non horizontale, on remarque 2 points d’intersection. La coordonnée |\color{#3A9A38}x| de ces points correspond aux solutions déterminées à l’étape 4.

1. Remplacer le symbole d’inégalité par le symbole d’égalité.

2. Isoler la fraction.

3. Calculer les restrictions.

4. Effectuer un produit croisé.

5. Résoudre l’équation.

6. Valider la solution de l’équation.

7. Déterminer l’ensemble-solution de l’inéquation à l’aide d’un graphique ou d’une droite numérique.

Résous l'inéquation |\dfrac{3}{x-1}+4\geq 6.|

1. Remplacer le symbole d’inégalité par le symbole d’égalité||\dfrac{3}{x-1}+4=6||

2. Isoler la fraction||\dfrac{3}{x-1}=2||

3. Calculer les restrictions||\begin{align}x-1&\neq 0\\x&\neq1\end{align}||

4. Effectuer un produit croisé||\begin{align}\dfrac{\color{#FA7921}3}{\color{#3A9A38}{x-1}}&=\color{#3A9A38}2\\\color{#FA7921}3&=\color{#3A9A38}2(\color{#3A9A38}{x-1})\end{align}||

5. Résoudre l'équation||\begin{align}3&=2x-2\\5&=2x\\2{,}5&=x\end{align}||

6. Valider la solution de l’équation
   Puisque |2{,}5\neq 1,| la solution est valide.

7. Déterminer l’ensemble-solution de l’inéquation
   Pour déterminer l’ensemble-solution, on peut tracer le graphique de la fonction rationnelle.

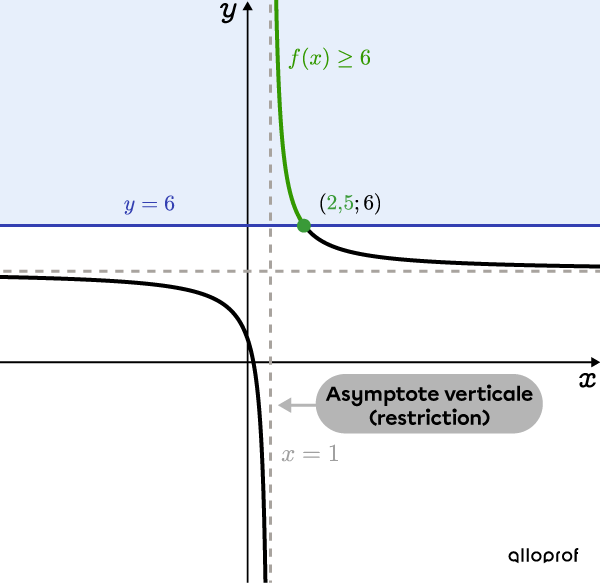
Réponse : L’ensemble-solution est |x\in \left]1;2{,}5\right].|

Remarque : Puisque |x\neq 1|, on doit l’exclure de la réponse en utilisant un crochet ouvert. |2{,}5| est inclus, puisque le signe d’inéquation est |\geq| et non |>.|

Pour déterminer l’ensemble-solution (étape 7), il est possible de ne pas utiliser de représentation graphique, mais plutôt une droite numérique. En utilisant l’exemple précédent, voici comment procéder.

Ces 2 valeurs de |x| séparent la droite numérique en 3 intervalles : |]-\infty, 1[,| |]1; 2{,}5]| et |[2{,}5,+\infty[.| Il faut donc valider une valeur au hasard dans chacune de ces sections dans l’inéquation de départ.

• Pour |]-\infty, 1[,| on utilise |x=0.|||\begin{align}\dfrac{3}{\color{#3B87CD}x-1}+4&\geq6\\ \dfrac{3}{\color{#3B87CD}{0}-1}+4&\stackrel{?}{\geq}6\\1&\color{#ec0000}{\not\geq}6\ \end{align}||On obtient |1\color{#EC0000}{\not\geq} 6.| On en conclut que toutes les valeurs inférieures à |1| ne peuvent pas correspondre à l’ensemble-solution.

• Pour |]1;2{,}5]|, on utilise |x=2.|
  On obtient |7\geq 6.| Comme c’est vrai, on en conclut que l’intervalle |]1;2{,}5]| fait partie de l’ensemble-solution.

• Pour |[2{,}5;+\infty[,| on utilise |x=4.|
  On obtient |5\color{red}{\not \geq} 6.| On en conclut que toutes les valeurs supérieures à |2{,}5| ne peuvent pas correspondre à l’ensemble-solution.

Résous l'inéquation |\dfrac{-2x}{4x-5}-3<-1.|

1. Remplacer le symbole d’inégalité par le symbole d’égalité||\dfrac{-2x}{4x-5}-3=-1||

2. Isoler la fraction||\dfrac{-2x}{4x-5}=2||

3. Calculer les restrictions||\begin{align}4x-5&\neq0\\4x&\neq5\\x&\neq\dfrac{5}{4}\end{align}||

4. Effectuer un produit croisé||\begin{align}\dfrac{\color{#FA7921}{-2x}}{\color{#3A9A38}{4x-5}}&=\color{#3A9A38}2\\\color{#FA7921}{-2x}&=\color{#3A9A38}2(\color{#3A9A38}{4x-5})\end{align}||

5. Résoudre l'équation||\begin{align}-2x&=8x-10\\-10x&=-10\\x&=1\end{align}||

6. Valider la solution de l’équation
   Puisque |1\neq \dfrac{5}{4},| la solution est valide.

7. Déterminer l’ensemble-solution de l’inéquation
   On trace le graphique de la fonction rationnelle.

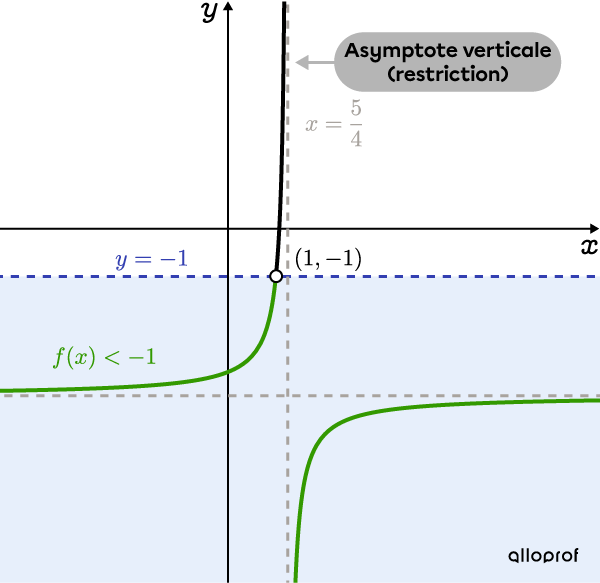
Réponse : L’ensemble-solution est |x\in\left]-\infty,1\right[\cup\left]\dfrac{5}{4},\infty\right[.|

Remarque : Puisque |x\neq \dfrac{5}{4}|, on doit l’exclure de la réponse en utilisant un crochet ouvert. |1| est exclu, puisque le signe d’inéquation est |<| et non |\leq.|