Given the particular properties of a cube, several pairs of congruent sides can form its bases. The bases of a cube are always two congruent squares. Thus, we can use the following formula.
||A_\text{b} = s^2|| where ||\begin{align}A_b&= \text{Area of a base}\\s &= \text{side}\end{align}||
Note: if the area of the bases is needed, you must multiply the area of one base by |2| since there are two congruent bases.
Calculate the area of the bases of the following cube.
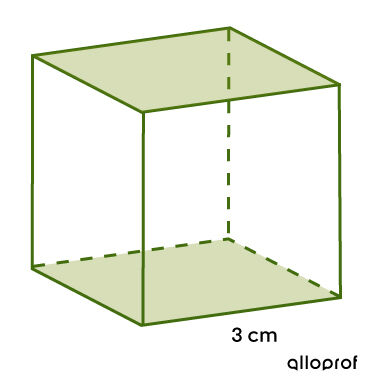
-
Identify the relevant faces
In this case, they are already identified. -
Apply the formula
It is a cube, so the following formula can be applied. ||\begin{align}A_\text{b} &= \color{#3a9438}{s}^2 \\ &= \color{#3a9438}{3}^2\\ &= 9\ \text{cm}^2\end{align}||Since we are looking for the area of the bases, multiply the area of one base by 2. ||\begin{align}A_\text{bases} &= 2\times 9 \\ &= 18\ \text{cm}^2\end{align}|| -
Interpret the answer
Therefore, the cube’s bases have a total area of |18 \ \text{cm}^2.|
Due to the particular construction of a cube, the same reasoning can be applied for the lateral area.
Since the four lateral faces are congruent squares, simply calculate the area of one face and multiply it by |4| to obtain the lateral area.
||A_L = 4 s^2|| where ||\begin{align} A_L &= \text{Lateral area of a cube}\\s &= \text{side}\end{align}||
We want to paint the four walls of a cube-shaped room the same colour. Knowing that one can of paint covers |32\ \text{m}^2,| determine the number of cans needed to complete the job.
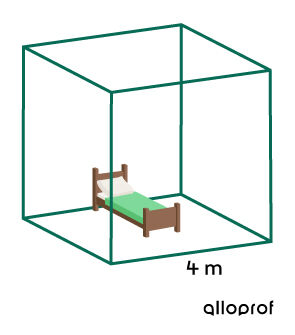
-
Identify the relevant faces
There are four walls which form the lateral area and need to be painted.
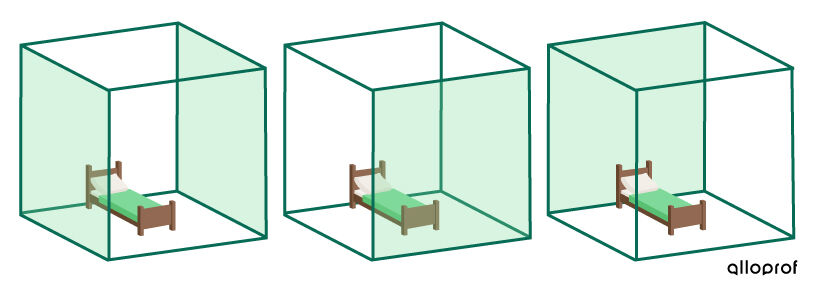
-
Apply the formula
||\begin{align}A_L &= 4 c^2 \\ &= 4 (4)^2 \\ &= 64 \ \text{m}^2\end{align}|| -
Interpret the answer
Since it is necessary to cover an area of |64 \ \text{m}^2| and one can of paint covers |32 \ \text{m}^2,| simply divide as follows. ||64\ \text{m}^2 \div \dfrac{32\ \text{m}^2}{1\ \text{can}} = 2\ \text{cans}|| To paint the four walls, |2| cans of paint will be needed.
Once again, use the fact that a cube’s faces are composed of six congruent squares to derive its area formula.
||A_T = 6 s^2|| where ||\begin{align}A_T&= \text{Total area of a cube}\\s &= \text{side}\end{align}||
In fact, it is simply a matter of calculating the area of one of the faces and multiplying it by |6| since they are congruent.
Note: since a cube is also a prism, the following formula can equally be used: |A_T=2A_b+A_L.|
A company is tasked with polishing and restoring the lustre of dice used in their casinos. If polishing costs |$0{.}25\ / \text{cm}^2,| how much will it cost to polish 200 dice?
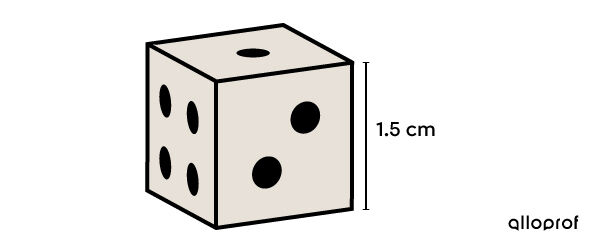
-
Identify the relevant faces
In this case, the six faces must be polished. -
Apply the formula
||\begin{align} A_T &= 6 c^2 \\ &= 6 (1{.}5)^2 \\ &= 13{.}5 \ \text{cm}^2\end{align}|| -
Interpret the answer
If there are |200| dice, the total surface area is ||\dfrac {13{.}5\ \text{cm}^2}{1\ \text{die}} \times 200\ \text{dice} = 2\ 700\ \text{cm}^2|| Since it costs |$0{.}25\ / \text{cm}^2| : ||2\ 700\ \text{cm}^2 \times $0{.}25\ / \text{cm}^2 = $675\ || It will cost |$675\ | to polish all the dice of the casinos.
In some cases, a missing side measurement may be sought from a given area. This is called finding a missing measurement of a cube from its area. In this context, the approach is a little different, but it is still essential to remember the formula for finding the surface area of a cube.