Pour calculer l’aire du cube, il est important de se rappeler que le cube est un cas particulier des prismes et qu’il répond aux mêmes formules d’aire que ces derniers. Toutefois, il existe des formules plus simples pour le cube.
Il est possible de déduire les formules d'aire du cube en analysant son développement.
Étant donné les propriétés particulières du cube, plusieurs paires de côtés isométriques peuvent former ses bases. Les bases du cube sont obligatoirement 2 carrés isométriques. Ainsi, on peut utiliser la formule suivante :
||A_\text{b} = c^2||où||\begin{align}A_b&: \text{Aire d’une base}\\c &: \text{côté}\end{align}||
Remarque : Si on cherche à déterminer l’aire des bases, il faudra multiplier l’aire d’une base par 2, car on a 2 bases isométriques.
Calcule l'aire des bases du cube suivant :
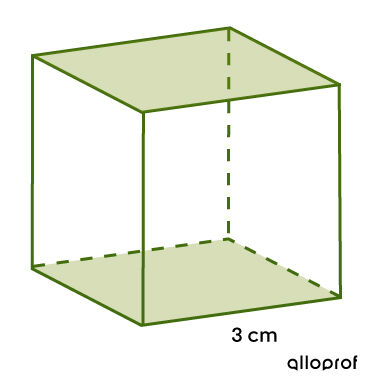
-
Identifier les faces concernées
Dans le cas présent, elles sont déjà identifiées. -
Appliquer la formule
Puisqu'il s'agit d'un cube, on peut appliquer la formule||\begin{align}A_\text{b} &= \color{#3a9438}{c}^2 \\ &= \color{#3a9438}{3}^2\\ &= 9\ \text{cm}^2\end{align}||Comme on cherche l’aire des bases, il suffit de multiplier l’aire d’une base par 2.||\begin{align}A_\text{bases} &= 2\times 9 \\ &= 18\ \text{cm}^2\end{align}|| -
Interpréter la réponse
L'aire des bases du cube est donc de |18 \ \text{cm}^2.|
Étant donné la construction particulière du cube, on peut appliquer le même raisonnement pour l'aire latérale.
Puisque les 4 faces latérales sont des carrés isométriques, il suffit de calculer l'aire de l’une d'entre elles et de la multiplier par 4 pour obtenir l’aire latérale.
||A_L = 4 c^2||où||\begin{align} A_L &: \text{Aire latérale du cube}\\c &: \text{côté}\end{align}||
Dans une chambre de forme cubique, on veut peinturer les 4 murs de la même couleur. En sachant qu'un pot de peinture couvre |32\ \text{m}^2,| détermine le nombre de pots qu'il faudra acheter pour accomplir la tâche.
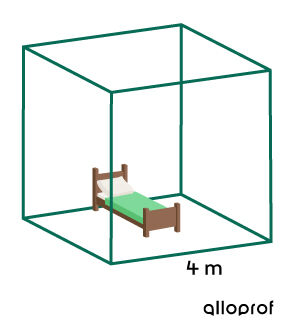
-
Identifier les faces concernées
Dans le cas présent, il y a un total de 4 murs à peinturer qui forment l’aire latérale.
-
Appliquer la formule
||\begin{align}A_L &= 4 c^2 \\ &= 4 (4)^2 \\ &= 64 \ \text{m}^2\end{align}|| -
Interpréter la réponse
Puisqu'il faut couvrir une surface de |64 \ \text{m}^2| et qu'un pot couvre |32 \ \text{m}^2,| il suffit d'effectuer la division suivante : ||64\ \text{m}^2 \div \dfrac{32\ \text{m}^2}{1\ \text{pot}} = 2\ \text{pots}||Pour peinturer les |4| murs, |2| pots de peinture seront nécessaires.
Une fois de plus, on peut utiliser le fait que les faces du cube sont composées de 6 carrés isométriques pour déduire la formule associée à son aire totale.
||A_T = 6 c^2||où||\begin{align}A_T&: \text{Aire totale du cube}\\c &: \text{côté}\end{align}||
Dans les faits, il s'agit de calculer l'aire d'une des faces et de la multiplier par 6 étant donné qu'elles sont isométriques.
Remarque : Comme le cube est aussi un prisme, on peut également utiliser la formule |A_T=2A_b+A_L.|
Une compagnie s'affaire à polir et rendre le lustre initial aux dés utilisés dans les casinos. Si le polissage coute |0{,}25\ $ / \text{cm}^2,| à combien s'élèvera la facture si les 200 dés qu'on doit faire polir ont cette allure?
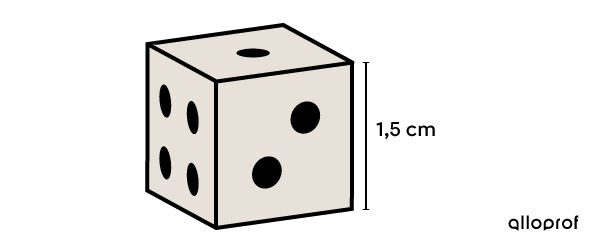
-
Identifier les faces concernées
Dans le cas présent, ce sont les 6 faces qui doivent être polies. -
Appliquer la formule
||\begin{align} A_T &= 6 c^2 \\ &= 6 (1{,}5)^2 \\ &= 13{,}5 \ \text{cm}^2\end{align}|| -
Interpréter la réponse
Si on a |200| dés, on obtient une surface totale de ||\dfrac {13{,}5\ \text{cm}^2}{1\ \text{dé}} \times 200\ \text{dés} = 2\ 700\ \text{cm}^2||Comme il en coute |0{,}25\ $ / \text{cm}^2| :||2\ 700\ \text{cm}^2 \times 0{,}25\ $ / \text{cm}^2 = 675\ $||Il en coutera finalement |675\ $| pour polir tous les dés du casino.
Dans d'autres circonstances, on pourrait s'intéresser à la mesure du côté alors que l’aire totale est donnée. C’est ce qui s’appelle trouver une mesure manquante d'un cube à partir de l'aire. Dans ce cas, la démarche est un peu différente, mais il demeure essentiel de se rappeler la formule de l’aire totale associée au cube.