It is important to recognize the different parts of a pyramid to identify it. In other words, we must recognize the figures that form its base, the lateral faces, and its height. The area can be calculated once this step is complete.
Since a pyramid can have any polygon as its base, it is essential to identify it accurately when calculating the area. Refer to the formulas for calculating the area of plane figures to understand which one to use based on the type of polygon that forms the base. The area of the base is denoted as |A_b.|
What is the area of the base of the following regular pyramid?
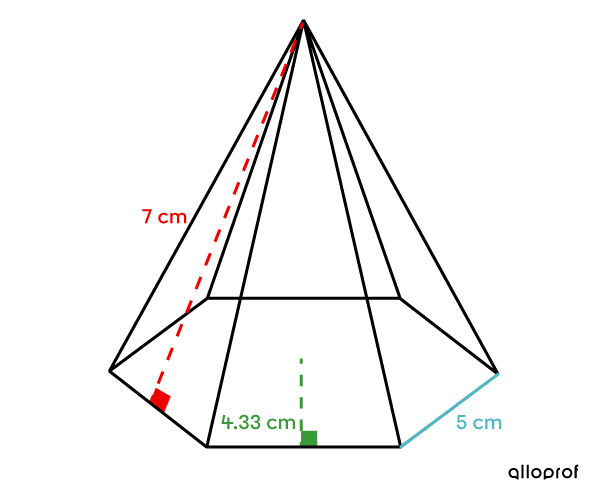
-
Identify the relevant shapes
The base is a regular hexagon. -
Apply the appropriate formula
Since this plane figure is a regular polygon, apply this formula: ||\begin{align} A_b &=A_{\text{regular polygons}}\\\\&= \dfrac{\color{#51B6C2}{s} \times \color{#3A9A38}{a_b} \times n}{2}\\\\&= \dfrac{\color{#51B6C2}{5} \times \color{#3A9A38}{4{.}33} \times 6}{2}\\\\&= 64{.}95 \ \text{cm}^2 \end{align}|| -
Interpret the answer
Since there is no context involved in this problem, simply state that the pyramid’s base area is |64.95\ \text{cm}^2.|
Since a regular pyramid is, in fact, a pyramid with a regular polygon as its base, be careful not to confuse the base’s apothem with that of the pyramid.
The apothem is usually identified by the variable |a.| To differentiate between the two apothems, add a subscript. Thus, the pyramid’s apothem becomes |a_p| and the base’s apothem becomes |a_b.| The choice of the subscript or the way of identifying the 2 measures may vary in different contexts.
To calculate a pyramid’s lateral area, it is important to know whether it is a regular pyramid or not.
The lateral area of a regular pyramid
When the solid is a right pyramid whose base is a regular polygon, the lateral faces are congruent isosceles triangles.
||A_L = \dfrac{P_b \times a_p}{2}|| where ||\begin{align}A_L&=\text{Lateral area}\\P_b&=\text{Base perimeter}\\a_p &= \text{Pyramid apothem}\end{align}||
The facades of some of Egypt's pyramids need to be restored in order to keep them open to the public. The surface area of the square pyramid of Khephren needs to be found before companies can be sent a call for tender.
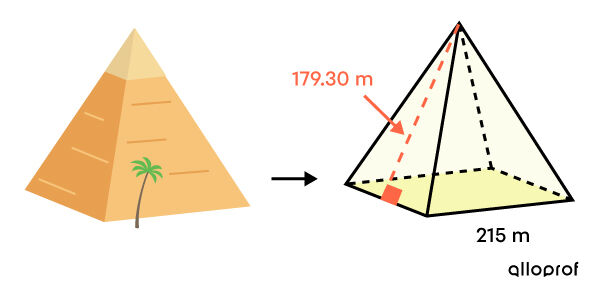
-
Identify the solid
It is a square-based pyramid. Therefore, we are looking for the lateral area of a regular pyramid. -
Apply the lateral area formula of the identified solid
||\begin{align} A_L &=\dfrac{P_b \times \color{#FA7921}{a_p}}{2}\\\\&=\dfrac{(215+215+215+215) \times \color{#FA7921}{179{.}30}}{2}\\\\&= 77\ 099 \ \text{m}^2\end{align}|| -
Interpret the answer
The surface area to be restored is equivalent to |77\ 099\ \text{m}^2.|
Note: Because it is a square-based pyramid, the same answer can be obtained by calculating the area of a single lateral face (a triangle) and multiplying it by 4.
Here are some additional explanations to help explain the formula.
Demonstrating the formula for the lateral area of a regular pyramid
-
Construct the net of the pyramid.
The base of each triangle can be associated with one side of the pyramid’s base.
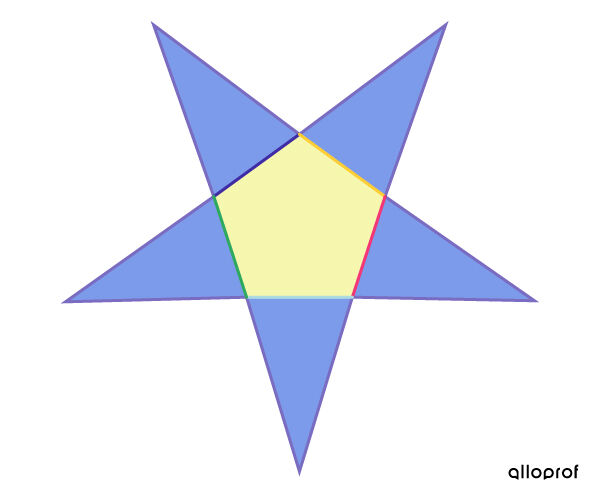
-
Place the triangles side by side.
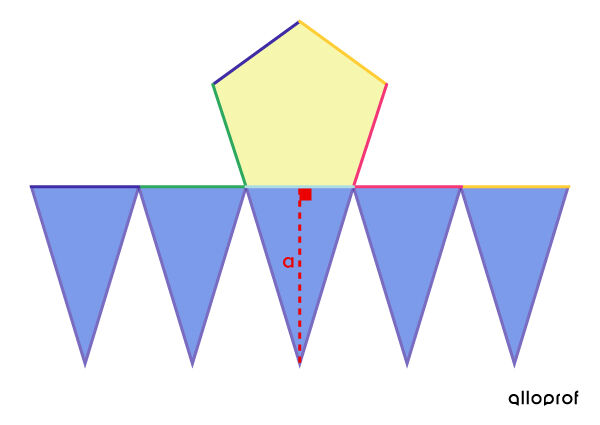
-
Drag the vertices of each triangle so they meet at the same point.
Although the triangles have changed, the area of each of the five triangles remains the same since their bases and heights maintain their measurements. Therefore, the lateral area of the pyramid is always the same.
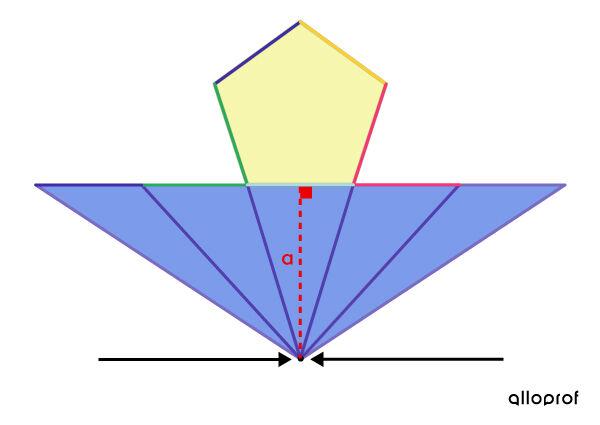
-
The 5 triangles now form only 1 triangle. The triangle’s area is calculated with the new base and the height of one of the triangles forming the lateral area.

Therefore, the usual formula for the area of a triangle is used: |A = \dfrac{b\times h}{2}.| Since the large triangle’s base corresponds to the base’s perimeter, replace |b| with |P_b|, and since the triangle’s height corresponds to the pyramid’s apothem, replace |h| with |a.| Thus, we obtain the formula for the lateral area of the above regular pyramid. ||\begin{align} \color{#333FB1}{A_L} &= \text{Area of the large triangle} \\ &= \dfrac{\color{#FA7921}b \times \color{#EC0000}{h}}{2} \\ &= \dfrac{\color{#FA7921}{P_b}\times \color{#EC0000}{a}}{2} \end{align}||
The lateral area of an irregular pyramid
There is no formula for the lateral area of an irregular pyramid. However, the lateral area can be calculated by decomposing the lateral faces into triangles. Then, calculate the area of each of the triangles separately and add them all together.
Calculate the lateral area of the following rectangular pyramid.
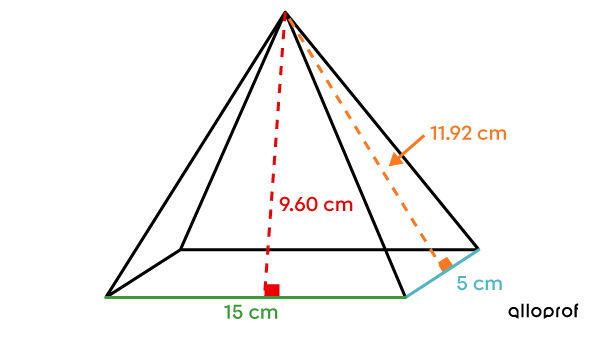
-
Identify the solid
It is a rectangular-based pyramid, so we cannot use the formula for the lateral area of a regular pyramid. The four lateral faces must be calculated separately. ||\begin{align} A_{\triangle\ \text{front}} &= A_{\triangle\ \text{back}}= \dfrac{\color{#3A9A38}{b_1}\times \color{#EC0000}{h_1}}{2} \\\\ A_{\triangle\ \text{right side}} &= A_{\triangle\ \text{left side}}= \dfrac{\color{#51b6c2}{b_2}\times \color{#FA7921}{h_2}}{2} \\\\ A_L &= 2\times A_{\triangle\ \text{front}} + 2 \times A_{\triangle\ \text{the right}}\end{align}|| -
Apply the lateral area formula of the identified solid
||\begin{align} A_{\triangle\ \text{front}} &= \dfrac{\color{#3A9A38}{15}\times \color{#EC0000}{{9{.}60}}}{2} \\ &= 72\ \text{cm}^2 \\\\ A_{\triangle\ \text{right side}} &= \dfrac{\color{#51b6c2}{5}\times \color{#FA7921}{11{.}92}}{2} \\ &=29{.}8\ \text{cm}^2 \\\\ A_L &= 2\times A_{\triangle\ \text{front}} + 2 \times A_{\triangle\ \text{the right}} \\ &= 2 \times 72 + 2 \times 29{.}8 \\ &= 203{.}6\ \text{cm}^2 \end{align}|| -
Interpret the answer
The lateral area of the pyramid is |203{.}6\ \text{cm}^2.|
The total area of a pyramid is obtained by adding its lateral and base area.
||A_T = A_L + A_b|| where ||A_T=\text{Total area}||
It is a combination of the two formulas above.
We want to cover the dice used to play Dungeons & Dragons with a particular material. Each die is in the shape of a regular tetrahedron.
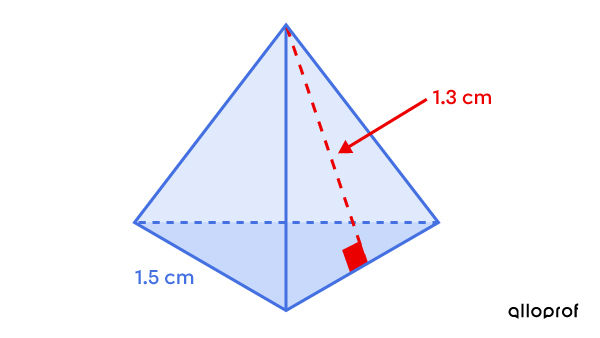
How much material will be needed if we want to cover 150 dice?
-
Identify the faces concerned
Since the dice are to be completely covered, the area of the 4 faces must be calculated (i.e., the total area). -
Calculate the base area
Since each die is a regular tetrahedron, all the faces are congruent equilateral triangles. Thus, ||\begin{align} A_b &= \dfrac{\color{#3B87CD}b \times \color{#EC0000}h}{2} \\ &= \dfrac{\color{#3B87CD}{1{.}5} \times \color{#EC0000}{1{.}3}}{2} \\ &= 0{.}975 \ \text{cm}^2\end{align}|| -
Calculate the lateral area
A tetrahedron is part of the group of regular pyramids, so: ||\begin{align} A_L &= \dfrac{\color{#3b87cd}{P_b} \times \color{#ec0000}a}{2} \\ &= \dfrac{(\color{#3b87cd}{1{.}5} + \color{#3b87cd}{1{.}5} + \color{#3b87cd}{1{.}5}) \times \color{#ec0000}{1{.}3}}{2}\\ &= 2{.}925 \ \text{cm}^2\end{align}|| -
Calculate the total area ||\begin{align} A_T &= A_L + A_b \\ &= 2{.}925 + 0{.}975\\ &= 3{.}9 \ \text{cm}^2 \end{align}||
-
Interpret the answer
We want to cover 150 dice, so the total area is |3{.}9\ \text{cm}^2/\text{die} \times 150\ \text{dice}= 585\ \text{cm}^2.|
Note: Since a regular tetrahedron is a particular solid composed of 4 equilateral triangles, its area can be calculated using the following formula.
||A_T=4\times\dfrac{b\times h}{2}|| where ||\begin{align} b &= \text{Triangle’s edge or base} \\ h &= \text{Apothem or triangle’s height} \\ A_T &= \text{Tetrahedron’s total area} \end{align}||
Sometimes, a particular base dimension or a pyramid’s apothem measurement needs to be found from a given area. This is called finding a missing measurement of a pyramid from the area. In this case, the approach is a little different, but it is still important to remember the formula for the total area of pyramids.
While there is no specific formula for calculating the measurement of a pyramid’s apothem, the Pythagorean Theorem is generally used.
Finding the measurement of the apothem from the height
In the case of a right pyramid, a right triangle can be obtained by tracing the pyramid’s apothem, the pyramid’s height, and the line segment connecting the centre of the base and the midpoint of the base’s side.
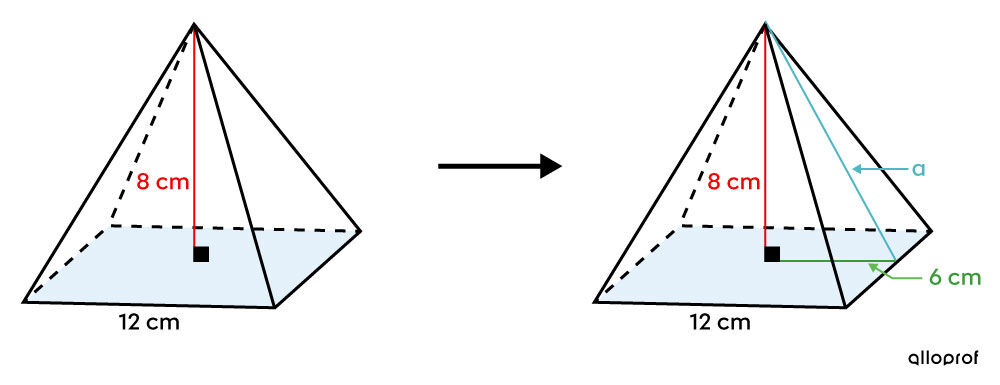
Since it is a right pyramid, and the height is located at the base’s centre, the measurement of the leg is half the measurement of the base’s side.
By associating the measurement of one leg of the right triangle with half of one side of the base and associating the other leg with the pyramid’s height, the apothem becomes the hypotenuse. Now there is enough information to use the Pythagorean Theorem: ||\begin{align} \color{#3A9A38}{a}^2 + \color{#EC0000}{b}^2 &= \color{#51B6C2}{c}^2\\\\ \color{#3A9A38}{6}^2 + \color{#EC0000}{8}^2 &= \color{#51B6C2}{a}^2\\ 100 &= \color{#51B6C2}{a}^2\\ 10\ \text{cm} &= \color{#51B6C2}{a} \end{align}||
Thus, the pyramid’s apothem is |10\ \text{cm}.|
When using several concepts simultaneously, be careful with the variables you are using. On a pyramid, |\boldsymbol{\color{#51B6C2}{a}}| refers to the apothem, while in the Pythagorean theorem, the variable |\boldsymbol{\color{#51B6C2}{c}}| refers to this same segment. To fully understand the two examples, use colours to associate the numbers with the segments they represent.
The Pythagorean Theorem is once again used to determine the measurement of a height from the apothem.
| Area of a Base ↑ | |
|---|---|
|
If the base is a triangle: |A_b=\dfrac{{b}\times{h}}{2}| |
||\begin{align}A_b&: \text{Area of a base}\\b&: \text{base of the triangle}\\h&: \text{height of the triangle}\end{align}|| |
|
If the base is a square: |\begin{align} |
||\begin{align}A_b&: \text{Area of a base}\\s&: \text{side}\end{align}|| |
|
If the base is a rectangle: |A_b={b}\times{h}| |
||\begin{align}A_b&: \text{Area of a base}\\b&: \text{base of the rectangle}\\h&: \text{height of the rectangle}\end{align}|| |
|
If the base is a regular polygon: |A_b=\dfrac{san}{2}| |
||\begin{align}A_b&: \text{Area of a base}\\s&: \text{side}\\a&: \text{apothem}\\n&: \text{number of sides}\end{align}|| |
| Lateral Area ↑ | |
|---|---|
| ||A_L = \dfrac{P_b \times a_p}{2}|| | ||\begin{align}A_L&=\text{Lateral area}\\P_b&=\text{Base perimeter}\\a_p &= \text{Pyramid apothem}\end{align}|| |
| Total Area ↑ | |
|---|---|
| ||A_T = A_L + A_b|| | ||\begin{align}A_T&:\text{Total Area}\\A_b&:\text{Area of the base} \\ A_L&: \text{Lateral Area} \end{align}|| |