Several solids meet the definition of a prism. It is important to recognize the different parts of a prism: the figures that form its bases, its lateral faces, and its height. Once this step is completed, the area can be calculated.
The bases of the prism are plane figures. It is possible to calculate the area of the bases using the area formula associated with the corresponding plane figure. Moreover, the bases are congruent, meaning that only the area of one base, denoted by |A_b,| needs to be found. Then, we can multiply it by 2 for the area of the two bases.
Note: The choice of formula varies depending on the base’s shape. Essentially, the formula is associated with the plane figure’s base. For a list of the formulas, see the summary table of perimeter and area formulas.
To attract potential customers, a company prints a life-size image of a boxed toy on the base of its packaging. Based on the measurements of the box shown below, determine the area covered by the printed image.
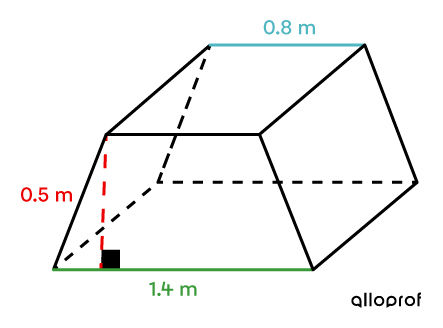
-
Identify the relevant surfaces
The bases are two trapezoids since they are the only two figures in this solid that are both parallel and congruent.
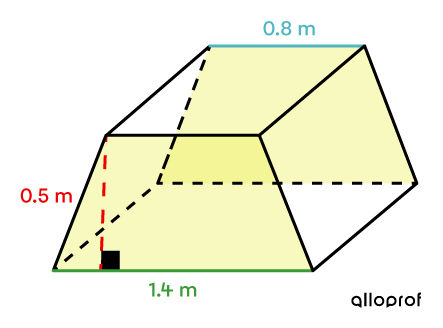
-
Apply the appropriate formula
Calculate the area of a trapezoid using the following formula: ||\begin{align} A_\text{b} &= A_\text{trapezoid} \\&=\dfrac{(\color{#3A9A38}{B} + \color{#51B6C2}{b}) \times \color{#EC0000}{h}}{2}\\&= \dfrac{(\color{#3A9A38}{1{.}4} + \color{#51B6C2}{0{.}8}) \times \color{#EC0000}{0{.}5}}{2}\\&= 0{.}55 \ \text{m}^2\end{align}|| -
Interpret the answer
Since there are 2 bases, multiply the previous result by 2: ||\begin{align} A_\text{bases} &= 0{.}55 \times 2\\&= 1{.}1 \ \text{m}^2\end{align}||
Answer: The surface area covered by the printed images (the 2 bases) is |1{.}1\ \text{m}^2.|
Regardless of the bases of the right prism, the area of its lateral faces can be calculated using the following formula.
||A_L = P_b \times h|| where ||\begin{align} A_L&=\text{Lateral area} \\ P_b &= \text{Perimeter of a base}\\ h\ &= \text{Prism height}\end{align}||
A candy company wants to sell a new chocolate bar in the following shape:
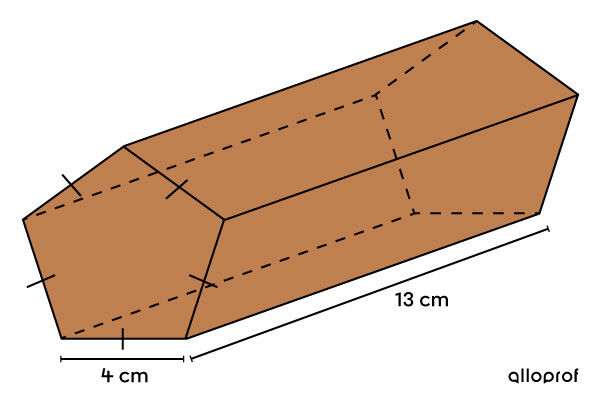
In addition, the packaging on the lateral faces requires more expensive paper. To limit the costs, determine the measurement of the lateral area.
-
Identify the solid
It is a regular pentagonal-based prism. -
Apply the formula for the lateral area of the identified solid
||\begin{align}A_L &= P_b \times h\\ &= (4 + 4 + 4 + 4 + 4) \times 13\\ &= 260 \ \text{cm}^2\end{align}|| -
Interpret the answer
The measurement of the lateral area of the chocolate bar is |260 \ \text{cm}^2.|
The formula is based on the net of the solid.
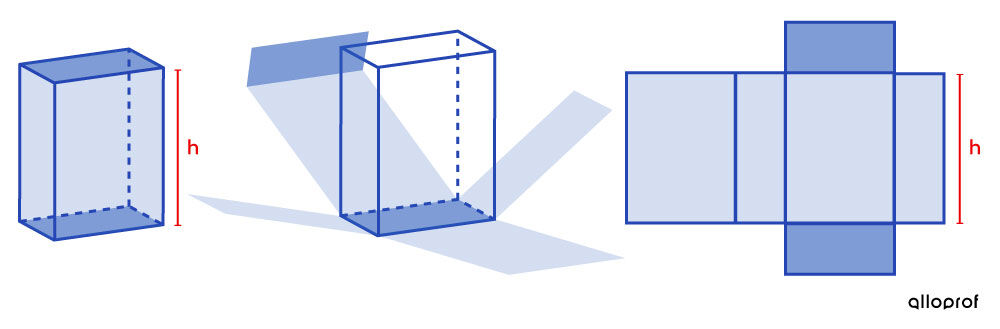
The lateral area can be drawn with a single large rectangle.
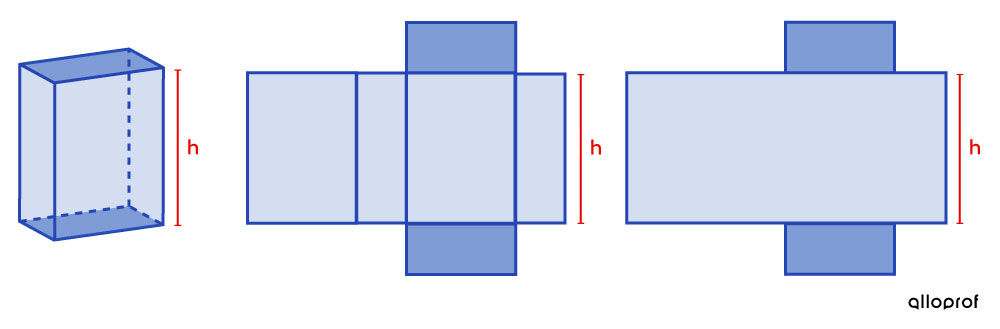
Measuring the length of the rectangle’s base is equivalent to measuring the perimeter of the prism’s base.
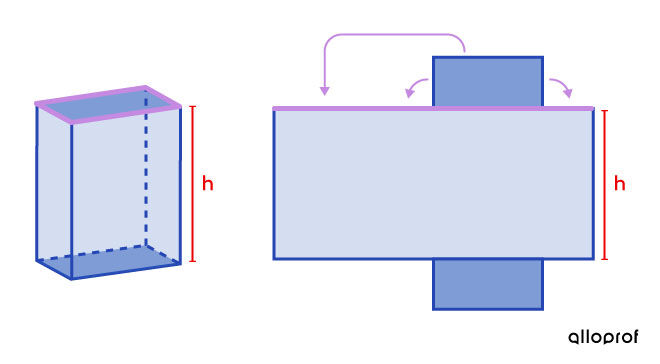
This is the reason why the perimeter of the base is included in the formula for calculating the lateral area of a prism.
Based on the word “total”, the formula associated with the area corresponds to the sum of the area of the bases and the lateral area.
||A_T = 2 A_b + A_L|| where ||A_T=\text{Total area}||
For this formula, it is important to remember that there are 2 congruent bases in a prism, i.e., |2A_b.|
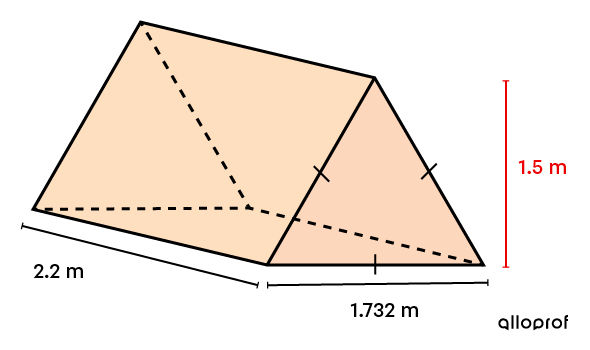
A tent needs to be coated with an aerosol product to ensure it is waterproof. However, a can of this product only covers an average area of |6 \ \text{m}^2.|
Based on the measurements in the following drawing, determine how many cans are needed to completely waterproof the tent.
-
Identify the relevant faces
The tent must be waterproofed completely. Thus, the area of the 5 faces must be calculated. -
Calculate the area of a base
Since this is a triangular prism, apply the formula for the area of a triangle. ||\begin{align} A_\text{b} &= A_\text{triangle}\\ &= \frac{b \times \color{#EC0000}{h}}{2}\\ &= \frac{1{.}732 \times \color{#EC0000}{1{.}5}}{2}\\ &= 1{.}299 \ \text{m}^2\end{align}|| -
Calculate the lateral area
Since it is a prism, apply the following formula. ||\begin{align} A_L &= P_b \times h\\ &= (1{.}732 + 1{.}732 + 1{.}732) \times 2{.}2\\ &\approx 11{.}431 \ \text{m}^2\end{align}|| -
Calculate the total area
||\begin{align} A_T &= 2 A_b + A_L \\ &= 2 \times 1{.}299 + 11{.}431 \\ &= 14{.}029 \ \text{m}^2\end{align}|| -
Interpret the answer
To determine the total number of cans to buy, we must divide |14{.}029\ \text{m}^2 \div 6\ \text{m}^2/\text{can} \approx 2{.}34\ \text{cans}.|
Answer: Since only full cans can be purchased, a total of |3| full cans are needed.
Sometimes we are looking for the measurement of a prism’s base or its height from a given area. This is called finding a missing measurement of a prism from the area. In this case, the approach is a little different, but it is still important to remember the formula for the total area of prisms.