Several solids meet the definition of a prism. First, the different parts of a prism must be recognized (i.e., bases, lateral faces, height) to identify it properly. Once this step is completed, the volume can be calculated.
To determine the three dimensional space occupied by a prism, calculate the area of a base and then multiply it by the height.
||V = A_b \times h||
where
||\begin{align} A_b &= \text{Area of a base}\\ h &= \text{height of prism}\end{align}||
To ensure they get a good deal, a camper asks about the interior space of a tent.
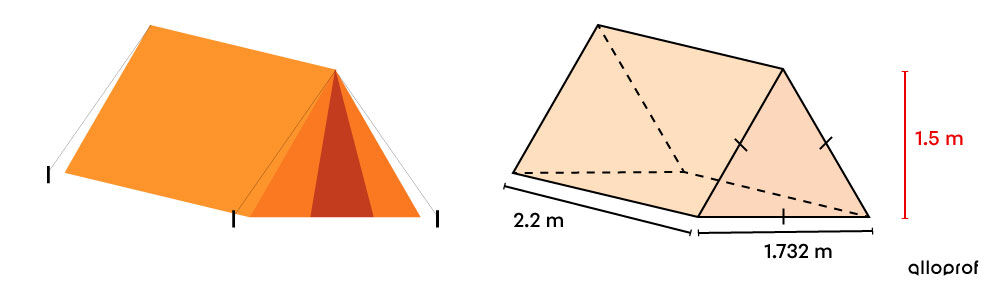
To be comfortable, the camper wants to have a minimum of |3\ \text{m}^3| of space. Considering this constraint, should they get the tent?
-
Identify the type of solid
The solid is a triangular prism. -
Apply the formula
||\begin{align} V &= A_b \times h_{Prism}\\ &= \dfrac{b \times \color{#EC0000}{h}}{2} \times h_{Prism}\\\\ &= \dfrac{1{.}732 \times \color{#EC0000}{1{.}5}}{2} \times 2{.}2\\\\ &\approx 2{.}86\ \text{m}^3\end{align}|| where |h| is the height of the triangle and |h_{Prism}| is the height of the prism. -
Interpret the answer
Since the camper is looking for a tent with a minimum capacity of |3\ \text{m}^3,| and the examined one takes up a smaller amount of space |(2{.}86\ \text{m}^3),| it would be better if they opt for another model.
Despite the simplicity of this process, be careful not to mix up the different height measurements. For example, the area of the base |h| refers to the height measurement of the base. However, when calculating the volume, |h| is the height measurement of the prism. It is a good idea to identify the prism’s height by |h_{Prism}| to avoid any confusion.
In some problems, the prism’s height is sought while the volume is given. This is called Finding a Missing Measurement of a Prism from the Volume. The approach is a little different. It is still important to remember the volume formula for prisms.