A decomposable solid is a solid that can be separated into several simpler solids.
Even though the question involves a solid, the best approach to find the area of a complex decomposable solid is to break it down into the different figures that form it. Thus, it suffices to calculate the area of each of the faces according to their respective area formulas and add them.
Since these solids are more complex, it is no longer a question of the area of the base and lateral area, but instead the total area of the solid.
What is the total area of a cube with a side measurement of |2\ \text {cm}|, connected to a pyramid with an apothem measuring |2.24\ \text {cm?}|
-
Identify the faces needed to find the total area
In the example, we must consider the 4 triangles which form the lateral faces of the pyramid, the 4 squares which form the lateral faces of the cube, and the square which forms the base of the cube. -
Apply the appropriate formulas
||\begin{align} A_\text{total} &= 4 \times \color{#333FB1}{A_\text{triangle}} + 4 \times \color{#EC0000}{A_\text{square}}+ \color{#3A9A38}{A_\text{square}} \\ &= 4 \times \color{#333FB1}{\dfrac{b\times h}{2}} + 4 \times \color{#EC0000}{c^2} + \color{#3A9A38}{c^2} \\ &= 4 \times \color{#333FB1}{\dfrac{2 \times 2{.}24}{2}} + 4 \times \color{#EC0000}{2^2} + \color{#3A9A38}{2^2}\\ &= \color{#333FB1}{8{.}96} + \color{#EC0000}{16} + \color{#3A9A38}{4}\\ &= 28{.}96\ \text{cm}^2 \end{align}|| -
Interpret the answer
The total area of the solid is |28{.}96\ \text{cm}^2.|
Not only is it important to consider the faces that disappear during the construction of a solid, but special attention must be given to the order of operations. Many operations are involved in the process, so proceeding methodically is essential so as not to forget anything important.
Solids can be stacked so that only part of a surface disappears.
What is the area of the following solid?
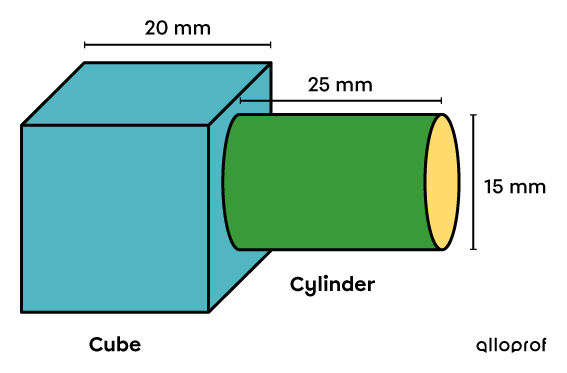
-
Identify the faces needed to calculate the total area
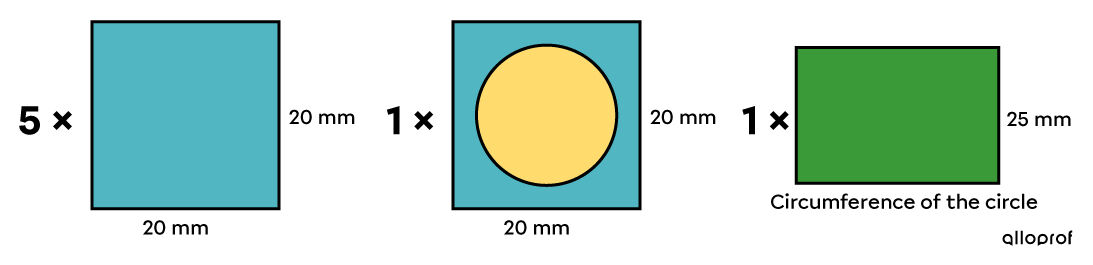
Looking at this solid, we can identify 5 complete squares and a rectangle that forms the lateral face of the cylinder. Also, when we associate the visible base of the cylinder with the incomplete square to which the cylinder is attached, we obtain a square with the same dimension as the other 5.
-
Apply the appropriate formulas
Calculate the area of the 6 squares and a rectangle. ||\begin{align} A &= 6 \times \color{#51b6c2}{A_\text{square}} + \color{#3a9a38}{A_\text{cylinder lateral}} \\ &= 6 \times \color{#51b6c2}{c^2} +\color{#3a9a38}{2\pi r h}\\ &= 6 \times \color{#51b6c2}{20^2} + \color{#3a9a38}{2 \pi (15 \div 2) \times 25}\\ &\approx \color{#51b6c2}{2\ 400} + \color{#3a9a38}{1\ 178{.}1}\\ &\approx 3\ 578{.}1\ \text{mm}^2 \end{align}|| -
Interpret the answer
The area of the decomposable solid is approximately |3\ 578{.}1\ \text{mm}^2.|
By proceeding in this manner, it is easy to identify the unknowns when finding a missing measurement of a decomposable solid from the area.
In some situations, some sections of a solid are removed to create an empty space inside. When this happens, these solids are non-convex.
At first glance, this kind of solid may seem to have a smaller surface area since some sections are removed. Nevertheless, the following example shows that the approach used is similar to the one for convex decomposable solids.
What is the total area of the solid?
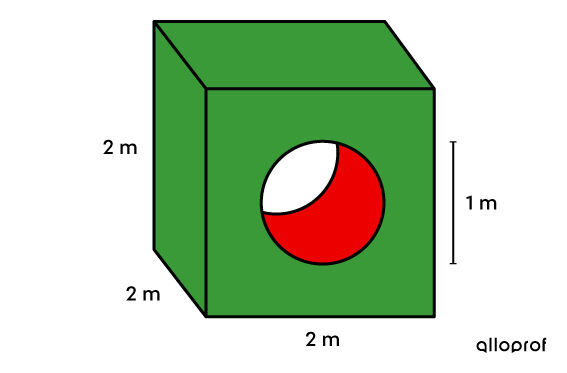
-
Identify the faces needed to calculate the total area
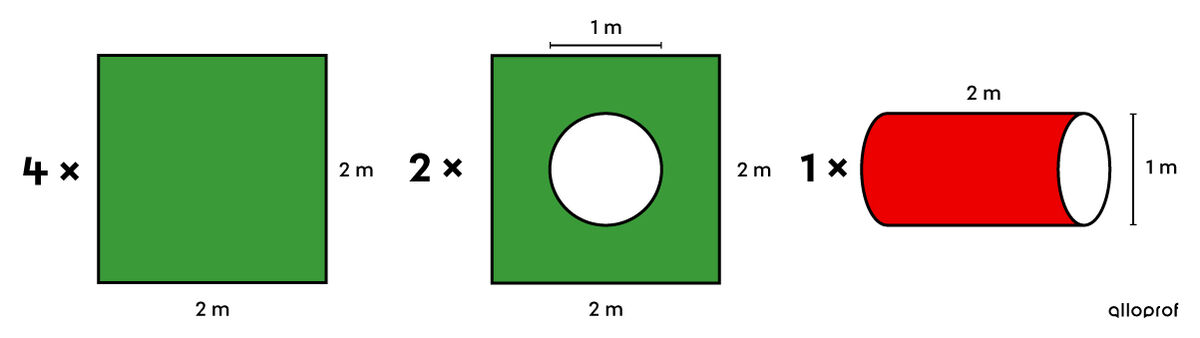
In the example, we must consider the 6 squares used for the faces of the cube. However, we must remove the area of a circle from the surface of two of the squares. Finally, the curved surface inside the cube corresponds to the lateral face of a cylinder.
-
Apply the appropriate formulas
||\begin{align} A &=& &4 \times \color{#3a9a38}{A_\text{square}}&&+&& 2 \left(\color{#3a9a38}{A_\text{square}} - A_\text{disc}\right) &&+&& \color{#ec0000}{A_{L\ \text{cylinder}}}\\ &=&& 4 \times \color{#3a9a38}{c^2} &&+&& 2 \left(\color{#3a9a38}{c^2} - \pi r^2\right) &&+&& \color{#ec0000}{2 \pi r h}\\ &=&& 4 \times \color{#3a9a38}{2^2} &&+&& 2 \left(\color{#3a9a38}{2^2} - \pi \left(1 \div 2\right)^2\right) &&+&& \color{#ec0000}{2 \pi (1 \div 2) \times 2}\\ &\approx&& 16 &&+&& 2 \left( 4 - 0{.}79\right) &&+&& 6{.}28 \\ &\approx &&28{.}7 \ \text{m}^2 \end{align}|| -
Interpret the answer
The total area of the solid is approximately |28{.}7 \ \text{m}^2.|
Note : among all the measurements given, the diameter measurement and the radius measurement should not be confused. In the example, |1 \ \text{m}| is the measurement of the diameter. To find the radius, simply use the rule |r = \dfrac{d}{2}.|
Since the solid is complex, it is normal for the process to be a little longer than for a non-complex solid. However, by proceeding in this manner, and by working logically one step at a time, it will be easier to identify the unknowns when finding a missing measurement of a decomposable solid from its given area.