To successfully calculate a missing measure in a decomposable or truncated solid using the area, the formulas for the area of plane figures are useful. The approach is more complex than the one for simple solids like prisms and pyramids, because the number of plane figures used in the construction of a decomposable solid is greater. To understand the examples in this concept sheet better, the following is an example of the steps used.
-
Determine the area formula to use.
-
Identify the missing measurement(s), using a variable.
-
Associate the area of each figure with a numerical value or an algebraic expression.
-
Create an equation based on the context.
-
Solve the equation.
-
Interpret the answer according to the context.
To increase marketplace visibility, a company working in the pet supply industry wants to market a new toy for dogs. To attract customers to the new product, it plans to cover the toy with a product that has a smell and taste dogs love.
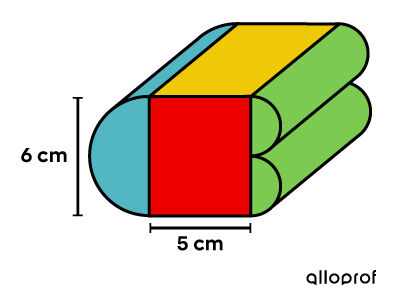
After a few calls, the company finds a supplier willing to sell a product for |$0.02 / \text{cm}^2| of the surface area to be covered. To maximize profits, the company will invest |$9.20| to cover each toy with the product.
To respect the profit margin, what should be the toy’s length?
-
Determine the area formula to use
Through proportionality, we determine the following.
||\begin{align} \dfrac{$0.02}{1 \ \text{cm}^2} &= \dfrac{$9.20}{\text{Total area}} \\\\ \text{Total area} &= \dfrac{ 9.20 \times 1}{0.02}\\ &= 460 \ \text{cm}^2\end{align}|| -
Identify the missing measurement using a variable
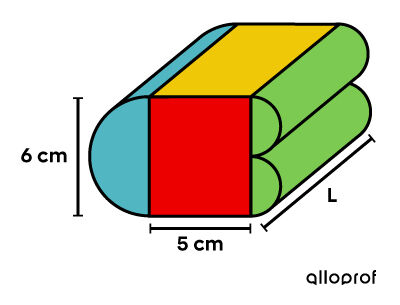
-
Find the area of each surface
||\begin{align} \color{#ec0000}{A_\text{rectangles}} &= (5 \times 6) \times 2\\ &= \color{#ec0000}{60 }\\\\ \color{#EFC807}{A_\text{rectangles}} &= (5 \times L) \times 2\\ &= \color{#EFC807}{10L}\\\\ \color{#51B6C2}{A_\text{half-cylinder}} &= \dfrac{\pi (6 \div 2)^2} {2} \times 2+ \left( \dfrac{6 \pi }{2}\right) \times L\\ &\approx \color{#51B6C2}{28.27 + 9.42 L}\\\\ \color{#7CCA51}{A_\text{2 half-cylinders}} &= \dfrac {\pi (6 \div 4)^2}{2} \times 4 + \dfrac{\pi (6 \div 2)}{2} \times L \times 2\\ &\approx \color{#7CCA51}{14.14 + 9.42 L}\end{align}|| -
Create an equation according to the context
||\begin{align} \text{Total area} &= \text{Sum of all surface areas}\\ 460 &= \color{#ec0000}{60} + \color{#EFC807}{10L} + \color{#51B6C2}{28.27 + 9.42L} + \color{#7CCA51}{14.14 + 9.42L}\\ 460 &= 28.84 L + 102.41\end{align}|| -
Solve the equation
||\begin{align}460 \color{#ec0000}{-102.41} &= 28.84L + 102.41 \color{#ec0000}{-102.41} \\ \color{#ec0000}{\dfrac{\color{black}{357.59}}{28.84}} &= \color{#ec0000}{\dfrac{\color{black}{28.84L}}{28.84}}\\ 12.40 &\approx L\end{align}|| -
Interpret the answer according to the context
The length of the toy should be about |12.40 \ \text{cm}.|
In general, it is a matter of properly identifying the unknown and using the appropriate formulas to create an equation that summarizes the situation. Once the equation is solved, we simply interpret the answer.
To find the missing measurements according to the area of complex solids with second-degree equations, the procedure is similar to the one involving first-degree equations. However, the methods for solving the problem in step 5 will be a little different. In general, we can rely on factorization by the product-sum technique or the quadratic formula to solve such an equation.
A company specializes in the manufacture of crampons. To meet product demand, it needs to build a crampon that resembles the following.
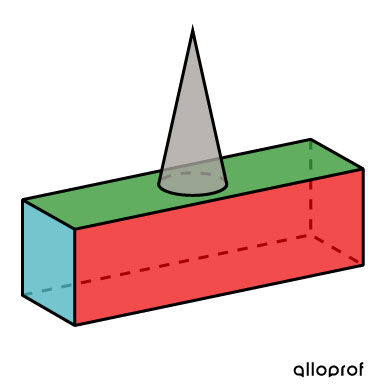
The crampon also must meet the following specifications.
-
The base’s length must measure |10\ \text{mm}| more than the cone’s apothem.
-
The base’s width must measure |4\ \text{mm}| less than the cone’s apothem.
-
The prism’s height must measure exactly |6\ \text{mm}.|
-
The measure of the cone’s radius must be exactly |2\ \text{mm}.|
-
The total area of a crampon must be |600\ \text{mm}^2.|
What are the precise measurements of each of the crampon’s dimensions?
-
Determine the total area
The total area is stated as |600\ \text{mm}^2.| -
Identify the measurements using a variable or an algebraic expression
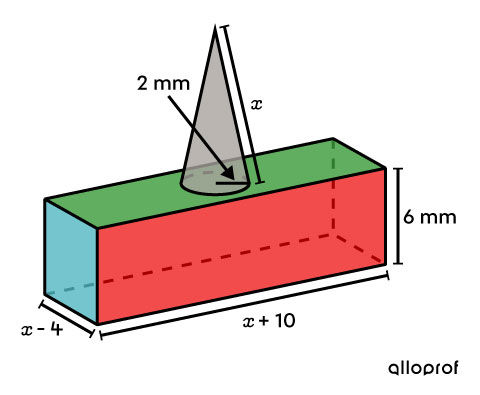
-
Find the area of each surface
||\begin{align} \color{#51b6c2}{A_\text{rectangles}} &= \big((x-4) \times 6\big) \times 2\\ &=(6x-24)\times 2\\
&= \color{#51b6c2}{12x - 48}\\\\
\color{#ec0000}{A_\text{rectangles}} &= \big((x+10) \times 6\big)\times 2\\ &=(6x+60)\times 2\\
&= \color{#ec0000}{12x + 120}\\\\
A_\text{bottom rectangle} &= (x+10)\times (x-4)\\ &=x^2+10x-4x-40\\
&= x^2 + 6x - 40\\\\
\color{#3a9a38}{A_\text{rectangle}} &= (x+10) \times (x-4) - \pi (2)^2\\
&= x^2-4x+10x-40 - 4\pi\\
&\approx \color{#3a9a38}{x^2 + 6x-52.57}\\\\
\color{#a8a39e}{A_\text{cone}} &= \pi r a\\
&= \pi \times 2 \times x\\
&\approx 6.28x\\
&\color{#a8a39e}{\approx 6.28x} \end{align}|| -
Create an equation
||\begin{align} \text{Total area} &= \text{Sum of all surface areas}\\ 600 &= \color{#51b6c2}{12x-48} + \color{#ec0000}{12x+120} + x^2 + 6x - 40 + \color{#3a9a38}{x^2+6x-52.56} +\color{#a8a39e}{6.28x}\end{align}|| -
Solve the equation
||\begin{align} 600 &= 2x^2+42.28x -20.26\\
0 &= 2x^2+42.28x - 620.26\\\\
\{x_1, x_2\} &= \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\
\{x_1, x_2\} &= \frac{-(42.28) \pm \sqrt{42.28^2-4 (2)(-620.26)}}{2 \times 2}\\\\ x_1 &\approx -31.11 \ \text{et} \ x_2 \approx 9.97\end{align}|| -
Interpret the answer according to the context
We want a length measure, so we only consider the positive value, i.e., |x_2 \approx 9.97.|
The missing dimensions are the following.
||\begin{align} \text{Length} &= x+10\\
&=9.97+10\\
&= 19.97\ \text{mm}\\\\
\text{Width} &= x-4\\
&=9.97-4\\
&= 5.97\ \text{mm}\\\\
\text{Apothem} &= x\\
&=9.97\ \text{mm}
\end{align}||
Due to its particular construction, a truncated solid is often associated with a decomposable solid. In fact, it is a solid with a portion removed. In some cases, it is necessary to establish a proportion between the measurements of the complete solid and the truncated part. In other cases, it’s enough to analyze each of the solid’s faces and decompose them appropriately to find polygons with which we are more familiar. We can apply the first method to truncated cones, as in the following example.
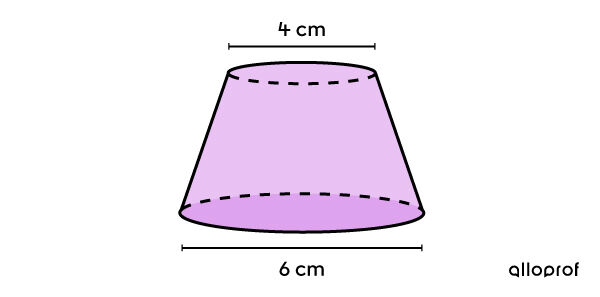
The following rubber stopper has a total area of |105.61\ \text{cm}^2.| What is the height of the stopper if the diameter of the small circle is |4\ \text{cm}| and the large one is |6\ \text{cm}?| The stopper is a truncated cone where the 2 bases are parallel circles.
-
Determine the total area
The total area is |\text{A}_{\text{Total}}=105.61\ \text{cm}^2.| -
Identify the missing measurement(s)
We represent the whole cone to visualize the situation better.
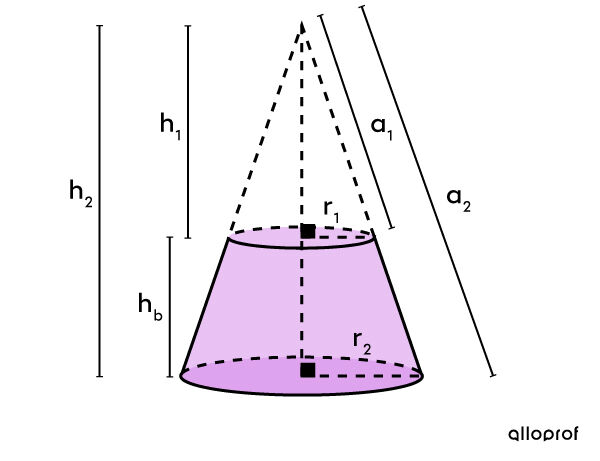
There are several missing measurements, namely the height of the truncated cone |(h_1),| the apothem of the truncated cone |(a_1),| the height of the complete cone |(h_2),| the apothem of the complete cone |(a_2),| and the height of the stopper |(h_s).| We must assign the variable |x| to one of them. We assume |x=a_1.|
We find both radii.
|| \begin{align}r_1 = 4 \ \text{cm} \div 2 = 2 \ \text{cm}\\
r_2 = 6 \ \text{cm} \div 2 = 3 \ \text{cm} \end{align}||
In a truncated cone, as in a truncated pyramid, the corresponding sides are proportional.
||\dfrac{\text{radius}_1}{\text{radius}_2} = \dfrac{\text{apothem}_1}{\text{apothem}_2} = \dfrac{\text{height}_1}{\text{height}_2}||
||\begin{align} \dfrac{r_1}{r_2}&=\dfrac{a_1}{a_2}\\\\ \dfrac{2}{3}&=\dfrac{x}{a_2}\\\\ \Rightarrow\ a_2&=\dfrac{3x}{2}\\ &=1.5x \end{align}||
-
Find the area of each surface
||\begin{align}A_{\text{small base}}&=\pi r_1^2\\&=\pi (2)^2\\ &=4\pi \end{align}|| ||\begin{align}A_{\text{large base}}&=\pi r_2^2\\&=\pi (3)^2\\ &=9\pi \end{align}||To calculate the lateral area of the truncated cone |(A_{\text{L trunc}}),| we must subtract the lateral area of the truncated cone |(A_{L1})| from the lateral area of the whole cone |(A_{L2}).|
||\begin{align}A_{L1}&=\pi r_1a_1\\&=\pi (2) (x)\\&\approx6.28x \end{align}|| ||\begin{align}A_{L2}&=\pi r_2a_2\\&=\pi (3) (1.5x)\\&\approx14.14x \end{align}|| ||\begin{align}A_{L\ \text{trunc}}&=A_{L2}-A_{L1}\\&=4.5\pi x - 2\pi x\\&=2.5\pi x\\&\approx7.85x \end{align}||
-
Create an equation according to the context
||\begin{align}A_{\text{L trunc}}&=A_{\text{stopper}}-A_{\text{small base}}-A_{\text{large base}}\\2.5 \pi x &=105.61-4\pi-9\pi \\ 2.5 \pi x &\approx 64.77 \end{align}|| -
Solve the equation
||\begin{align} \color{#ec0000}{\dfrac{\color{black}{2.5 \pi x}}{2.5\pi}} &\approx \color{#ec0000}{\dfrac{\color{black}{64.77}}{2.5\pi}} \\ x &\approx 8.25\ \text{cm} = a_1 \end{align}|| -
Interpret the answer according to the context
Now, we have the value of |x.| Next, we must use this measure to calculate the height of the truncated pyramid |(h_1).| We use the Pythagorean Theorem on the triangle formed by |a_1,| |h_1| and |r_1.|||\begin{align} {h_1}^2 &= {a_1}^2 - {r_1}^2 \\ h_1 &= \sqrt{8.25^2 - 2^2}\\ h_1 &\approx 8\ \text{cm} \end{align}||
To calculate |h_2,| we can rely on the fact that the corresponding sides are proportional.
||\begin{align} \dfrac{r_1}{r_2} &= \dfrac{h_1}{h_2} \\\\ \dfrac{2}{3} &= \dfrac{8}{h_2} \\\\ \Rightarrow\ h_2 &= \dfrac{3\times 8}{2} \\ h_2 &= 12\ \text{cm} \end{align}||
Lastly, we determine the height of the stopper.
||\begin{align}h_b&=h_2-h_1\\ &=12-8\\&=4\ \text{cm}\end{align}||
The next example shows a situation with a truncated prism.
To renovate an apartment building, the owner decides to replace the exterior siding and change the roof’s structure. Instead of a flat roof, he wants a roof sloped on two sides.
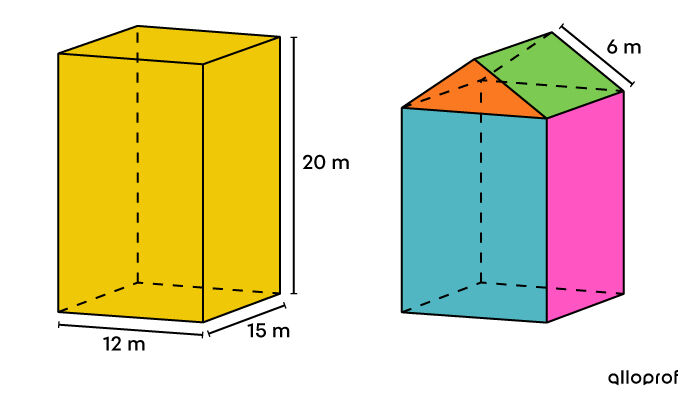
To cover the cost of the new siding, the budget is | $30 \ 000.| The construction material costs |$27.70 /\text{m}^2.| What should be the height of the building’s new roof with two sloped sides?
-
Determine the total area
||\begin{align} \text{Total area} &= $30 \ 000 \div $27.70/\text{m}^2 \\ &\approx 1 \ 083.03 \ \text{m}^2 \end{align}|| -
Identify the missing measure
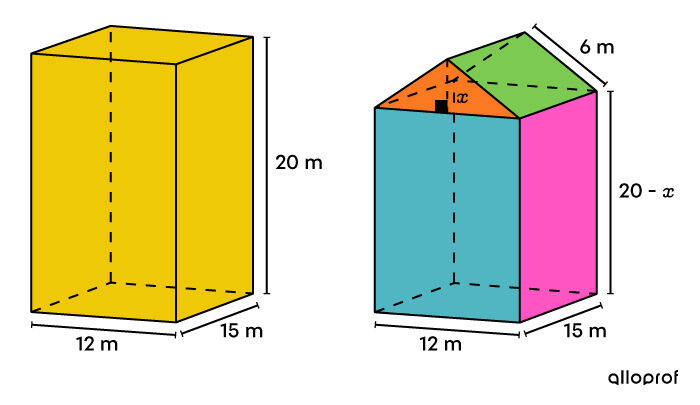
-
Find the area of each surface
||\begin{align} \color{#51b6c2}{A_\text{rectangles}} &= \big(12 (20-x)\big) \times 2 \\
&= \color{#51b6c2}{480 - 24x} \\\\
\color{#ff55c3}{A_\text{rectangles}} &= \big(15 (20-x)\big)\times 2 \\
&= \color{#ff55c3}{600 - 30x} \\\\
\color{#fa7921}{A_\text{triangles}} &= \left(\dfrac{12 \times x}{2}\right) \times 2 \\
&= \color{#fa7921}{12x}\\\\
\color{#7cca51}{A_\text{rectangles}} &= (6 \times 15) \times 2\\
&= \color{#7cca51}{180} \end{align}|| -
Create an equation according to the context
||\begin{align} \text{Total area} &= \text{Sum of all the surface areas}\\
1 \ 083.03 &= \color{#51b6c2}{480 - 24x} + \color{#ff55c3}{600 - 30x} + \color{#fa7921}{12x} + \color{#7cca51}{180}\end{align}|| -
Solve the equation
||\begin{align} 1 \ 083.03 &= 1\ 260 - 42x \\ 1 \ 083.03 \color{#ec0000}{-1\ 260} &= 1\ 260 \color{#ec0000}{-1\ 260} - 42x \\ \color{#ec0000}{\dfrac{\color{black}{-176.97}}{-42}} &= \color{#ec0000}{\dfrac{\color{black}{-42x}}{-42}} \\ 4.21 &\approx x \end{align}|| -
Interpret the answer according to the context
The height of the roof should be approximately |4.21 \ \text{m}.|
Since we are working in three dimensions, there are occasionally missing or hidden sections of the solid. Regardless, we can generally break down a non-convex (concave) solid into the different plane figures of which it consists.
The approach could be similar to the following.
As a hobby, Natasha makes customized cakes. To respect her recent client’s budget, she has |$11| remaining to invest on icing for the cake.
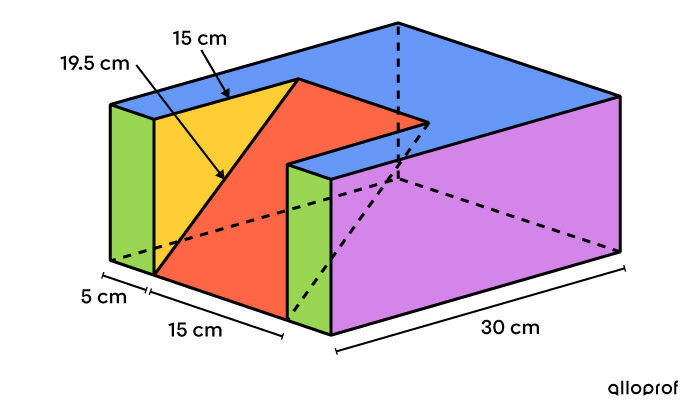
If it costs her |$0.50/ \text{dm}^2| for the necessary ingredients, what should be the height of the cake?
-
Determine the total area
||\begin{align} \dfrac{$0.5}{1\ \text{dm}^2} &= \dfrac{$11}{?\ \text{dm}^2} \\\\ ? &= \dfrac{11\times 1}{0.5} \\ &= 22\ \text{dm}^2 \\ &= 2\ 200\ \text{cm}^2\end{align}|| -
Identify the missing measurement(s) using a variable
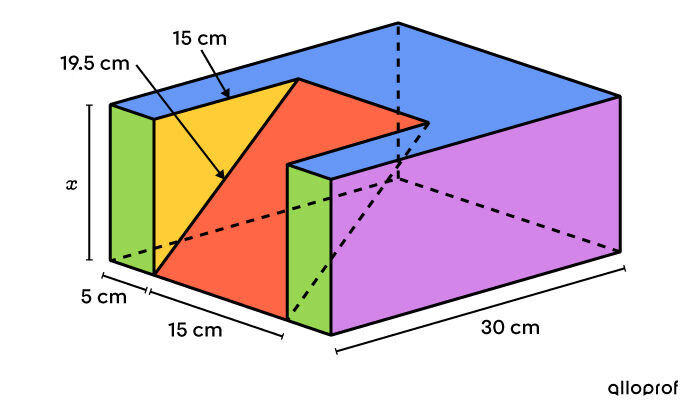
-
Find the area of each surface
Before finding the surface area of all the faces, it’s important to keep the context in mind. Because it’s a cake, there is no icing on the bottom. Therefore, there’s no need to calculate the area of the rectangle on the bottom of the cake.
||\begin{align} \color{#3b87cd}{A_\text{top}} &= (5 \times 15) \times 2 + (30-15) (5 + 15 + 5) \\ &= 150 + 375\\ &= \color{#3b87cd}{525 \ \text{cm}^2} \\\\ \color{#7cca51}{A_\text{rectangles}} &= (5 \times x) \times 2 \\ &= \color{#7cca51}{10 x} \\\\ A_\text{rectangle behind} &= (5 + 15 + 5) \times x \\ &= 25x \\\\ \color{#c58ae1}{A_\text{rectangles}} &= (30 \times x) \times 2 \\ &= \color{#c58ae1}{60x} \\\\ \color{#efc807}{A_\text{triangles}} &= \left(\dfrac{15 \times x}{2}\right) \times 2 \\ &= \color{#efc807}{15x}\\\\ \color{#ec0000}{A_\text{rectangle}} &= 15 \times 19.5 \\ &= \color{#ec0000}{292.5\ \text{cm}^2} \end{align}|| -
Create an equation according to the context
||\begin{align} \text{Total area} &=\text{Sum of all the surface areas}\\ 2 \ 200 &=\color{#3b87cd}{525} + \color{#7cca51}{10x} + 25x + \color{#c58ae1}{60x} + \color{#efc807}{15x} + \color{#ec0000}{292.5}\end{align}|| -
Solve the equation
||\begin{align} 2 \ 200 &= 110x + 817.57 \\ 2 \ 220 \color{#ec0000}{-817.57} &= 110x +817.57 \color{#ec0000}{-817.57} \\ \color{#ec0000}{\dfrac{\color{black}{1\ 382.43}}{110}} &= \color{#ec0000}{\dfrac{\color{black}{110x}}{110}} \\ 12.57 &\approx x \end{align}|| -
Interpret the answer according to the context
The cake’s height should be about |12.57 \ \text{cm}.|
To validate your understanding of missing measurements in solids, consult the following interactive CrashLesson:
