Un solide décomposable est un solide pouvant être séparé en plusieurs solides plus simples.
Même s'il est question d'un solide, la démarche privilégiée est de le décomposer selon les différents types de figures qui le composent. Ainsi, il suffit de calculer l'aire de chacune des faces selon leur formule d'aire respective et de les additionner.
Puisque ces solides sont plus complexes, il ne sera plus question d'aire des bases et d'aire latérale, mais simplement d'aire totale du solide.
Quelle est l'aire totale d'un cube de 2 cm de côté surmonté d'une pyramide dont l'apothème mesure 2,24 cm?
-
Identifier les faces concernées
Dans le cas présent, il faut considérer les 4 triangles qui forment les faces latérales de la pyramide, les 4 carrés qui forment les faces latérales du cube et le carré qui forme la base du cube. -
Appliquer les formules appropriées
||\begin{align} A_\text{totale} &= 4 \times \color{#333FB1}{A_\text{triangle}} + 4 \times \color{#EC0000}{A_\text{carré}}+ \color{#3A9A38}{A_\text{carré}} \\ &= 4 \times \color{#333FB1}{\dfrac{b\times h}{2}} + 4 \times \color{#EC0000}{c^2} + \color{#3A9A38}{c^2} \\ &= 4 \times \color{#333FB1}{\dfrac{2 \times 2{,}24}{2}} + 4 \times \color{#EC0000}{2^2} + \color{#3A9A38}{2^2}\\ &= \color{#333FB1}{8{,}96} + \color{#EC0000}{16} + \color{#3A9A38}{4}\\ &= 28{,}96\ \text{cm}^2 \end{align}|| -
Interpréter la réponse
L'aire totale de ce solide est de |28{,}96\ \text{cm}^2.|
En plus des faces qui disparaissent dans la construction du solide, il faut également porter une attention particulière à la priorité des opérations. En effet, il y a beaucoup d'opérations qui sont impliquées dans la démarche. Il faut s'assurer de procéder de façon méthodique afin de ne rien oublier.
Les solides peuvent être superposés de façon à ce que seule une partie de leur surface disparaisse.
Quelle est l'aire de ce solide?

-
Identifier les faces concernées
Pour ce solide, on peut identifier les 5 carrés complets et le rectangle qui forme la face latérale du cylindre. De plus, quand on associe la base visible du cylindre avec le carré incomplet auquel le cylindre est collé, on obtient un carré de même dimension que les 5 autres.
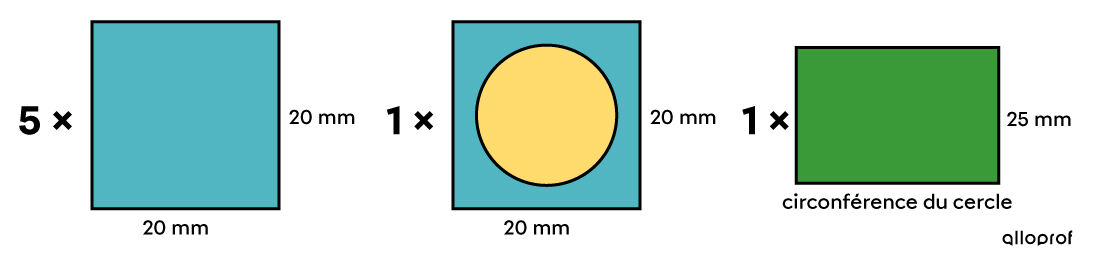
-
Appliquer les formules appropriées
Il suffit de calculer l'aire de 6 carrés et d'un rectangle.||\begin{align} A &= 6 \times \color{#51b6c2}{A_\text{carré}} + \color{#3a9a38}{A_\text{latérale cylindre}} \\ &= 6 \times \color{#51b6c2}{c^2} +\color{#3a9a38}{2\pi r h}\\ &= 6 \times \color{#51b6c2}{20^2} + \color{#3a9a38}{2 \pi (15 \div 2) \times 25}\\ &\approx \color{#51b6c2}{2\ 400} + \color{#3a9a38}{1\ 178{,}1}\\ &\approx 3\ 578{,}1\ \text{mm}^2 \end{align}|| -
Interpréter la réponse
L'aire de ce solide décomposable est d'environ |3\ 578{,}1\ \text{mm}^2.|
En procédant de cette façon, on peut mieux identifier les inconnues lorsqu'on doit trouver une mesure manquante d'un solide décomposable à partir de l'aire.
Il peut arriver que certaines portions soient littéralement enlevées du solide afin de créer un espace vide à l'intérieur de ce dernier. Dans ce cas, il est question de solides non convexes.
En apparence, ce genre de solide semble posséder une plus petite surface puisque certaines sections sont retirées. Par contre, l'exemple suivant montre que la démarche est semblable à celle utilisée pour les solides décomposables convexes.
Quelle est l'aire totale de ce solide?
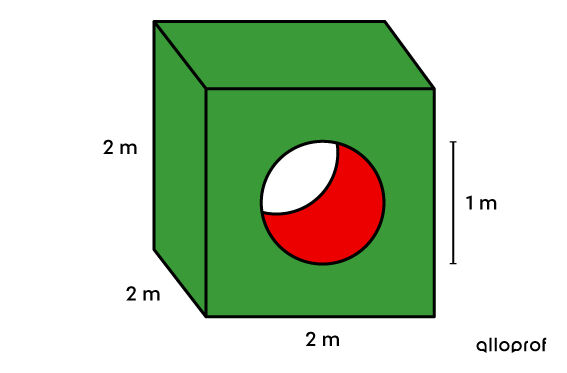
-
Identifier les faces concernées
Dans le cas présent, il faut considérer les 6 carrés utilisés pour les faces du cube. Or, pour 2 d'entre eux, on doit enlever la surface équivalente à celle d'un disque. Finalement, la surface courbe qui est à l'intérieur du cube correspond à la face latérale d'un cylindre.
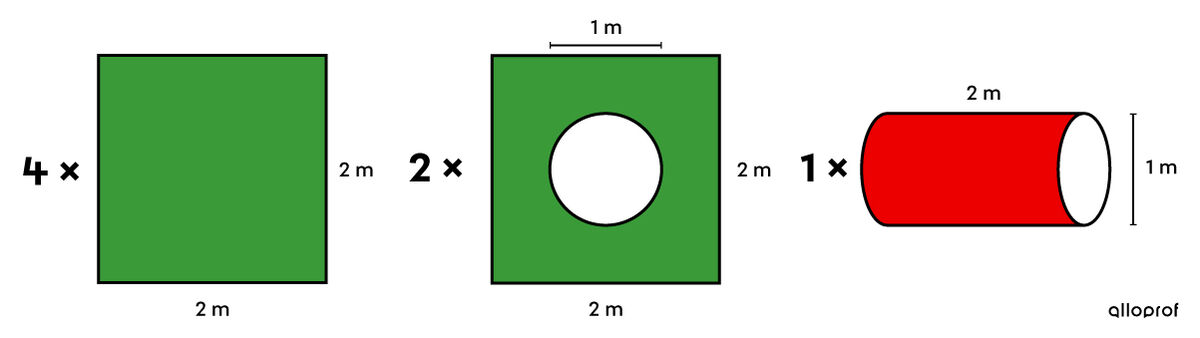
-
Appliquer les formules appropriées
||\begin{align} A &=& &4 \times \color{#3a9a38}{A_\text{carré}}&&+&& 2 \left(\color{#3a9a38}{A_\text{carré}} - A_\text{disque}\right) &&+&& \color{#ec0000}{A_{L\ \text{cylindre}}}\\ &=&& 4 \times \color{#3a9a38}{c^2} &&+&& 2 \left(\color{#3a9a38}{c^2} - \pi r^2\right) &&+&& \color{#ec0000}{2 \pi r h}\\ &=&& 4 \times \color{#3a9a38}{2^2} &&+&& 2 \left(\color{#3a9a38}{2^2} - \pi \left(1 \div 2\right)^2\right) &&+&& \color{#ec0000}{2 \pi (1 \div 2) \times 2}\\ &\approx&& 16 &&+&& 2 \left( 4 - 0{,}79\right) &&+&& 6{,}28 \\ &\approx &&28{,}7 \ \text{m}^2 \end{align}|| -
Interpréter la réponse
L'aire totale de ce solide est d'environ |28{,}7 \ \text{m}^2.|
Remarque : Parmi toutes les mesures données, il ne faut pas confondre la mesure du diamètre et celle du rayon. Dans cet exemple, |1 \ \text{m}| est la mesure du diamètre. Pour trouver le rayon, il suffit d'utiliser l'égalité |r = \dfrac{d}{2}.|
Puisque le solide est complexe, il est normal que la démarche soit un peu plus longue que pour un solide non complexe. Par contre, en procédant de cette façon, soit en structurant bien sa démarche en une seule et même étape, on peut mieux identifier les inconnues lorsqu'on veut trouver une mesure manquante d'un solide décomposable selon son aire.