First, identify the different parts (i.e., base, apothem, height) of a pyramid. Its volume can then be calculated.
To determine the three-dimensional space occupied by a pyramid, first consider the area of its base and then multiply it by its height. Finally, divide it by 3.
||V = \dfrac{A_b \times h}{3}||
where
||\begin{align} A_b &= \text{Area of a base}\\ h &= \text{height of the pyramid}\end{align}||
In Quebec City, part of a commercial building is built like a square pyramid.

To comply with regulations, the pyramid section of the building has a base with a perimeter of |160\ \text{m}| and a height of |15\ \text{m}.| |70\ \%| of the space is reserved for administrative offices. How much space do the administrative offices occupy?
-
Identify the type of solid
It is a square pyramid. -
Apply the formula
Since the base is square, we can determine that one side measures |160 \div 4=40\ \text{m}.|
Thus, ||\begin{align} V &=\dfrac{A_b \times h}{3}\\\\&= \dfrac{s^2\times h}{3} \\\\&= \dfrac{40^2 \times 15}{3}\\\\&= 8\ 000\ \text{m}^3 \end{align}|| -
Interpret the answer
Since we are interested in |70\ \%| of the space, the following is obtained.
||70\ \% \times 8\ 000 = 5\ 600\ \text{m}^3||Thus, the administrative offices occupy |5\ 600 \ \text{m}^3.|
Some problems require finding the base measurement or the height of a pyramid when the volume is given. This is called finding a missing measurement of a pyramid from a given volume. In this case, the approach is a little different, but it is still essential to remember the volume formula associated with pyramids.
When looking at a pyramid’s construction, we see that it is mainly composed of triangles. This characteristic can be used when it is time to find the measurement of the height or apothem.
There is no formula for calculating the height of a pyramid directly from its apothem. However, a well-known formula in the field of mathematics can be used: the Pythagorean Theorem.
Finding the height of a pyramid from the apothem
In the case of a right pyramid, a right triangle is obtained by drawing the height from the apex and joining it to the centre of the base. This height is called the apothem of the pyramid.
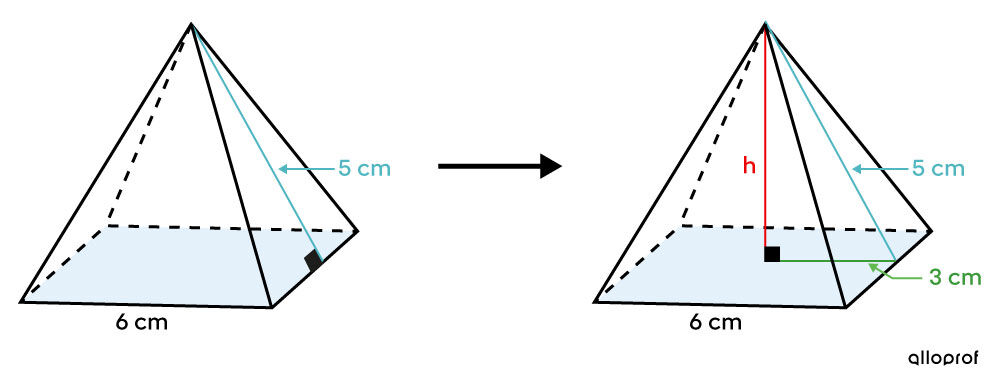
Since the pyramid’s height ends at the centre of its base, and it is a right pyramid, the measurement of the leg is half the measurement of the side of the base.
Associating the measurement of one leg with half of one side of the base, the other leg with the pyramid’s height, and the apothem with the hypotenuse enables us to use the Pythagorean Theorem.
||\begin{align} \color{#3A9A38}{a}^2 + \color{#EC0000}{b}^2 &= \color{#51B6C2}{c}^2\\\\ \color{#3A9A38}{3}^2 + \color{#EC0000}{h}^2 &= \color{#51B6C2}{5}^2\\ \color{#EC0000}{h}^2 &= 16\\ \color{#EC0000}{h} &= 4 \ \text{cm}\end{align}||
If the measurement of the apothem from the height is sought, the Pythagorean Theorem must be used.