||V_\text{cube} = s^3||
where
||s = \text{side}||
Note: The side measurement of a cube is the length of any edge.
Using the previous formula, the space occupied by a cube can be calculated regardless of the situation.
To transport dice to a polishing company, a casino wants to package 200 dice in five identical boxes. What will be the volume of one of the boxes?
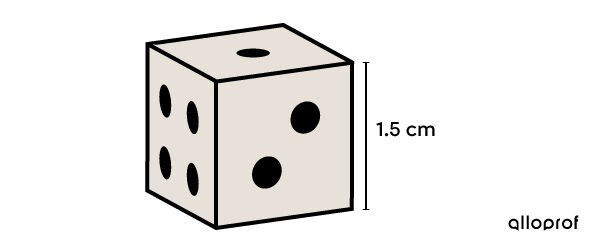
-
Identify the type of solid
It is a cube. Therefore, use formula for the volume: |V = s^3.|
-
Apply the formula
||\begin{align} V &= s^3\\ &= 1{.}5^3\\ &= 3{.}375 \ \text{cm}^3\end{align}||
-
Interpret the answer
Since there are |200| dice to move:
||\dfrac {3{.}375\ \text{cm}^3}{1\ \text{die}} \times 200\ \text{dice} = 675\ \text{cm}^3|| Finally, package the |675 \ \text{cm}^3| in |5| identical boxes:
||675\ \text{cm}^3 \div 5\ \text{boxes} = 135\ \text{cm}^3 / \text{box}|| Thus, each box should have a volume of |135\ \text{cm}^3.|
In other situations, the measure of a side is sought while the volume is given. This is called Finding a Missing Measurement of a Cube from the Volume. The approach is a little different, but it is still important to remember the formula for the volume of a cube.