A polygon is a plane figure that is formed by a closed broken line with at least 3 sides.
Working with polygons is easier with the knowledge of certain key terms. Also, other related notions can be used as well.
Some segments in a polygon have special names and characteristics. We can use the properties of the segments to clearly define the various types of polygons.
-
The length |(L)| is the size of the object’s largest dimension.
-
The width |(l)| is the size of the object’s smallest dimension.

It is also possible to refer to the sides of the rectangle using the concepts of base and height.
-
The base |(b| or |B)| is a segment from which a height is perpendicularly measured.
-
The height |(h)| is the shortest distance between 2 parallel sides or between a vertex and the base opposite the vertex.
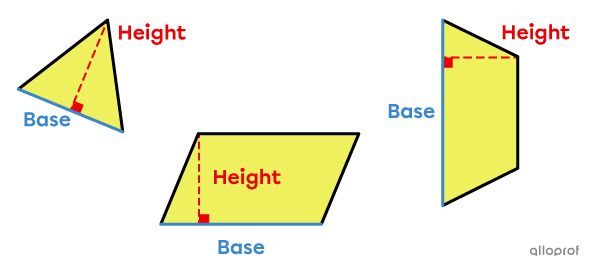
The height and base are always perpendicular. In other words, an angle of |90^\circ| is formed at the point of intersection of the 2 segments (or their extension).
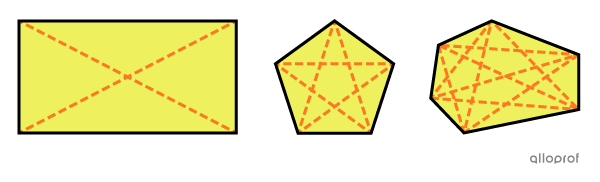
A diagonal is a segment connecting 2 non-consecutive vertices. Therefore, there is more than one diagonal in a single polygon.
A polygon is named according to its number of sides, regardless of its characteristics. Since there are an infinite number of different polygons, the following are the names of the most commonly used ones.
|
Number of Sides |
Polygon Name |
Examples |
|---|---|---|
|
3 |
Triangle |
 |
|
4 |
Quadrilateral |
 |
|
5 |
Pentagon |
 |
|
6 |
Hexagon |
 |
|
7 |
Heptagon |
 |
|
8 |
Octagon |
 |
|
9 |
Nonagon (enneagon) |
 |
|
10 |
Decagon |
 |
|
11 |
Hendecagon |
 |
|
12 |
Dodecagon |
 |
It is possible to define triangles and quadrilaterals according to the measurements of their angles, sides, or diagonals.
Convex polygons are distinguished from non-convex polygons by the measurements of their interior angles.
A polygon is convex if all its interior angles have a measure that is less than |180^\circ.|

All regular polygons are convex polygons.
A polygon is non-convex (concave) if it has at least one interior angle with a measure greater than |180^\circ.|

A polygon is regular if all its sides and interior angles have the same measurement.

A complex polygon is a polygon with at least 2 intersecting sides.

To understand the complex polygon, we must remember the definition of a polygon: it is a figure formed by a closed broken line.
To properly define each polygon, their properties are established according to the following concepts.
Some polygons have one or more axes of symmetry.
An axis of symmetry is a line that cuts a figure into 2 identical parts.
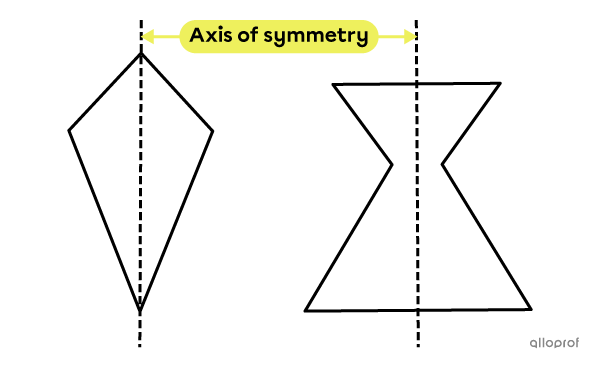
If you fold a polygon in half along the axis of symmetry, the 2 parts would match perfectly.
A polygon can be identified by the measurements of its sides and angles, but also by the position of their relationship to each other.
A pair of adjacent (consecutive) sides of a polygon consists of 2 sides with a common vertex.
There are as many pairs of consecutive sides as vertices in a polygon.
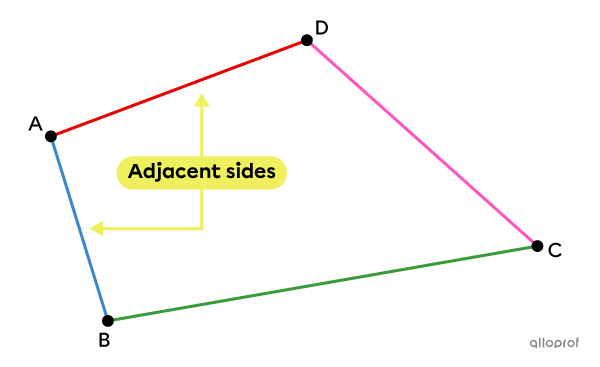
In this case, the pairs of adjacent sides are the following:
-
|\color{#ec0000}{\overline{AD}}| and |\color{#3b87cd}{\overline{AB}};|
-
|\color{#ec0000}{\overline{AD}}| and |\color{#ff55c3}{\overline{CD}};|
-
|\color{#3a9a38}{\overline{BC}}| and |\color{#3b87cd}{\overline{AB}};|
-
|\color{#3a9a38}{\overline{BC}}| and |\color{#ff55c3}{\overline{CD}}.|
We can also compare the position of the polygon's angles.
Consecutive angles of a polygon are angles that share a common side in the polygon.
Therefore, we can determine there are as many pairs of consecutive angles as vertices in a polygon.
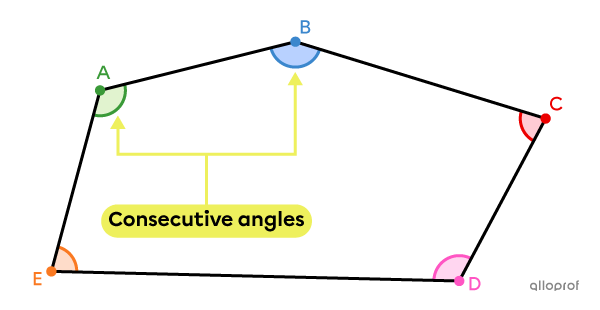
In the case of this polygon, the pairs of consecutive angles are the following:
-
|\color{#3a9a38}{\angle{A}}| and |\color{#3b87cd}{\angle{B}};|
-
|\color{#3b87cd}{\angle{B}}| and |\color{#ec0000}{\angle{C}};|
-
|\color{#ec0000}{\angle{C}}| and |\color{#ff55c3}{\angle{D}};|
-
|\color{#ff55c3}{\angle{D}}| and |\color{#fa7921}{\angle{E}};|
-
|\color{#fa7921}{\angle{E}}| and |\color{#3a9a38}{\angle{A}}.|
Based on the number of sides of a polygon, the relative position between 2 angles, 2 sides, or an angle and a side can be established.
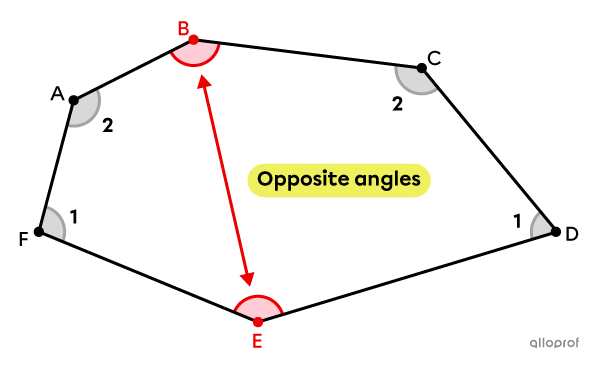
In this hexagon, the pairs of opposite angles (vertices) are the following:
-
|\color{#EC0000}B| and |\color{#EC0000}E;|
-
|C| and |F;|
-
|A| and |D.|
Note: Each pair of opposite angles are separated by the same number of vertices (2 in the case of the hexagon), no matter on which side they are counted.

This hexagon has the following pairs of opposite sides:
-
|\color{#3b87cd}{\overline{AF}}| and |\color{#3b87cd}{\overline{CD}};|
-
|\overline{AB}| and |\overline{DE};|
-
|\overline{BC}| and |\overline{EF}.|
Note: The pair of opposite sides is separated by the same number of line segments (2 in the case of the hexagon), no matter what side we choose.
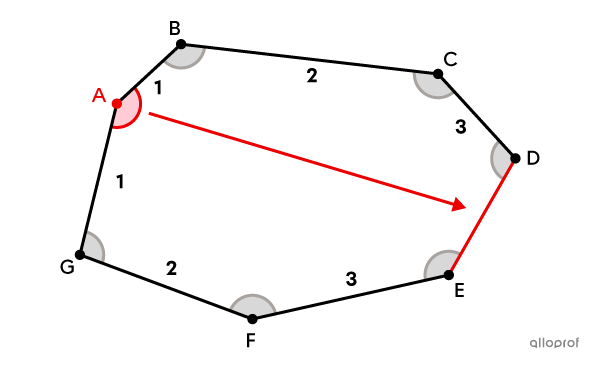
Angle (vertex) |\color{#ec0000}{A}| and side |\color{#ec0000}{\overline{DE}}| are opposite. They are separated by |3| sides.
The 2 following formulas calculate the sum of the interior angles of a polygon according to the number of sides. They are equivalent.
|\begin{align}\text{Sum}\ \text{int.}\angle \ &=(n-2) \times 180\\\\ \text{Sum}\ \text{int.} \angle \ &=180n-360\end{align}|
where
|n:| number of sides of the polygon
|
Polygon |
|\boldsymbol{\textbf{Sum}\ \ \textbf{int.}\angle= (n-2) \times 180}| |
|---|---|
|
Triangle |
|\text{Sum}\ \text{int.}\angle = (3-2) \times 180=180^\circ| |
|
Quadrilateral |
|\text{Sum}\ \text{int.}\angle = (4-2) \times 180=360^\circ| |
|
Pentagon |
|\text{Sum}\ \text{int.}\angle = (5-2) \times 180=540^\circ| |
|
Hexagon |
|\text{Sum}\ \text{int.}\angle = (6-2) \times 180=720^\circ| |
|
Heptagon |
|\text{Sum}\ \text{int.}\angle = (7-2) \times 180=900^\circ| |
|
Octagon |
|\text{Sum}\ \text{int.}\angle = (8-2) \times 180=1\ 080^\circ| |
|
Nonagon (Enneagon) |
|\text{Sum}\ \text{int.}\angle = (9-2) \times 180=1\ 260^\circ| |
|
Decagon |
|\text{Sum}\ \text{int.}\angle = (10-2) \times 180=1\ 440^\circ| |
|
Hendecagon |
|\text{Sum}\ \text{int.}\angle = (11-2) \times 180=1\ 620^\circ| |
|
Dodecagon |
|\text{Sum}\ \text{int.}\angle = (12-2) \times 180=1\ 800^\circ| |
