Free fall is the vertical movement that occurs when an object is subject only to the effect of gravitational force.
If we neglect the friction of air, an object in free-fall always experiences an acceleration of |\small 9,8 \: \text {m/s}^{2}| towards the ground.
|g = -9.8 \: \text {m/s}^{2}|
This means that if we drop a pea and a bowling ball from the top of the same building, both objects will accelerate at the same rate and arrive at the bottom of the building at the same time (that is if we neglect friction, which will slow the fall of any object).
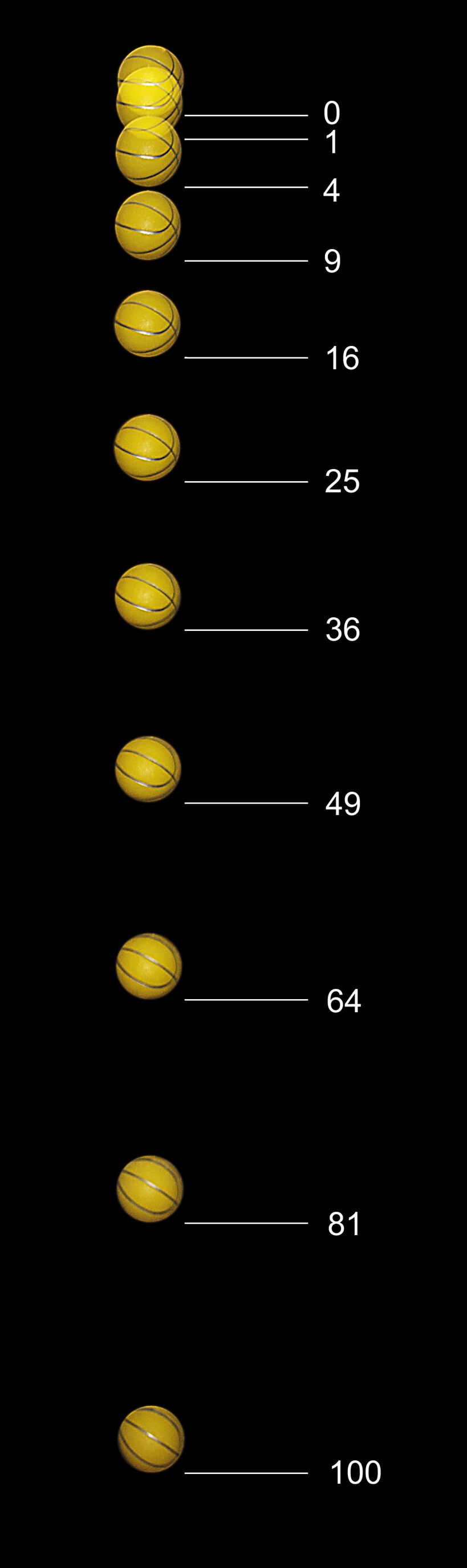
When a basketball is dropped towards the ground, every second it travels a greater distance because it is subjected to a gravitational force. Its acceleration is equal to the Earth's gravitational acceleration.
Earth's gravitational acceleration is not the same as the gravitational acceleration of other celestial bodies in the solar system. The magnitude of the acceleration depends, among other things, on the mass of the celestial body. The Moon, which is 81 times smaller than Earth, has a gravitational acceleration that is six times smaller than that of Earth, that is |{g} = 1.6 \: \text {m/s}^{2}.|
Since we're talking about accelerated rectilinear motion, the UARM equations apply in the case of free fall. Remember, however, that the acceleration of a falling object is always equal to the gravitational acceleration.
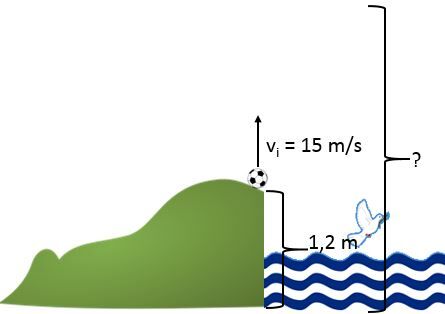
A ball is tossed upwards at a speed of |15.0\ \text {m/s}.| The ball is launched from a height of |1.2\ \text{m}| above the ground. What will be the maximum height reached by the ball?
In this type of problem, remember that when the ball reaches its maximum height, the speed is always equal to
\begin{align}a &= g = -9.8 \: \text{m/s}^2, & x_{i} &= 1.2 \: \text{m}, \\v_{i} &= 15.0 \: \text{m/s}, & v_{f} &= 0 \: \text{m/s}, \\x_{f} &= \: ?\end{align}
Using one of the UARM equations, it's possible to find the final position of the ball.
\begin{align}{v_{f}}^2 &= {v_{i}}^2 + 2 \cdot a \cdot \triangle x \quad \Rightarrow \quad \triangle x = \frac{{v_{f}}^2 - {v_{i}}^2}{2 \cdot a} \\&= \frac{(0 \: \text{m/s})^2 - (15 \: \text{m/s})^2}{2 \cdot (-9.8 \: \text{m/s}^2)} \\&= \frac{-225}{-19.6} \\&= 11.5 \: \text{m}\end{align} \begin{align} \triangle x = x_f - x_i \quad \Rightarrow \quad x_f &= \triangle x + x_i \\ &= 11.5 \: \text {m} + 1.2 \: \text {m} \\ &=12.7 \: \text {m} \end{align}
When an object is thrown upwards vertically, it will rise until it reaches its maximum height. The object then falls to the ground like a body in freefall. To simplify the solution, we need to separate the problem into two parts.
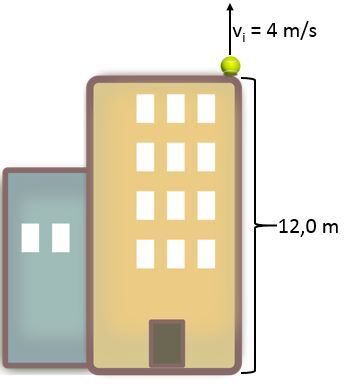
A ball is thrown upwards from the roof of a building measuring |120 \: \text {m}|, at a speed of |4.0 \: \text {m/s}.| How long will it take for the ball to reach the ground?
First, consider the upward movement the ball will make.
||\begin{align}a &= g = -9.8 \:\text{m/s}^2 &x_{i} &= 12 \: \text{m} \\ v_i &= 4.0 \:\text{m/s} &v_{f} &= 0 \: \text{m/s}\\
\triangle t &= ? \end{align}||
Using the UARM equations, we can find the time required for the ball to reach the highest point..
||\begin{align} {v_{f}}={v_{i}}+ a \cdot \triangle t
\quad \Rightarrow \quad
\triangle t &=\frac {{v_{f}} -{v_{i}}}{a} \\
&= \frac {{0 \: \text {m/s}} -{4 \: \text {m/s}}}{-9.8 \: \text {m/s}^2}\\
&= 0.41 \: \text{s} \end{align}||
The next step is to determine the maximum height reached by the ball.
||\begin{align} {v_{f}}^2={v_{i}}^2+2 \cdot a \cdot \triangle x
\quad \Rightarrow \quad
\triangle x &=\frac {{v_{f}}^2 -{v_{i}}^2}{2 \cdot a} \\
&= \frac {{(0 \: \text {m/s})}^2 -{(4 \: \text {m/s})}^2}{2 \cdot -9.8 \: \text {m/s}^2}\\
&= 0.8 \: \text{m} \end{align}||
||\begin{align} \triangle x = x_f - x_i
\quad \Rightarrow \quad
x_f &= \triangle x + x_i \\
&= 12 \: \text {m} + 0.8 \: \text {m}\\
&= 12.8 \: \text{m} \end{align}||
For the second part, consider that the object is in free fall from its highest point until it reaches the ground.
||\begin{align}a &= g = -9.8 \:\text{m/s}^2 &\triangle x &= -12.8 \: \text{m} \\ v_i &= 0 \:\text{m/s}
&\triangle t &= ? \end{align}||
Using one of the UARM equations, we can find the time required for the object to reach the ground.
||\begin{align} \triangle x= v_{i} \cdot \triangle t + \frac{1}{2} \cdot a \cdot {\triangle t}^{2}
\quad \Rightarrow \quad
\triangle x&= 0 \: \text {m/s} \cdot \triangle t + \frac{1}{2} \cdot a \cdot {\triangle t}^{2}\\
\triangle x&= \frac{1}{2} \cdot a \cdot {\triangle t}^{2}\\
\triangle t&= \sqrt{\frac {2 \cdot \triangle x}{a}} \\
&= \sqrt{\frac {2 \cdot -12.8 \: \text {m}}{-9.8 \: \text {m/s}^2}} \\
&= 1.62 \: \text{s} \end{align}||
Given that the upward movement lasted |0.41 \: \text{s}| and the downward movement had a duration of |1.62 \: \text{s}|, the time required for the ball to reach the ground is |0.41 \: \text{s}+1.62 \: \text{s}=2.03 \: \text{s}.|
For free-falling objects, it is also possible to derive graphical relationships from laboratory data.
Suppose an object is dropped from the top of a building, and the object's displacement as a function of time is examined.
Position of Free-Falling Object as a Function of Time
|
Time |(\text {s})| |
Position |(\text {m})| |
| |0| | |0| |
| |1| | |-4.9| |
| |2| | |-19.6| |
| |3| | |-44.1| |
| |4| | |-78.4| |
Graphically, the relationship obtained is a quadratic function oriented downwards, since gravitational acceleration is oriented in this direction. The curve obtained is of the same nature as that for an object following a URAM.
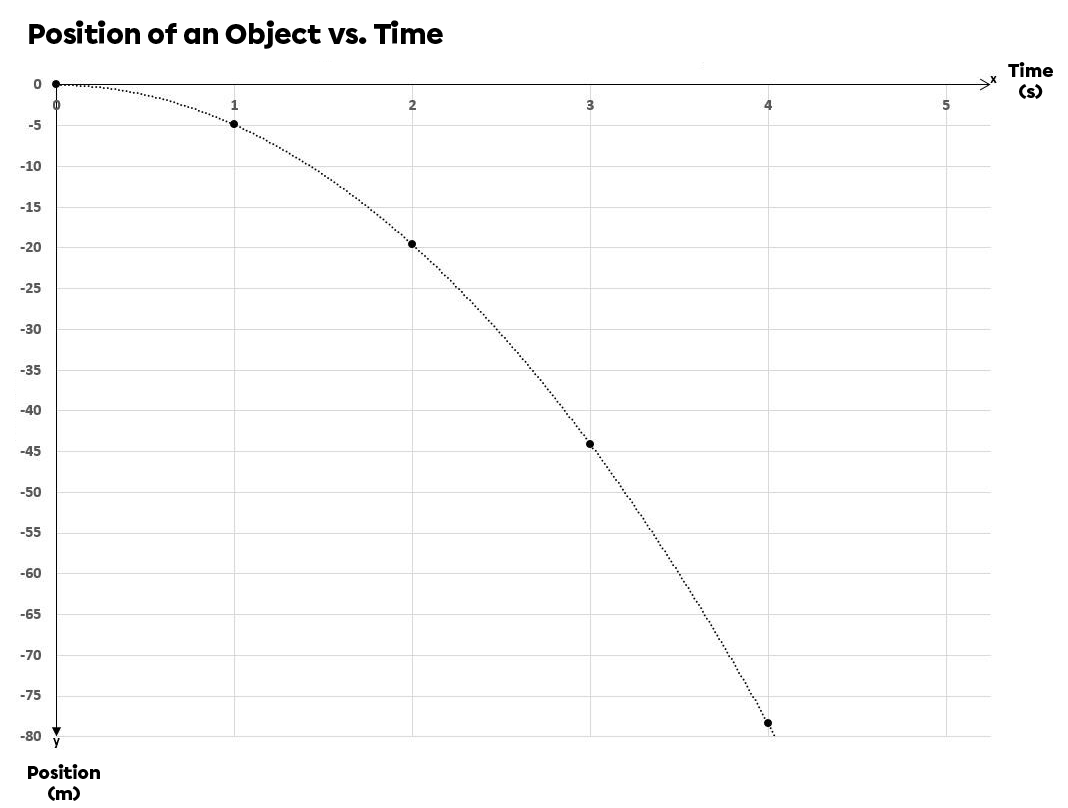
Every second the object covers a greater and greater distance. From this graph, we can determine the average speed by calculating the slope between two points. To calculate instantaneous speed, draw the tangent of the curve at the desired point, then calculate the slope of this tangent line.
It is also possible to start to study the motion at maximum height and record the position until the object reaches the ground. It is very important to establish the position of the reference system before graphing.
If we calculate the instantaneous speed for each of the positions measured during the object's free fall, we can determine the graphical relationship between the speed and time for this object.
Speed of a Falling Object as a Function of Time
|
Time |(\text {s})| |
Speed |(\text {m/s})| |
| |0| | |0| |
| |1| | |-9.8| |
| |2| | |-19.6| |
| |3| | |-29.4| |
| |4| | |-39.2| |
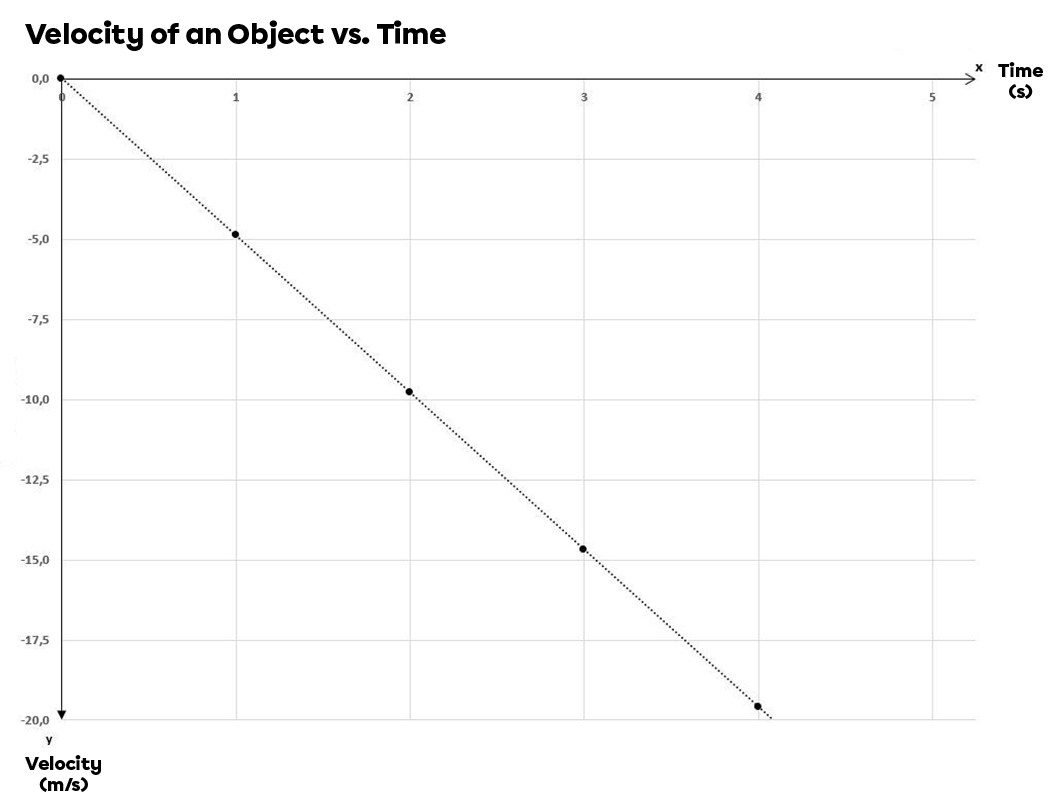
The resulting graph is a decreasing linear relationship. It's important to remember that the negative sign is only related to the direction of movement: a negative value indicates an object moving in the opposite direction to the reference system.
The graphical analysis shows us that the speed is increasing more and more negatively, at a rate of |9.8 \: \text {m/s}| every second. The linear relationship obtained is similar to that obtained for an UARM.
Lastly, the graph of acceleration versus time produces a null (constant) function, whose value is always equal to the value of gravitational acceleration, or |-9.8 \: \text {m/s}^2.| A negative value means that the object is moving downwards towards the ground.
Acceleration of a Free-Falling Object as a Function of Time
|
Time |(\text {s})| |
Acceleration |(\text {m/s}^2)| |
| |0| | |-9.8| |
| |1| | |-9.8| |
| |2| | |-9.8| |
| |3| | |-9.8| |
| |4| | |-9.8| |