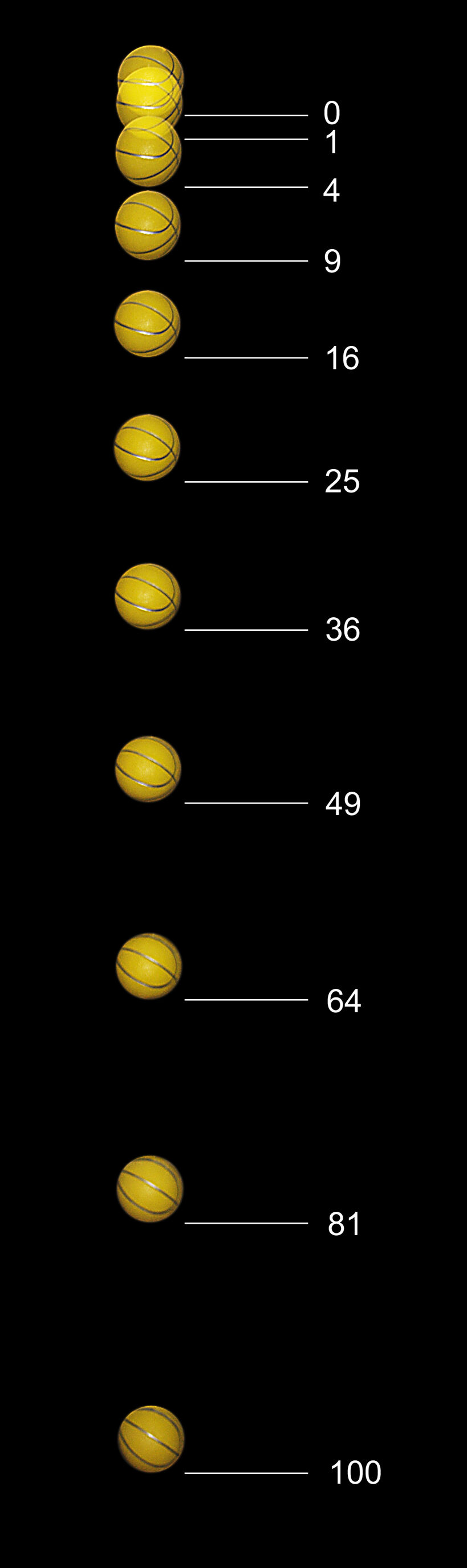
La chute libre est le mouvement vertical effectué par un objet lorsqu'il ne subit que l'effet de la force gravitationnelle.
Si on néglige le frottement de l'air, un objet qui effectue un mouvement de chute libre subit toujours une accélération de |\small 9,8 \: \text {m/s}^{2}| orientée vers le sol.
|g = -9,8 \: \text {m/s}^{2}|
Ceci signifie que si on laisse tomber un petit pois et une boule de quilles du sommet du même immeuble, les deux objets accéléreront au même taux et arriveront en bas de l’édifice en même temps (si on néglige le frottement, qui ralentira la chute de tout objet).
Lorsqu'un ballon de basketball est lancé vers le sol, le ballon parcourt une distance de plus en plus grande chaque seconde, car il subit une force gravitationnelle. Son accélération est égale à l'accélération gravitationnelle terrestre.
L'accélération gravitationnelle terrestre est différente de l'accélération gravitationnelle sur les autres astres du système solaire. La grandeur de l'accélération dépend, entre autres, de la masse de l'astre. La Lune, qui est |\small 81| fois plus petite que la Terre, a une accélération gravitationnelle six fois plus petite que sur la Terre, soit |\small {g} = 1,6 \: \text {m/s}^{2}|.
Puisqu'il s'agit d'un mouvement rectiligne accéléré, les équations du MRUA s'appliquent dans le cas d'une chute libre. Il faut toutefois se rappeler que l'accélération de l'objet en chute libre est toujours égale à celle de l'accélération gravitationnelle.
On lance une balle vers le haut avec une vitesse de |15{,}0\ \text {m/s}|. La balle est lancée à partir d'une hauteur de |1{,}2\ \text{m}| par rapport au sol. Quelle sera la hauteur maximale atteinte par la balle?
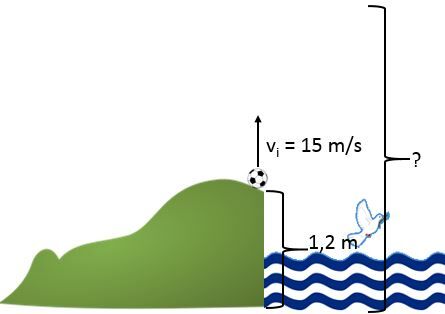
Dans ce type de problème, il faut se rappeler que lorsque la balle atteint sa hauteur maximale, la vitesse est toujours égale à |\small 0 \: \text {m/s}|.
||\begin{align}
a = g &= -9,8 \: \text {m/s}^2 &x_{i} &= 1,2 \: \text {m} \\
v_{i} &= 15,0 \: \text {m/s} &v_{f} &= 0 \: \text {m/s} \\
x_{f} &= \: ?
\end{align}||
En utilisant l'une des équations du MRUA, il est possible de déterminer la position finale de la balle.
||\begin{align} {v_{f}}^2 = {v_{i}}^2 + 2 \cdot a \cdot \triangle x
\quad \Rightarrow \quad
\triangle x &= \frac{{v_{f}}^2 - {v_{i}}^2}{2 \cdot a} \\
&= \frac{(0 \: \text {m/s})^2 - (15 \: \text {m/s})^2 }{2 \cdot (-9,8 \: \text {m/s}^{2})}\\
&= \frac{-225 }{-19,6}\\
&= 11,5 \: \text {m} \end{align}|| ||\begin{align} \triangle x = x_f - x_i \quad \Rightarrow \quad x_f &= \triangle x + x_i \\ &= 11,5 \: \text {m} + 1,2 \: \text {m} \\ &=12,7 \: \text {m} \end{align}||
Lorsqu'un objet est lancé verticalement vers le haut, il va monter jusqu'à atteindre sa hauteur maximale. Ensuite, l'objet atteindra le sol comme un corps en chute libre. Il faut donc séparer le problème en deux parties pour en simplifier sa résolution.
Du toit d'un édifice de |\small 12,0 \: \text {m}|, on lance vers le haut une balle avec une vitesse de |\small 4,0 \: \text {m/s}|. Combien de temps la balle prendra-t-elle pour atteindre le sol?
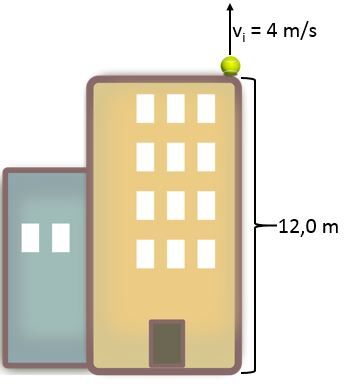
En premier lieu, il faut considérer le mouvement vers le haut que la balle va effectuer.
||\begin{align}a &= g = -9,8 \:\text{m/s}^2 &x_{i} &= 12 \: \text{m} \\ v_i &= 4,0 \:\text{m/s} &v_{f} &= 0 \: \text{m/s}\\
\triangle t &= ? \end{align}||
En utilisant les équations du MRUA, il est possible de trouver le temps nécessaire pour que la balle atteigne le point le plus haut.
||\begin{align} {v_{f}}={v_{i}}+ a \cdot \triangle t
\quad \Rightarrow \quad
\triangle t &=\frac {{v_{f}} -{v_{i}}}{a} \\
&= \frac {{0 \: \text {m/s}} -{4 \: \text {m/s}}}{-9,8 \: \text {m/s}^2}\\
&= 0,41 \: \text{s} \end{align}||
Il faut ensuite déterminer la hauteur maximale atteinte par la balle.
||\begin{align} {v_{f}}^2={v_{i}}^2+2 \cdot a \cdot \triangle x
\quad \Rightarrow \quad
\triangle x &=\frac {{v_{f}}^2 -{v_{i}}^2}{2 \cdot a} \\
&= \frac {{(0 \: \text {m/s})}^2 -{(4 \: \text {m/s})}^2}{2 \cdot -9,8 \: \text {m/s}^2}\\
&= 0,8 \: \text{m} \end{align}||
||\begin{align} \triangle x = x_f - x_i
\quad \Rightarrow \quad
x_f &= \triangle x + x_i \\
&= 12 \: \text {m} + 0,8 \: \text {m}\\
&= 12,8 \: \text{m} \end{align}||
Pour la deuxième partie, il faut considérer que l'objet est en chute libre à partir de son point le plus haut jusqu'à ce qu'il atteigne le sol.
||\begin{align}a &= g = -9,8 \:\text{m/s}^2 &\triangle x &= -12,8 \: \text{m} \\ v_i &= 0 \:\text{m/s}
&\triangle t &= ? \end{align}||
En utilisant l'une des équations du MRUA, on peut trouver le temps nécessaire pour que l'objet arrive au sol.
||\begin{align} \triangle x= v_{i} \cdot \triangle t + \frac{1}{2} \cdot a \cdot {\triangle t}^{2}
\quad \Rightarrow \quad
\triangle x&= 0 \: \text {m/s} \cdot \triangle t + \frac{1}{2} \cdot a \cdot {\triangle t}^{2}\\
\triangle x&= \frac{1}{2} \cdot a \cdot {\triangle t}^{2}\\
\triangle t&= \sqrt{\frac {2 \cdot \triangle x}{a}} \\
&= \sqrt{\frac {2 \cdot -12,8 \: \text {m}}{-9,8 \: \text {m/s}^2}} \\
&= 1,62 \: \text{s} \end{align}||
Considérant que le mouvement vers le haut fut d'une durée de |0,41 \: \text{s}| et que le mouvement vers le bas fut d'une durée de |1,62 \: \text{s}|, le temps nécessaire pour que la balle atteigne le sol est de |0,41 \: \text{s}+1,62 \: \text{s}=2,03 \: \text{s}|.
Dans le cas d'un objet en chute libre, il est également possible de déterminer des relations graphiques à partir des données obtenues en laboratoire.
Supposons qu'on laisse tomber un objet du haut d'un édifice et que le déplacement de l'objet en fonction du temps est déterminé.
Position de l'objet en chute libre en fonction du temps
| Temps |(\text {s})| | Position |(\text {m})| |
| |0| | |0| |
| |1| | |-4,9| |
| |2| | |-19,6| |
| |3| | |-44,1| |
| |4| | |-78,4| |
Graphiquement, la relation obtenue est une fonction quadratique orientée vers le bas, puisque l'accélération gravitationnelle est orientée dans ce sens. La courbe obtenue est de la même nature que celle tracée dans le cas d'un objet suivant un MRUA.
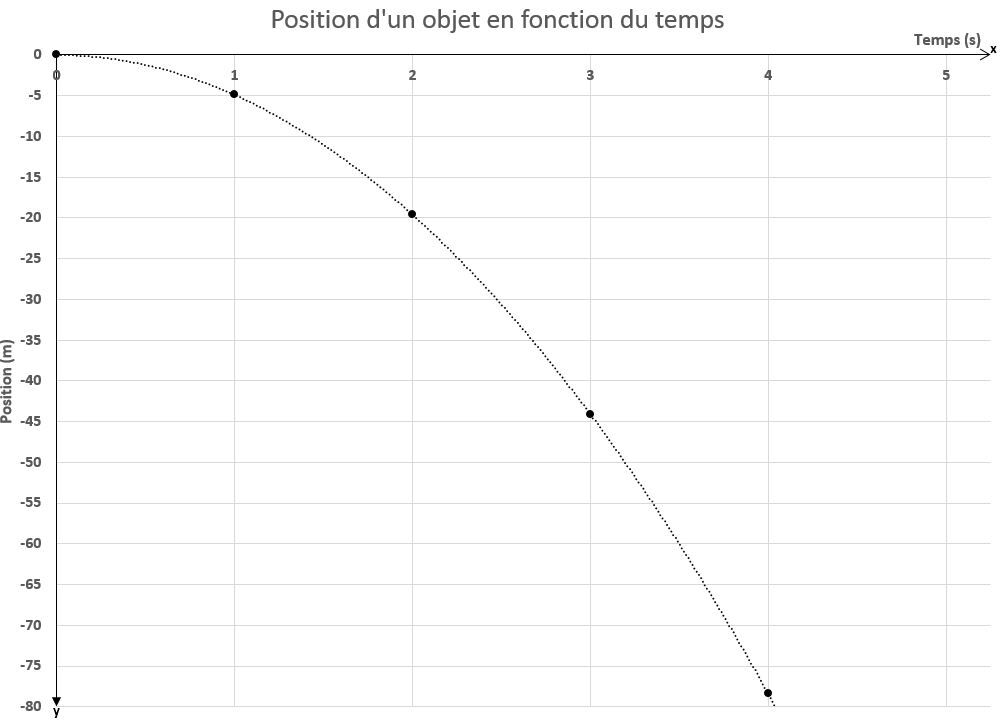
Ainsi, chaque seconde, l'objet parcourt une distance de plus en plus grande. À partir de ce graphique, il est possible de déterminer la vitesse moyenne en calculant la pente entre deux points. Pour calculer la vitesse instantanée, il faut dessiner la tangente de la courbe au point désiré, puis calculer la pente de cette tangente.
Il est également possible de commencer l'étude du mouvement à la hauteur maximale et de noter la position jusqu'à ce que l'objet atteigne le sol. Il est très important d'établir, avant de faire un graphique, quelle est la position du système de référence.
Si on calcule la vitesse instantanée pour chacune des positions mesurées lors de la chute libre de l'objet, on peut déterminer la relation graphique entre la vitesse et le temps pour cet objet.
Vitesse de l'objet en chute libre en fonction du temps
| Temps |(\text {s})| | Vitesse |(\text {m/s})| |
| |0| | |0| |
| |1| | |-9,8| |
| |2| | |-19,6| |
| |3| | |-29,4| |
| |4| | |-39,2| |
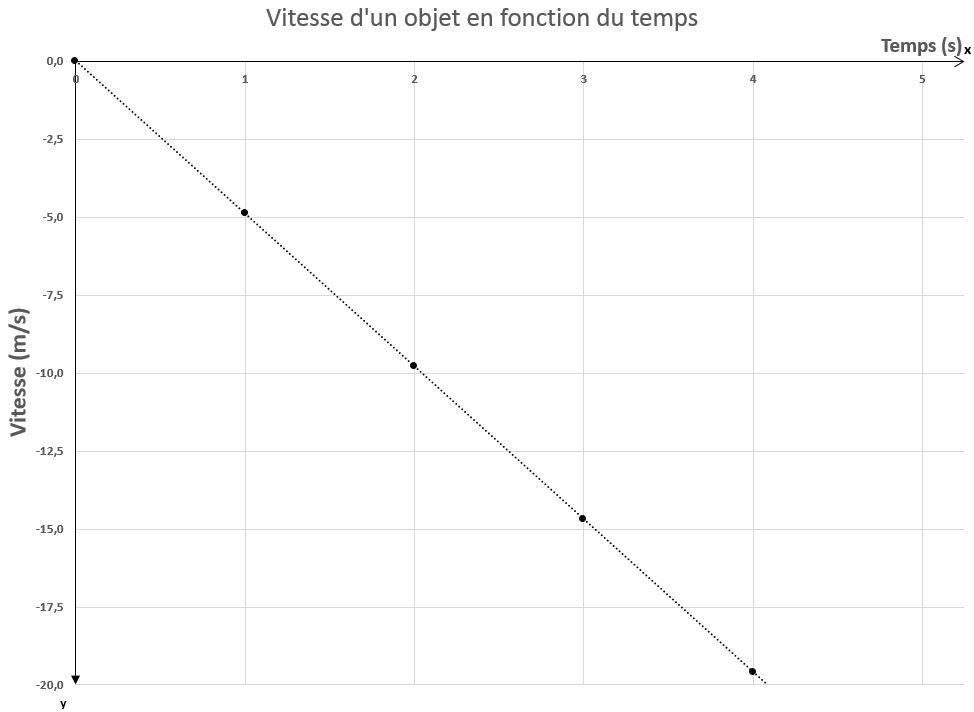
Le graphique obtenu est une relation linéaire décroissante. Il est important de rappeler que le signe négatif est uniquement relié au sens du mouvement: une valeur négative indique un objet se déplaçant dans le sens contraire au système de référence.
L'analyse graphique nous démontre que la vitesse augmente de plus en plus négativement, à un rythme de |9,8 \: \text {m/s}| à chaque seconde. La relation linéaire obtenue est semblable à celle tracée dans un MRUA.
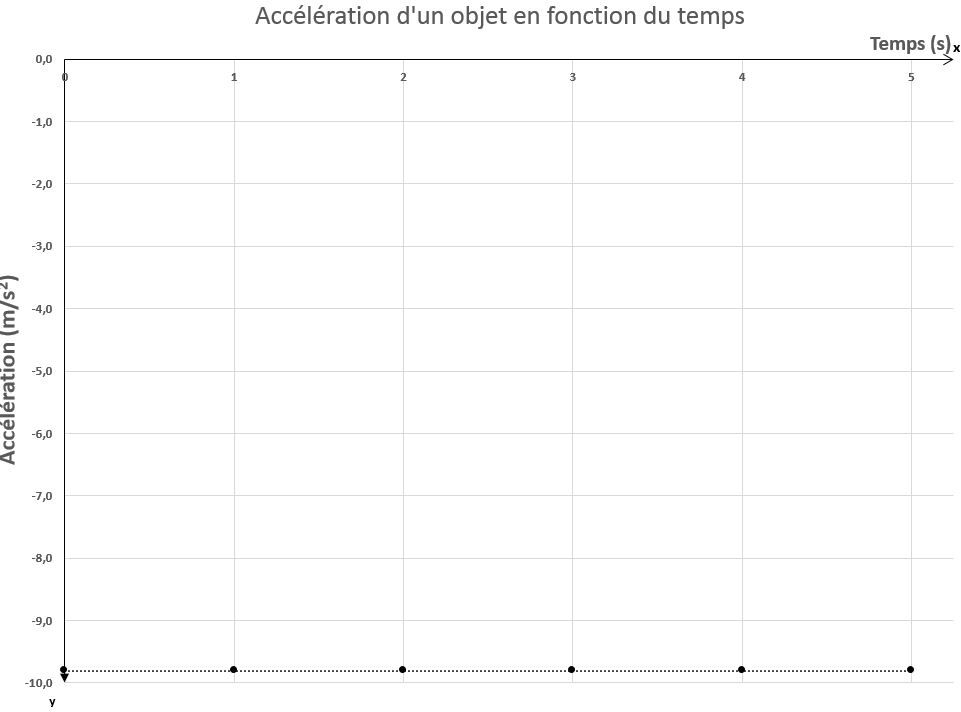
Finalement, le graphique d'accélération en fonction du temps permet d'obtenir une fonction nulle, dont la valeur est toujours égale à la valeur de l'accélération gravitationnelle, soit |-9,8 \: \text {m/s}^2|. La valeur négative signifie que l'objet se dirige vers le sol.
Accélération de l'objet en chute libre en fonction du temps
| Temps |(\text {s})| | Accélération |(\text {m/s}^2)| |
| |0| | |-9,8| |
| |1| | |-9,8| |
| |2| | |-9,8| |
| |3| | |-9,8| |
| |4| | |-9,8| |