When identifying a value of current intensity, voltage, or resistance in an electrical circuit, it is first necessary to identify the type of circuit (in series or in parallel) to determine which laws can be used to solve the problem. Kirchhoff's laws and the equivalent resistance formulas can be used to draw relationships according to the type of circuit. In addition, Ohm's law also permits making links between the three parameters studied in an electrical circuit.
Formulas to be used in electrical circuits
| Series circuit |
Parallel circuit
|
|
| Voltage |\left(\text{V}\right)| | |V_{t} \space \text {or} \space V_{s} = V_{1} + V_{2} + V_{3} + ...| | |V_{t} \space \text {or} \space V_{s} = V_{1} = V_{2} = V_{3} = ...| |
| Current intensity |\left(\text{A}\right)| | |I_{t} \space \text {or} \space I_{s} = I_{1} = I_{2} = I_{3} = ...| | |I_{t} \space \text {or} \space I_{s} = I_{1} + I_{2} + I_{3} + ...| |
|
Resistance|\left(\Omega\right)|
|
|R_{eq} = R_{1} + R_{2} + R_{3} + ...| | |\displaystyle \frac {1}{R_{eq}} = \frac {1}{R_{1}} + \frac {1}{R_{2}} + \frac {1}{R_{3}} + ...| |
What is the resistance of the resistor |R_{2}| ?
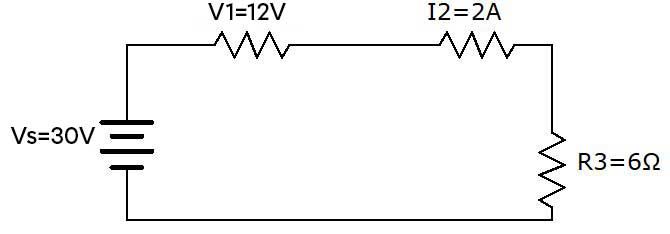
It is preferable to create a table in order to clearly identify the data known in the problem.
| Voltage | Resistance | Current Intensity |
|---|---|---|
| |V_{s} = 30 \text { V}| | |R_{eq} = | | |I_{s} = | |
| |V_{1} = 12 \text { V}| | |R_{1} = | | |I_{1} = | |
| |V_{2} = | | |R_{2} = | | |I_{2} = 2 \text{ A}| |
| |V_{3} = | | |R_{3}=6 \: \Omega| | |I_{3} =| |
Since this circuit is in series, the junction rule makes it possible to deduce that the intensity of the current will remain constant.
| Voltage | Resistance | Current Intensity |
|---|---|---|
| |V_{s} = 30 \: \text {V}| | |R_{eq} = | | |I_{s} = \color{red}{2 \: \text{A}}| |
| |V_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = \color{red}{2 \: \text{A}}| |
| |V_{2} = | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |V_{3} = | | |R_{3}=6 \: \Omega| | |I_{3} = \color{red}{2 \: \text{A}}| |
By using Ohm's Law, it is possible to determine the intensity of the current flowing through the third resistor.
||\begin{align} V_{3}= R_{3} \times I_{3} \quad \Rightarrow \quad V_{3}&= 6\ \Omega \times 2\ \text{ A} \\ &= 12 \text{ V} \end{align} ||| Voltage | Resistance | Current Intensity |
|---|---|---|
| |V_{s} = 30 \: \text {V}| | |R_{eq} = | | |I_{s} = 2 \: \text{A}| |
| |V_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = 2 \: \text{A}| |
| |V_{2} = | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |V_{3} = \color{red}{12 \: \text {V}} | | |R_{3}=6 \: \Omega| | |I_{3} = 2 \: \text{A}| |
Kirchhoff’s loop rule then makes it possible to deduce the intensity of the current flowing into the second resistor.
||\begin{align} V_{s}= V_{1} + V_{2} + V_{3} \quad \Rightarrow \quad V_{2}&= V_{s}- V_{1} - V_{3} \\ &= 30 \text{ V} - 12 \text{ V} - 12 \text{ V} \\ &= 6 \: \text {V}\end{align}||| Voltage | Resistance | Current Intensity |
|---|---|---|
| |V_{s} = 30 \: \text {V}| | |R_{eq} = | | |I_{s} = 2 \: \text{A}| |
| |V_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = 2 \: \text{A}| |
| |V_{2} = \color{red}{6 \: \text {V}} | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |V_{3} = 12 \: \text {V} | | |R_{3}=6 \: \Omega| | |I_{3} = 2 \: \text{A}| |
Finally, the resistance |R_{2}| can be calculated using Ohm's law.
||\begin{align} V_{2}= R_{2} \times I_{2} \quad \Rightarrow \quad R_{2}&= \frac{V_{2}}{I_{2}} \\ &= \frac{6 \text{ V}}{2 \text{ A}} \\ &= 3\ \Omega \end{align} || The resistor |R_2| has a resistance of |3\ \Omega| .
What is the equivalent resistance of this circuit?
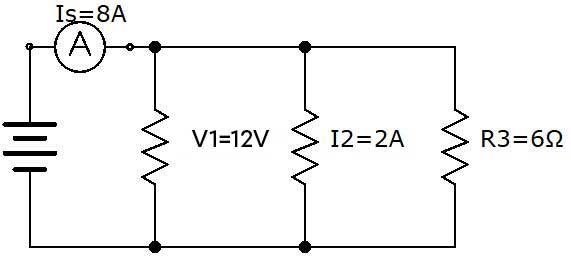
As in the previous example, it is preferable to create a table in order to clearly identify the data known in the problem.
| Voltage | Resistance | Current Intensity |
|---|---|---|
| |V_{s} = | | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |V_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = | |
| |V_{2} = | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |V_{3} = | | |R_{3}=6 \: \Omega| | |I_{3} =| |
Since the circuit is in parallel, Kirchhoff’s loop rule makes it possible to deduce that the voltage will always remain constant.
| Voltage | Resistance | Current Intensity |
|---|---|---|
| |V_{s} = \color{red}{12 \: \text {V}}| | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |V_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = | |
| |V_{2} =\color{red}{12 \: \text {V}} | | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |V_{3} =\color{red}{12 \: \text {V}} | | |R_{3}=6 \: \Omega| | |I_{3} =| |
Using Ohm's law, it is possible to determine the intensity of the current flowing through the third resistor.
||\begin{align} V_{3}= R_{3} \times I_{3} \quad \Rightarrow \quad I_{3}&= \frac{V_{3}}{R_{3}} \\ &= \frac{12 \text{ V}}{6 \ \Omega} \\ &= 2 \text{ A} \end{align}||| Voltage | Resistance | Current Intensity |
|---|---|---|
| |V_{s} = 12 \: \text {V}| | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |V_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = | |
| |V_{2} = 12 \: \text {V}| | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |V_{3} =12 \: \text {V}| | |R_{3}=6 \: \Omega| | |I_{3} =\color {red}{2 \: \text{A}}| |
The junction rule then makes it possible to deduce the intensity in the second resistor.
||\begin{align} I_{s} = I_{1} + I_{2} + I_{3} \quad \Rightarrow \quad I_{2}&= I_{s} - I_{1} - I_{3} \\ &= {8 \text{ A}}-{2 \ \text{ A} - 2\text{ A}} \\ &= 4 \text{ A} \end{align} ||| Voltage | Resistance | Current Intensity |
|---|---|---|
| |V_{s} = 12 \: \text {V}| | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |V_{1} = 12 \: \text {V}| | |R_{1} = | | |I_{1} = \color {red}{4 \: \text{A}}| |
| |V_{2} = 12 \: \text {V}| | |R_{2} = | | |I_{2} = 2 \: \text{A}| |
| |V_{3} =12 \: \text {V}| | |R_{3}=6 \: \Omega| | |I_{3} = 2 \: \text{A}| |
Resistance values of resistors |R_{1}| and |R_{2}| can be determined using Ohm's law. ||\begin{align} V_{1}= R_{1} \times I_{1} \quad \Rightarrow \quad R_{1}&= \frac{V_{1}}{I_{1}} & U_{2}= R_{2} \times I_{2} \quad \Rightarrow \quad R_{2}&= \frac{V_{2}}{I_{2}} \\ &= \frac{12 \text{ V}}{4 \text{ A}} &&= \frac{12 \text{ V}}{2 \text{ A}} \\ &= 3\ \Omega& &= 6\ \Omega \end{align} ||
| Voltage | Resistance | Current Intensity |
|---|---|---|
| |V_{s} = 12 \: \text {V}| | |R_{eq} = | | |I_{s} = 8 \: \text{A}| |
| |V_{1} = 12 \: \text {V}| | |R_{1} = \color {red}{3 \: \Omega}| | |I_{1} = 4 \: \text{A}| |
| |V_{2} = 12 \: \text {V}| | |R_{2} = \color {red}{6 \: \Omega}| | |I_{2} = 2 \: \text{A}| |
| |V_{3} =12 \: \text {V}| | |R_{3}=6 \: \Omega| | |I_{3} = 2 \: \text{A}| |
Finally, the equivalent resistance of the circuit can be calculated.
||\begin{align} \frac{1}{R_{eq}}= \frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}} \quad \Rightarrow \quad \frac{1}{R_{eq}} &= \frac{1}{3 \: \Omega}+\frac{1}{6 \: \Omega}+\frac{1}{6 \: \Omega} \\ \frac{1}{R_{eq}} &= \frac{4}{6 \: \Omega} \\ R_{eq} &= 1.5 \:\Omega \end{align}||The same result can be achieved by using Ohm's law.
||\begin{align} V_{s}= R_{eq} \times I_{s} \quad \Rightarrow \quad R_{eq}&= \frac{V_{s}}{I_{s}} \\ &= \frac{12 \text{ V}}{8 \text{ A}} \\ &= 1.5\ \Omega \end{align} || The equivalent resistance of this circuit is |1.5\ \Omega| .
Pour valider ta compréhension à propos des calculs dans les circuits électriques de façon interactive, consulte la MiniRécup suivante :
