Stoichiometry is the study of the proportions in which substances interact during a chemical reaction.
-
Stoichiometric coefficients are numbers placed in front of the chemical formulas of substances in a chemical equation. They indicate the proportions in which the substances interact in a chemical reaction.
-
Stoichiometric calculations are calculations in which the relationship between the ratio of stoichiometric coefficients and the ratio of quantities (in moles or numbers of particles) is used to calculate the amounts of reactants and products involved in a chemical reaction.
The balanced chemical equation of a chemical reaction is used to determine the proportions in which the reactants and products interact.
In a balanced chemical equation, the ratio between the stoichiometric coefficients of two substances is proportional to the ratio of their respective quantities expressed in moles or in the number of particles involved in the reaction.
In the following chemical reaction, the ratio between the stoichiometric coefficients of substances |\text{A}| and |\text{C}| is proportional to the ratio of their quantities expressed in moles.
||\begin{align}\color{#3A9A38}{a}\text{A}\ +\ \color{#3A9A38}{b}{\text{B}}&\rightarrow \color{#3A9A38}{c}\text{C}\ +\ \color{#3A9A38}{d}\text{D}\\\color{#3A9A38}{\text{Ratio of coefficients}}&=\color{#FA7921}{\text{Ratio of quantities (mol)}}\\ \dfrac{\color{#3A9A38}{a}}{\color{#3A9A38}{c}}&=\dfrac {\color{#FA7921}{n_{\text{A}}}}{\color{#FA7921}{n_{C}}}\end{align}||
where
|\color{#FA7921}{n}\!:| Quantity in moles (mol)
|\text{A, B, C, D}\!:| Chemical formulas of reactants and products
|\color{#3A9A38}{a, b, c,d}\!:| Stoichiometric coefficients
The ratio between the stoichiometric coefficients is proportional to the ratio of the quantities, only when the quantities are expressed in the number of moles or in the number of particles.

The ratio between the stoichiometric coefficients is not proportional to the mass ratio.
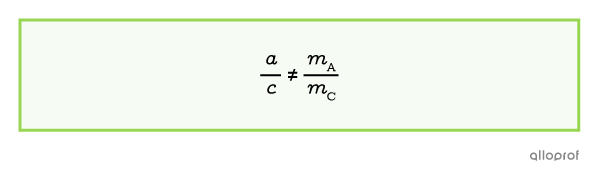
The ratio between two stoichiometric coefficients is also called molar ratio or stoichiometric ratio.
According to the following balanced chemical equation, how many moles of nitrogen |(\text{N}_2)| are produced as a result of the decomposition of |2.25\ \text{mol}| of ammonia |(\text{NH}_3)|?
||\color{#3A9A38}{2}\ \color{#FA7921}{\text{NH}_3}\rightarrow\ \color{#333FB1}{\text{N}_2}\ +\ \color{#3A9A38}{3}\ \color{#333FB1}{\text{H}_2}||
-
Identify the given data and missing value(s).
||\begin{align}n_{\text{NH}_3}&=2.25\ \text{mol}\\
n_{\text{N}_2}&=\ ?\ \text{mol}\end{align}|| -
Determine the proportion between the ratio of the stoichiometric coefficients and the ratio of the quantities.
In this reaction, the stoichiometric coefficients of ammonia |(\text{NH}_3)| and nitrogen |(\text{N}_2)| are |\color{#3A9A38}{2}| and |\color{#3A9A38}{1}| respectively. This means that the ratio between |\text{NH}_3| and |\text{N}_2| is 2 to 1. This ratio is proportional and therefore equal to the ratio of the respective quantities expressed in number of moles |(n).| ||\frac{\color{#3A9A38}{2}}{\color{#3A9A38}{1}}= \frac{n_{\text{NH}_3}}{n_{\text{N}_2}}|| -
Replace the variable with the known value.
||\frac{\color{#3A9A38}{2}}{\color{#3A9A38}{1}}= \frac{2.25\ \text{mol}}{n_{\text{N}_2}}|| -
Solve the equation. ||\begin{align}n_{\text{N}_2}&=\dfrac{\color{#3A9A38}{1}\times2.25}{\color{#3A9A38}{2}}\\ n_{\text{N}_2}&=1.13\ \text{mol}\end{align}||
When |2.25\ \text{mol}| of |\text{NH}_3| decomposes, |1.13\ \text{mol}| of |\text{N}_2| is produced.
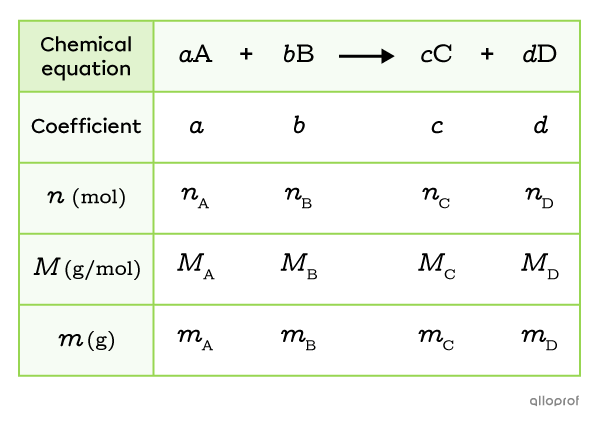
To facilitate the solution of a stoichiometry problem, a table can be used to organize the given data, the information sought and the calculated values. This method of working, sometimes called the table method, allows one to clearly visualize the stoichiometric calculations and to remember to make unit conversions when necessary.
This table generally includes five lines with the following information:
-
the balanced chemical equation
-
the stoichiometric coefficients
-
the number of moles |(n)|
-
the molar masses |(M)|
-
the masses |(m)|
Once the table is set up, the problem can be solved using the following steps.
-
Write the balanced chemical equation for the reaction and add the coefficients to the table.
-
Fill in the information provided in the problem.
-
Calculate and record the molar mass of each substance involved in the problem.
-
Convert the known reactant or product masses to moles.
-
Identify in the table the values to be calculated to solve the problem.
-
Calculate the number of moles of the desired reactant or product using a stoichiometric calculation.
-
Convert the number of moles to grams.
Depending on the problem, steps 3, 4 and 7 may not be necessary.
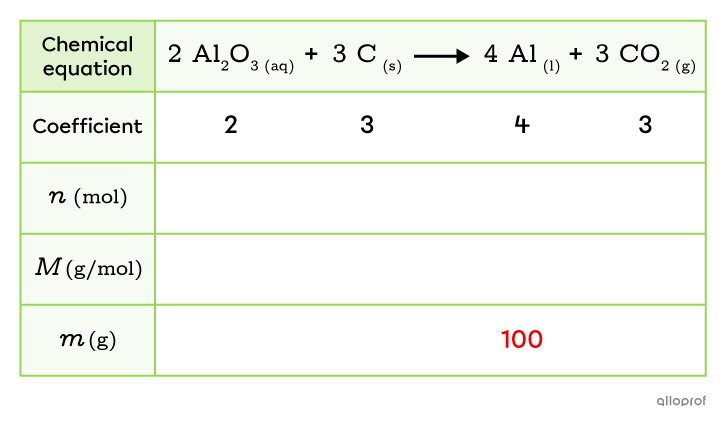
The electrolysis of an alumina solution |(\text{Al}_2\text{O}_{3})| produces aluminum |(\text{Al})| according to the following reaction.
||\text{Al}_2\text{O}_{3_{(aq)}}+\text{C}_{_{(s)}}\rightarrow\text{Al}_{_{(l)}}+\text{CO}_{2_{(g)}}||
What mass of carbon |(\text{C})| is required to produce |100 \text{g}| of aluminum |(\text{Al})|?
-
Write the balanced chemical equation for the reaction and add the coefficients to the table.

-
Fill in the information provided in the problem.
In this problem, the mass of aluminum |(\text{Al})| is |100\ \text{g}.|
-
Calculate and record the molar mass of the relevant substances.
In this problem, carbon |(\text{C})| and aluminum |(\text{Al})| are the relevant substances. Their molar masses are calculated and added to the table.

Attention: The calculation of the molar mass does not take into account the stoichiometric coefficients. -
Convert the known reactant or product masses to moles.
The number of moles of aluminum |(n_\text{Al})| that corresponds to the mass |(m_\text{Al})| of |100\ \text{g}| can be calculated using its molar mass |(M_\text{Al}).|
||\begin{align}M_{\text{Al}}=\dfrac{m_\text{Al}}{n_{\text{Al}}}\ \Rightarrow\ n_\text{Al}&=\dfrac{m_\text{Al}}{M_\text{Al}}\\\\
n_\text{Al}&=\dfrac{100\ \text{g}}{26.98\ \text{g/mol}}\\\\
n_\text{Al}&=3.71\ \text{mol}\end{align}||

-
Identify in the table the values to be calculated to solve the problem.
To solve the problem, the number of moles of carbon and its mass are required.
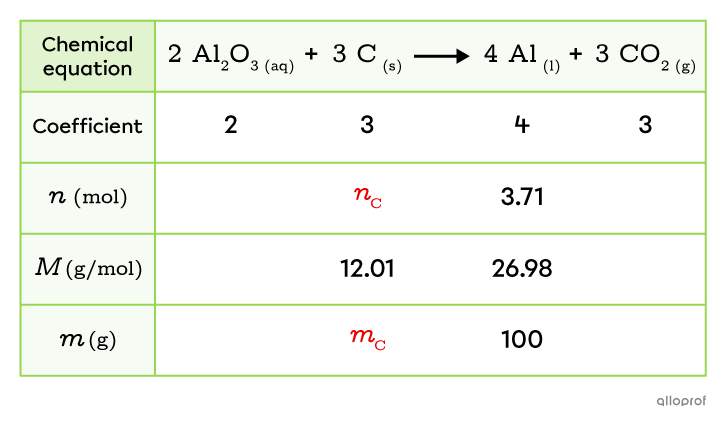
-
Calculate the number of moles of the desired reactant or product using a stoichiometric calculation.
The ratio of the stoichiometric coefficients is proportional to the ratio of the quantities expressed in moles. This relationship can be used to calculate the number of moles of carbon |(\text{C})| required to produce |3.71\ \text{mol}| of aluminum |(\text{Al}).|

||\begin{align}\dfrac{3}{4}&=\dfrac{n_{\text{C}}}{3.71\ \text{mol}}\\\\n_{\text{C}}&=\dfrac{3\times3.71\ \text{mol}}{4}\\\\
n_{\text{C}}&=2.78\ \text{mol}\end{align}||
-
Finally, convert the number of moles to grams.
The mass of |2.78\ \text{mol}| of carbon |(\text{C})| can be calculated using its molar mass.
||\begin{align}
M_{\text{C}}=\dfrac{m_\text{C}}{n_{\text{C}}}\ \Rightarrow\
m_{\text{C}}&={n_{\text{C}}}\times{M_\text{C}}\\m_{\text{C}}&={2.78\ \text{mol}}\times{12.01\ \text{g/mol}}\\m_{\text{C}}&=33.39\ \text{g}\end{align}||

A mass of |33.39\ \text{g}| of carbon is required to produce |100\ \text{g}| of aluminum in this reaction.
Pour valider ta compréhension à propos de la résolution d'un problème de stœchiométrie de façon interactive, consulte la MiniRécup suivante.
