-
Molar mass is the mass of one mole of a substance.
-
One mole corresponds to a group of |6.022\times10^{23}| particles.
The symbol for molar mass is |M| and its unit of measurement is the gram per mole |\text{(g/mol).}|
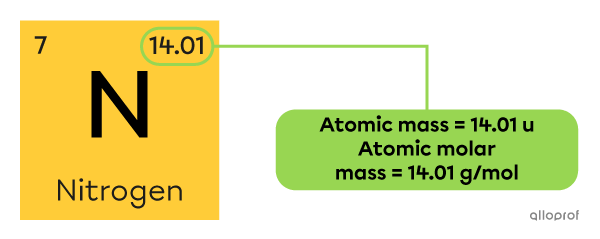
The molar mass of an element is also called the atomic molar mass, because it is the mass of one mole of atoms of that element.
The numerical value of the atomic molar mass of each element is found in the corresponding square of the periodic table. It is the same value as the atomic mass expressed in atomic units |\text{(u).}|
The atomic mass of nitrogen |\text{(N)}| is |14.01\ \text{u},| which means that its atomic molar mass is |14.01\ \text{g/mol.}| It can be written as follows:
||M_{\text{N}}=14.01\ \text{g/mol}||
In other words, one mole of nitrogen atoms has a mass of |14.01\ \text{g.}|
Or, a group of |6.022\times10^{23}| nitrogen atoms has a mass of |14.01\ \text{g.}|
To determine the molar mass of a substance made up of several atoms, the molar mass of all the atoms that make up the substance must be added together.
The different types of atoms and their quantities are indicated in the chemical formula of the substance.
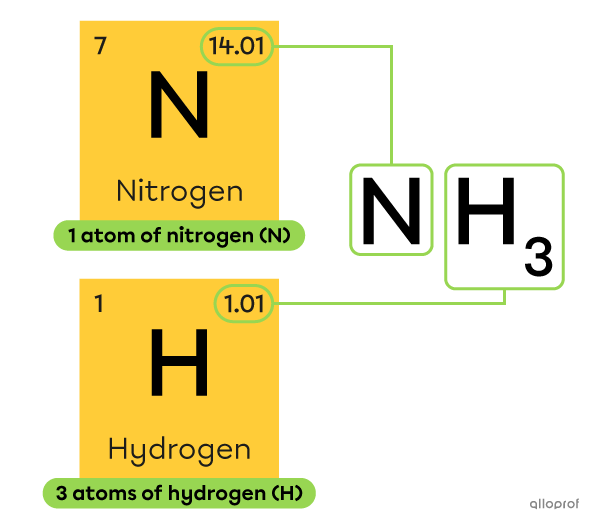
What is the molar mass of ammonia |\text{(NH}_3)|?
-
Let’s identify the given and missing data. The molar mass of nitrogen |\text{(N)}| and hydrogen |\text{(H)}| atoms that make up this substance can be determined using the periodic table.
||\begin{align} M_{\text{N}} &=14.01\ \text{g/mol}\\ M_{\text{H}} &=1.01\ \text{g/mol}\\ M_{\text{NH}_3} &=\ ?\ \text{g/mol}\end{align}|| -
The chemical formula of ammonia |\text{(NH}_3)| indicates that there is 1 nitrogen atom |\text{(N)}| and 3 hydrogen atoms |\text{(H).}| The molar mass of ammonia can be calculated as follows:
||M_{\text{NH}_3}=M_{\text{N}}+3\ M_{\text{H}}||
-
Let’s replace the variables with the known values and solve the problem.
||\begin{align}M_{\text{NH}_3} &=14.01\ \text{g/mol}+3\times1.01\ \text{g/mol}\\M_{\text{NH}_3} &=17.04\ \text{g/mol}\end{align}|| -
The final answer is:
The molar mass of ammonia is |17.04\ \text{g/mol.}|
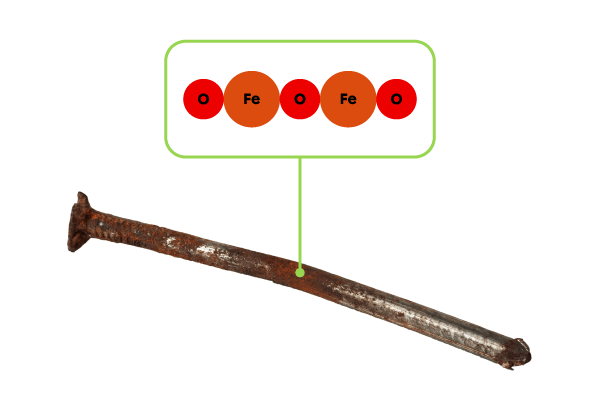
What is the molar mass of rust with a chemical formula |(\text{Fe}_2 \text{O}_3)|?
-
Let’s identify the given and missing data. The molar mass of iron |\text{(Fe)}| and oxygen |\text{(O)}| atoms that make up this substance can be determined using the periodic table.
||\begin{align}M_{\text{Fe}} &=55.85\ \text{g/mol}\\M_{ \text{O}} &=16.00\ \text{g/mol}\\M_{\text{Fe}_2 \text{O}_3} &=\ ?\ \text{g/mol}\end{align}|| -
The chemical formula of rust |(\text{Fe}_2 \text{O}_3)| indicates that there are 2 iron atoms |\text{(Fe)}| and 3 oxygen atoms |\text{(O)}.| The molar mass of rust can be calculated as follows: ||M_{\text{Fe}_2 \text{O}_3}=2\ M_{\text{Fe}}+3\ M_{\text{O}}||
-
Let’s replace the variables with the known values and solve the problem.
||\begin{align}M_{\text{Fe}_2 \text O_3} &=2\times55.85\ \text {g/mol}+3\times16.00\ \text{g/mol}\\M_{\text{Fe}_2 \text{O}_3} &=159.70\ \text{g/mol}\end{align}|| -
The final answer is:
The molar mass of rust is |159.70\ \text{g/mol.}|
What is the molar mass of aluminum sulfate |(\text{Al}_2(\text{SO}_4)_3)|?
-
Let’s identify the given and missing data. The molar mass of aluminum |\text{(Al)},| sulphur |\text{(S)}| and oxygen |\text{(O)}| atoms that make up this substance can be determined using the periodic table.
||\begin{align}M_{\text{Al}} &=26.98\ \text{g/mol}\\M_{ \text{S}} &=32.07\ \text{g/mol}\\M_{\text{O}} &=16.00\ \text{g/mol}\\M_{\text{Al}_2(\text {SO}_4)_3} &=\ ?\ \text{g/mol}\end{align}|| -
The chemical formula of aluminum sulphate |(\text{Al}_2(\text{SO}_4)_3)| indicates that there are 2 aluminum atoms |\text{(Al)},| 3 sulphur atoms |\text{(S)}| and 12 oxygen atoms |\text{(O).}| The molar mass of aluminum sulphate can be calculated as follows: ||M_{\text{Al}_2(\text{SO}_4)_3}=2\ M_{\text{Al}}\ +\ 3~M_{\text{S}}\ +~12\ M_{\text{O}}||
-
Let’s replace the variables with the known values and solve the problem.
||\begin{align}M_{\text{Al}_2(\text{SO}_4)_3} &=2\times26.98\ \text{g/mol}+3\times32.07\ \text{g/mol}+12\times16.00\ \text{g/mol}\\M_{\text{Al}_2(\text{SO}_4)_3} &=342.17\ \text{g/mol}\end{align}|| -
The final answer is:
The molar mass of aluminum sulphate is |342.17\ \text{g/mol.}|
The molar mass |(M)| of a substance corresponds to the mass |(m)| of that substance relative to its number of moles |(n).| The relationship between |M,| |n| and |m| can be expressed in three ways, depending on which variable needs to be isolated.
||M=\dfrac{m}{n}||
||m=nM||
||n=\dfrac{m}{M}||
where
|M\!:| molar mass in grams per mole |\text{(g/mol)}|
|m\!:| mass in grams |\text{(g)}|
|n\!:| number of moles in moles |\text{(mol)}|
The molar mass formula |M=\dfrac{m}{n}| explains why it is measured in |\text{g/mol.}|
The molar mass of calcium |\text{(Ca)}| corresponds to the mass of |40.08\ \text{g}| per |1\ \text{mol}.| By dividing |40.08\ \text{g}| by |1\ \text{mol},| the |\bf\text{g/mol}| unit is obtained for mole mass.
||M_{\text{Ca}}=\dfrac{m}{n}=\dfrac{40.08\ \bf\text{g}}{1\ \bf\text{mol}}=40.08\ \bf\text{g/mol}||
The |n=\dfrac{m}{M}| formula is used to calculate the number of moles of a substance based on its mass and its molar mass.
A salt shaker contains |97.02\ \text{g}| of sodium chloride |(\text{NaCl}),| commonly called table salt. How many moles of sodium chloride are in the salt shaker?

Source: Adapted from HandmadePictures, Shutterstock.com
-
Let's identify the given and missing values.
||\begin{align}n &=\ ?\ \text{mol}\\m &=97.02\ \text{g}\end{align}||The molar mass of sodium chloride |(\text{NaCl})| can be calculated as follows:
||\begin{align}\\M_{\text{NaCl}} &=M_{\text{Na}}+M_{\text{Cl}}\\M_{\text{NaCl}} &=22.99\ \text{g/mol}+35.45\ \text{g/mol}\\M_{\text{NaCl}} &=58.44\ \text{g/mol}\end{align}|| -
Since the number of moles |(n)| is unknown, the formula where it is isolated should be used.
||M=\dfrac{m}{n} \ \Rightarrow\ n=\dfrac{m}{M}|| -
Let’s replace the variables with the known values and solve the problem.
||\begin{align}n &=\dfrac{97.02\ \cancel{\text{g}}}{58.44\ \cancel{\text{g}}\text{/mol}}\\\\n &\approx1.660\ \text{mol}\end{align}|| -
The final answer is:
The salt shaker contains approximately |1.660\ \text{mol}| of sodium chloride.
The |m=nM| formula is used to calculate the mass of a substance based on the number of moles and its molar mass.
What is the mass of |2.25\ \text{mol}| of water |(\text{H}_2\text{O})|?
-
Let's identify the given and missing values.
||\begin{align}m &=\ ?\ \text{g}\\n &=2.25\ \text{mol}\end{align}||The molar mass of water |(\text{H}_2\text{O})| can be calculated as follows:
||\begin{align}\\M_{\text{H}_2\text{O}} &=2\ M_{\text{H}}+M_{\text{O}}\\M_{\text{H}_2\text{O}} &=2\times1.01\ \text{g/mol}+16.00\ \text{g/mol}\\M_{\text{H}_2\text{O}} &=18.02\ \text{g/mol}\end{align}|| -
Since the mass |(m)| is unknown, the formula where it is isolated should be used.
||M=\dfrac{m}{n} \ \Rightarrow\ m=nM|| -
Let’s replace the variables with the known values and solve the problem.
||\begin{align}m &=2.25\ \cancel{\text{mol}}\times18.02\ \text{g/}\cancel{\text{mol}}\\m &\approx40.5\ \text{g}\end{align}|| -
The final answer is:
The mass of |2.25\ \text{mol}| of water is approximately |40.5\ \text{g}.|
The amount of a substance is sometimes expressed as a number of particles |(\text{N}).| To calculate the mass of a substance (m) using its number of particles, the number of moles |(\text{n})| has to be determined first. Then, the mass can be calculated using the |m=nM| formula.
The following formula allows the calculation of the number of moles of a substance using its number of particles and Avogadro's number.
|n=\dfrac{N}{N_{\text{A}}}|
where
|n\!:| number of moles in moles |(\text{mol})|
|N\!:| number of particles |(\text{particules})|
|N_{\text{A}}\!:| Avogadro’s number |(6.022\times10^{23}\ \text{particules/mol})|
A sample contains |1.402\times10^{24}| atoms of carbon |(\text{C}).|
a) Determine the number of moles in the sample.
b) Determine the mass of the sample.
a) Determine the number of moles in the sample.
-
Let’s identify the given and missing values.
||\begin{align}n &=\ ?\ \text{mol}\\N &=1.402\times10^{24}\ \text{atoms}\\N_{\text{A}} &=6.022\times10^{23}\ \text{atoms/mol}\end{align}|| -
Choose the correct formula to use.
||n=\dfrac{N}{N_{\text{A}}}|| -
Let’s replace the variables with the known values and solve the problem:
||\begin{align}n &=\dfrac{1.402\times10^{24}\ {\cancel{\text{atoms}}}}{6.022\times10^{23}\ {\cancel{\text{atoms}}}\text{/mol}}\\\\n &\approx2.328\ \text{mol}\end{align}|| -
The answer is:
|1.402\times10^{24}| carbon atoms correspond to |2.328\ \text{mol}| of carbon.
b) Determine the mass of the sample.
-
Let’s identify the given and missing data. The molar mass of carbon |\text{(C)}| can be determined using the periodic table.
||\begin{align}m &=\ ?\ \text{g}\\n &=2.328\ \text{mol}\\M_{\text{C}} &=12.01\ \text{g/mol}\end{align}|| -
Since the mass |(m)| is unknown, the formula where it is isolated should be used.
||M=\dfrac{m}{n} \ \Rightarrow\ m=nM|| -
Let’s replace the variables with the known values and solve the problem:
||\begin{align}m &=2.328\ \cancel{\text{mol}}\times12.01\ \text{g/}\cancel{\text{mol}}\\m &\approx27.96\ \text{g}\end{align}|| -
The answer is:
|1.402\times10^{24}| carbon atoms correspond to approximately |27.96\ \text{g}| of carbon.
