L’addition et la soustraction sont des opérations qui se font avec des nombres positifs, mais aussi avec des nombres négatifs. Il faut donc s’assurer d’être à l’aise avec l’ensemble des nombres entiers. Il existe un lien étroit entre la soustraction et l’addition, puisque ce sont des opérations inverses l’une par rapport à l’autre.
Il existe plusieurs approches pour comprendre l’addition de nombres positifs et négatifs. La méthode des jetons et celle de la droite numérique sont des méthodes visuelles qui fonctionnent uniquement avec les nombres entiers.
La méthode des jetons permet de comprendre l’addition de nombres entiers à l’aide de manipulations. Pour effectuer cette méthode, il faut avoir des jetons de 2 couleurs différentes : une pour les nombres négatifs et une autre pour les nombres positifs. Un jeton positif s’annule avec un jeton négatif. Pour trouver le résultat de l’addition, on doit compter le nombre de jetons restants. La couleur des jetons restants indique le signe de la réponse.
Additionner 2 nombres de même signe
Le résultat de l’addition |-8+-6| peut être représenté à l’aide de jetons de la façon suivante.
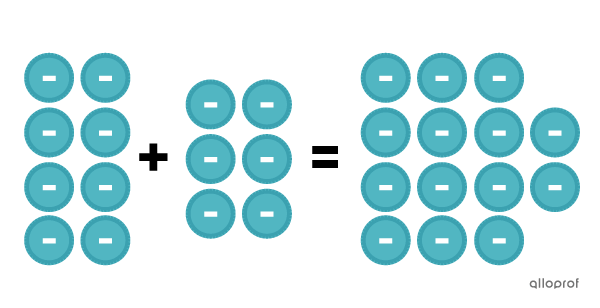
On ne peut pas annuler de jetons, puisqu’il n’y a pas 2 couleurs différentes. Alors, on additionne les jetons bleus ensemble, et on trouve qu’il y en a |14.| Étant donné qu’ils sont bleus, la couleur des jetons négatifs, on trouve que le résultat de l’addition |-8+-6| est |-14.|
Additionner 2 nombres de signes différents
Le résultat de l’addition |8+-6| peut être représenté à l’aide de jetons de la façon suivante.
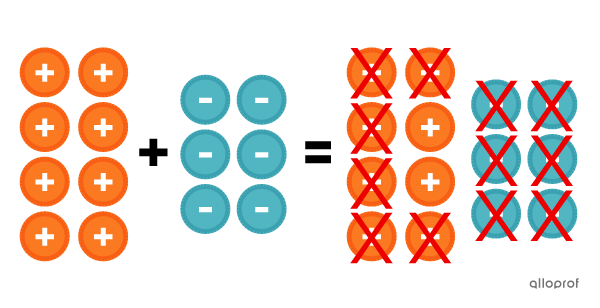
On annule chaque jeton bleu avec un jeton orange. Puisqu’il reste 2 jetons et qu’ils sont oranges, soit la couleur associée aux jetons positifs, on trouve que le résultat de l’addition |8+-6| est |+2,| ou |2,| tout simplement.
On peut utiliser la droite numérique pour effectuer l’addition de nombres entiers. Pour y arriver, on fait un point sur la droite là où se situe le 1er terme de l’addition. Le 2e terme indique le nombre de bonds à effectuer. S’il est positif, on fait les bonds vers la droite, et s’il est négatif, on fait les bonds vers la gauche. La somme est le nombre sur lequel on arrive après avoir fait tous les bonds.
Additionner 2 nombres de signes différents
Le résultat de l’addition |−4+8| peut être représentée à l’aide d’une droite numérique de la façon suivante.
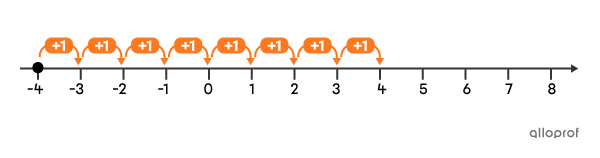
On commence par situer le 1er terme sur la droite numérique à l’aide d’un point à |-4.| Le 2e terme de l'addition est positif. Il nous indique qu'il faut faire |8| bonds vers la droite. On trouve que le résultat de l’addition |-4+8| est |4.|
Additionner 2 nombres de même signe
Le résultat de l’addition |-1+-4| peut être représenté à l’aide d’une droite numérique de la façon suivante.
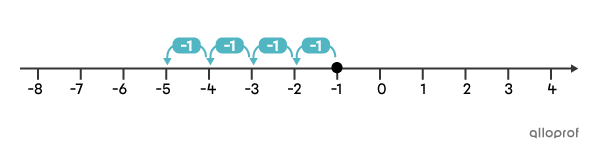
On commence par situer le 1er terme sur la droite numérique à l’aide d’un point à |-1.| Le 2e terme de l'addition est négatif. Il nous indique qu'il faut faire |4| bonds vers la gauche. On trouve que le résultat de l’addition |-1+-4| est |-5.|
En général, on utilise plutôt la méthode arithmétique, qui ne fonctionne pas uniquement pour les nombres entiers. En effet, elle permet également d'additionner des nombres décimaux ou d’additionner des fractions.
Cette méthode se base sur le sens des nombres. Ainsi, il faut associer un nombre positif à une quantité positive et un nombre négatif à une quantité négative. On utilise souvent les contextes d’argent |(\$)| ou de température |(^\circ \text{C})| pour bien comprendre ces concepts. On imagine qu'on part toujours de |0| (|0\ \$| dans un compte de banque ou de |0\ ^\circ \text{C}| sur un thermomètre). Un nombre positif représente donc un gain d’argent ou une augmentation de la température. Un nombre négatif représente quant à lui une perte d’argent ou une baisse de température.
Voici les différents cas qu’il est possible de retrouver.
|
Cas |
Démarche |
Exemple |
|---|---|---|
|
Les 2 nombres sont positifs. |
On additionne les 2 nombres. Le résultat est toujours positif. |
||\boldsymbol{\color{#fa7921}{65}} + \boldsymbol{\color{#fa7921}{17}}=\boldsymbol{\color{#fa7921}{82}}|| |
|
Les 2 nombres sont négatifs. |
On additionne les 2 nombres sans tenir compte des signes. Le résultat est toujours négatif. |
||\boldsymbol{\color{#51b6c2}{-24}} + \boldsymbol{\color{#51b6c2}{-18}}=\boldsymbol{\color{#51b6c2}{-42}}|| |
|
Les 2 nombres sont de signes contraires. |
On soustrait les 2 nombres sans tenir compte des signes. Le signe du résultat est le signe du terme qui est le plus éloigné de |0.| |
||\begin{alignat}{13}\boldsymbol{\color{#51b6c2}{-}}&\boldsymbol{\color{#51b6c2}{22}}&&+\phantom{-}&&\boldsymbol{\color{#fa7921}{8}}&&=\boldsymbol{\color{#51b6c2}{-}}&&\boldsymbol{\color{#51b6c2}{14}}\\&\boldsymbol{\color{#fa7921}{22}}&&+\boldsymbol{\color{#51b6c2}{-}}&&\boldsymbol{\color{#51b6c2}{8}}&&=&&\boldsymbol{\color{#fa7921}{14}}\end{alignat}|| |
Trouve le résultat de l’addition |6+3.|
Dans un contexte d’argent, l’addition |\boldsymbol{\color{#fa7921}{6}} + \boldsymbol{\color{#fa7921}{3}}| signifie qu’en partant de |0\ \$,| on a un gain de |\boldsymbol{\color{#fa7921}{6\ \$}}| suivi d’un gain de |\boldsymbol{\color{#fa7921}{3\ \$}}.| Finalement, on se retrouve avec encore plus d’argent.
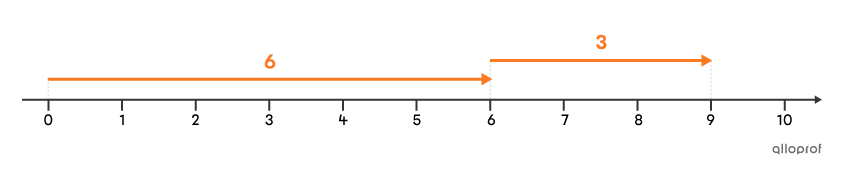
Pour trouver la somme, on fait l’addition |6+3,| et on trouve |\boldsymbol{\color{#fa7921}{9}}.| Comme les 2 termes sont positifs, la somme est également positive.
Réponse : Le résultat de l’addition |6+3| est |\boldsymbol{\color{#fa7921}{9}}.|
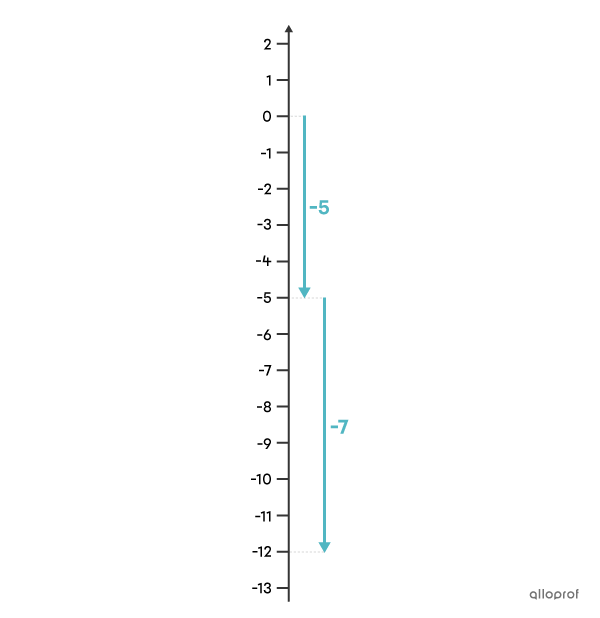
Trouve le résultat de l’addition |-5+-7.|
Dans un contexte de température, l’addition |\boldsymbol{\color{#51b6c2}{-5}}+\boldsymbol{\color{#51b6c2}{-7}}| signifie qu’en partant de |0\ ^\circ \text{C},| on a une baisse de température de |\boldsymbol{\color{#51b6c2}{5\ ^\circ \text{C}}},| à laquelle s’ajoute une autre baisse de |\boldsymbol{\color{#51b6c2}{7\ ^\circ \text{C}}}.| En résumé, la température finale est encore plus froide que celle mesurée au départ.
Pour trouver la somme, on fait l’addition des termes sans tenir compte des signes. |5+7| donne |12.| Comme les 2 termes sont négatifs, la somme est également négative.
Réponse : Le résultat de l’addition |-5+-7| est |\boldsymbol{\color{#51b6c2}{-12}}.|
Trouve le résultat de l’addition |6+-3.|
Dans un contexte de température, l’addition |\boldsymbol{\color{#fa7921}{6}} + \boldsymbol{\color{#51b6c2}{-3}}| signifie qu’en partant de |0\ ^\circ \text{C},| il y a une hausse de température de |\boldsymbol{\color{#fa7921}{6\ ^\circ \text{C}}}| suivie d’une baisse de |\boldsymbol{\color{#51b6c2}{3\ ^\circ \text{C}}}.| Comme la hausse de température est plus importante que la baisse, on se retrouve avec une température finale supérieure à |0\ ^\circ \text{C}.|
Les 2 termes sont de signes contraires. On fait donc la soustraction |6-3,| et on obtient |3.| Sur la droite, |6| est le nombre le plus éloigné de |0| (sa flèche est la plus longue). La réponse finale est donc positive.
Réponse : Le résultat de l’addition |6+-3| est |\boldsymbol{\color{#fa7921}{3}}.|
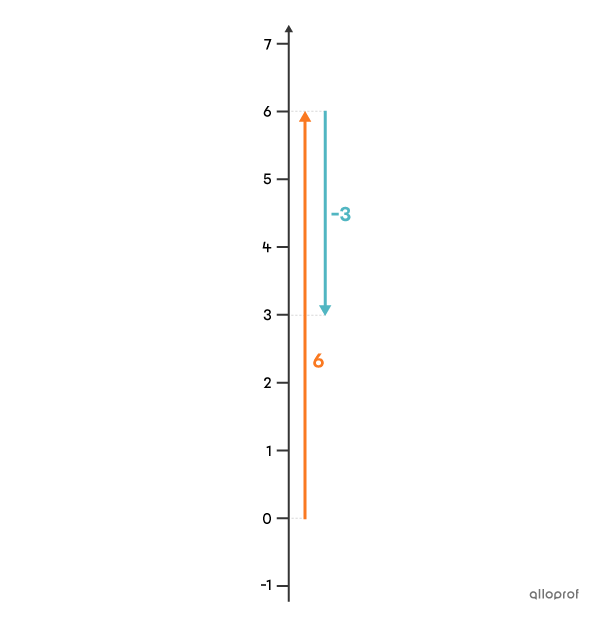
Trouve le résultat de l’addition |-5+4.|
Dans un contexte d’argent, l’addition |\boldsymbol{\color{#51b6c2}{-5}} + \boldsymbol{\color{#fa7921}{4}}| signifie qu’en partant de |0\ \$,| on a une perte de |\boldsymbol{\color{#51b6c2}{5\ \$}},| à laquelle s’ajoute un gain de |\boldsymbol{\color{#fa7921}{4\ \$}}.| Comme la perte est plus grande que le gain, on obtient finalement un montant d’argent négatif, soit une dette.
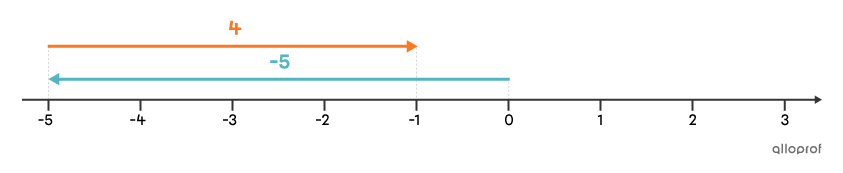
Les 2 termes sont de signes contraires. On fait donc la soustraction |5-4,| et on obtient |1.| Sur la droite, |-5| est le nombre le plus éloigné de |0.| La réponse finale est donc négative.
Réponse : Le résultat de l’addition |-5+4| est |\boldsymbol{\color{#51b6c2}{-1}}.|
La méthode arithmétique pour effectuer une soustraction est semblable à celle pour effectuer une addition. Elle permet également de soustraire des nombres décimaux ou de soustraire des fractions.
Faire la soustraction de 2 nombres revient à faire l’addition du 1er nombre à l’opposé du 2e nombre. Une fois que la soustraction est transformée en addition, on effectue l’opération selon la méthode désirée.
Trouve le résultat de la soustraction |5-20.|
On transforme la soustraction en addition. Puisque l’opposé de |\boldsymbol{\color{#fa7921}{20}}| est |\boldsymbol{\color{#51b6c2}{-20}},| on en déduit que la soustraction |\boldsymbol{\color{#fa7921}{5}}-\boldsymbol{\color{#fa7921}{20}}| est équivalente à l’addition |\boldsymbol{\color{#fa7921}{5}}+\boldsymbol{\color{#51b6c2}{-20}}.| Il s’agit donc d’une addition de termes de signes contraires.
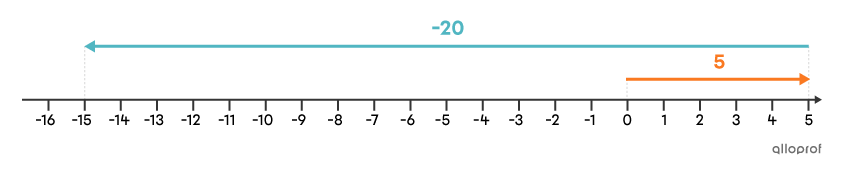
On fait la soustraction |20-5,| et on obtient |15.| Sur la droite, |-20| est le nombre le plus éloigné de |0.| La réponse est donc négative.
Réponse : Le résultat de la soustraction |5-20| est |\boldsymbol{\color{#51b6c2}{-15}}.|
Trouve le résultat de la soustraction |-15- -8.|
On transforme la soustraction en addition. Puisque l’opposé de |\boldsymbol{\color{#51b6c2}{-8}}| est |\boldsymbol{\color{#fa7921}{8}},| on en déduit que la soustraction |\boldsymbol{\color{#51b6c2}{-15}}-\boldsymbol{\color{#51b6c2}{-8}}| est équivalente à l’addition |\boldsymbol{\color{#51b6c2}{-15}}+\boldsymbol{\color{#fa7921}{8}}.| Il s’agit donc d’une addition de termes de signes contraires.
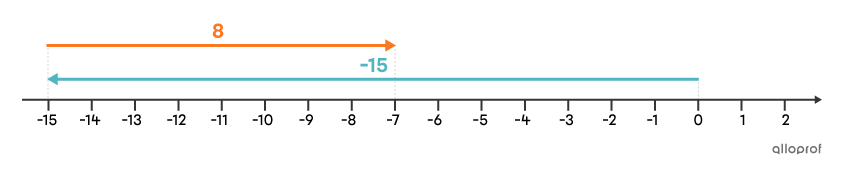
On fait la soustraction |15-8,| et on obtient |7.| Sur la droite, |-15| est le nombre le plus éloigné de |0.| La réponse est donc négative.
Réponse : Le résultat de la soustraction |-15- -8| est |\boldsymbol{\color{#51b6c2}{-7}}.|
Trouve le résultat de la soustraction |-3-6.|
On transforme la soustraction en addition. Puisque l’opposé de |\boldsymbol{\color{#fa7921}{6}}| est |\boldsymbol{\color{#51b6c2}{-6}},| on en déduit que la soustraction |\boldsymbol{\color{#51b6c2}{-3}}-\boldsymbol{\color{#fa7921}{6}}| est équivalente à l’addition |\boldsymbol{\color{#51b6c2}{-3}}+\boldsymbol{\color{#51b6c2}{-6}}.| Il s’agit donc d’une addition de termes négatifs.
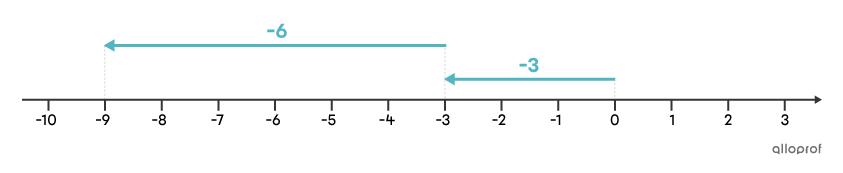
Pour trouver la somme, on additionne les termes sans tenir compte des signes. |3+6| donne |9.| Comme les 2 termes sont négatifs, la somme est également négative.
Réponse : Le résultat de la soustraction |-3-6| est |\boldsymbol{\color{#51b6c2}{-9}}.|
Il arrive que plusieurs signes soient collés dans une opération ou dans une chaine d’opérations. On peut les simplifier avant de commencer les calculs. Voici les différents cas possibles ainsi que leur interprétation dans un contexte d’argent.
|
Additionner un nombre positif revient à faire une addition. |
|4++6 = 4+6 = 10| |
On a |4\ \$| et on ajoute un gain de |6\ \$.| Ça revient à avoir |4\ \$| et à ajouter |6\ \$.| |
|
Additionner un nombre négatif revient à faire une soustraction. |
|4+-6 = 4-6 = -2| |
On a |4\ \$| et on ajoute une dette de |6\ \$.| Ça revient à avoir |4\ \$| et à perdre |6\ \$.| |
|
Soustraire un nombre positif revient à faire une soustraction. |
|4-+6 = 4-6 = -2| |
On a |4\ \$| et on perd un gain de |6\ \$.| Ça revient à avoir |4\ \$| et à perdre |6\ \$.| |
|
Soustraire un nombre négatif revient à faire une addition. |
|4- -6 = 4+6 = 10| |
On a |4\ \$| et on perd une dette de |6\ \$.| Ça revient à avoir |4\ \$| et à ajouter |6\ \$.| |
S’il y a plus de 2 signes collés un à la suite de l’autre et qu’on veut déterminer si l’opération résultante est une addition ou une soustraction, il faut compter le nombre de « |-| ».
-
S’il y en a un nombre pair, l’opération est une addition.
-
S’il y en a un nombre impair, l’opération est une soustraction.
Trouve le résultat de la chaine d’opérations suivante.||(-5{,}5)+-5{,}7-+-3{,}2- (-4)+-1{,}9- - (-4{,}8)||
-
Simplifier les signes
On simplifie ensemble uniquement les signes qui sont collés. On ne tient pas compte des parenthèses.||\begin{alignat}{12}
(-&5{,}5)
&\underbrace{+-}&5{,}7
&\underbrace{-+-}&3{,}2
&\underbrace{-(-}&4)
&\underbrace{+-}&1{,}9
&\underbrace{--(-}&4{,}8)
\\
=-&5{,}5
&-\ \ &5{,}7
&+\ \ \ \ &3{,}2
&+\ \ &4
&-\ \, &1{,}9
&-\ \ \ \ &4{,}8
\end{alignat}|| -
Effectuer les calculs
||\begin{align}&-5{,}5-5{,}7+3{,}2+4-1{,}9-4{,}8\\ = &-11{,}2+3{,}2+4-1{,}9-4{,}8\\ = &-8+4-1{,}9-4{,}8\\ =& -4-1{,}9-4{,}8\\ =&-5{,}9-4{,}8\\=&-10{,}7\end{align}||
Réponse : Le résultat de la chaine d’opérations est |-10{,}7.|
Trouve le résultat de la chaine d’opérations suivante.
||\dfrac{5}{12}-\dfrac{-1}{3}+\dfrac{7}{6}-\dfrac{1}{2}-\dfrac{-7}{-12}||
-
Simplifier les signes
On simplifie ensemble uniquement les signes qui sont collés.||\dfrac{5}{12}+\dfrac{1}{3}+\dfrac{7}{6}-\dfrac{1}{2}-\dfrac{7}{12}|| -
Effectuer les calculs
||\begin{alignat}{13}&&&\dfrac{5}{12}&&+\ \dfrac{1}{3}&&+\ \dfrac{7}{6}&&-\ \dfrac{1}{2}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{5}{12}&&+\dfrac{4}{12}&&+\dfrac{14}{12}&&-\dfrac{6}{12}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{9}{12}&&+\dfrac{14}{12}&&-\dfrac{6}{12}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{23}{12}&&-\dfrac{6}{12}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{17}{12}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{10}{12}\\[3pt]&=&\ &\ \dfrac{5}{6}\end{alignat}||
Réponse : Le résultat de la chaine d’opérations est |\dfrac{5}{6}.|