Addition and subtraction are operations that can be performed with positive numbers, as well as with negative numbers. You need to be comfortable with the whole set of integers. There's a close link between subtraction and addition, since they are inverse operations.
There are several approaches for understanding the addition of positive and negative numbers. The token method and the number line method are visual methods that only work with whole numbers (integers).
The token method is a way of understanding the addition of whole numbers using manipulatives. To use this method, you need tokens of 2 different colours: one for negative numbers and another for positive numbers. A positive token cancels out a negative token. To find the result of the addition, count the remaining number of chips. The colour of the leftover chips indicates the sign of the answer.
Adding 2 Numbers With the Same Sign
The result of adding |-8+-6| can be represented by tokens as follows:
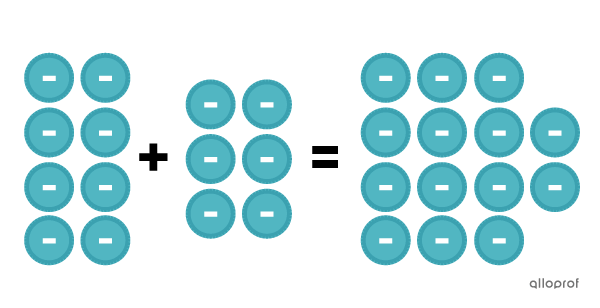
We can't cancel any tokens, since there aren't 2 different colours. So, we add the blue chips together, and find that there are |14.| Since they are blue, which represents the negative chips, we find that the result of the addition |-8+-6| is |-14.|
Adding 2 Numbers With Different Signs
The result of adding |8+-6| can be represented by tokens as follows:
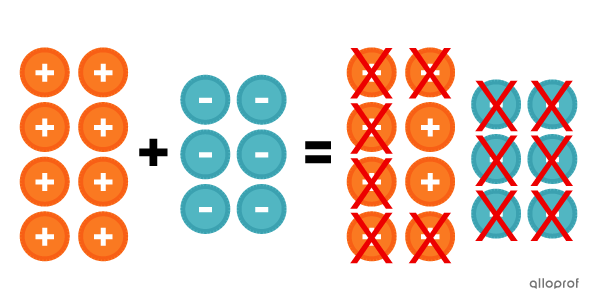
We cancel out each blue chip with an orange chip. Since 2 tokens remain and they are orange, which represents the positive tokens, we find that the result of the addition |8+-6| is |+2,| or simply |2.|
The number line can be used to add integers. To do so, place a point on the line where the 1st term of the addition is located. The 2nd term indicates the number of jumps to be made. If it's positive, we make the jumps to the right, and if it's negative, we make the jumps to the left. The sum is the number reached after all the jumps have been made.
Adding 2 Numbers With Different Signs
The result of the addition |-4+8| can be represented by a number line as follows:
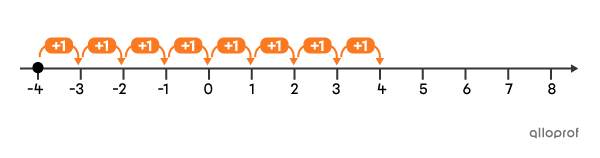
We start by locating the 1st term on the number line with a point at |-4.| The 2nd term of the addition is positive. This indicates that we need to make |8| jumps to the right. We find that the result of the addition |-4+8| is |4.|
Adding 2 Numbers With the Same Sign
The result of the addition |-1+-4| can be represented by a number line as follows:
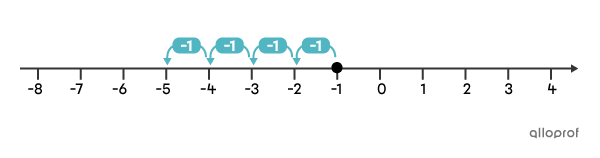
We start by locating the 1st term on the number line with a point at |-1.| The 2nd term of the addition is negative. This indicates that we need to make |4| jumps to the left. We find that the result of the addition |-1+-4| is |-5.|
In general, we use the arithmetic method, which works for more than just integers. This means this method can also be used to add decimal numbers or to add fractions.
This method is based on number sense. A positive number is associated with a positive quantity, and a negative number with a negative quantity. We often use money |(\$)| or temperature |(^\circ \text{C})| contexts to understand these concepts. We imagine that we always start at |0| (like |\$0\ | in a bank account or at |0\ ^\circ \text{C}| on a thermometer). A positive number represents a gain in money or an increase in temperature. A negative number represents a loss of money, or a drop in temperature.
Here are the different cases that may be encountered.
|
Case |
Procedure |
Example |
|---|---|---|
|
The 2 numbers are positive. |
The 2 numbers are added together. The answer is always positive. |
||\boldsymbol{\color{#fa7921}{65}} + \boldsymbol{\color{#fa7921}{17}}=\boldsymbol{\color{#fa7921}{82}}|| |
|
The 2 numbers are negative. |
We add the 2 numbers without taking into account the signs. The answer is always negative. |
||\boldsymbol{\color{#51b6c2}{-24}} + \boldsymbol{\color{#51b6c2}{-18}}=\boldsymbol{\color{#51b6c2}{-42}}|| |
|
The 2 numbers have different signs. |
We subtract the 2 numbers without taking into account their signs. The sign of the answer is the sign of the term that is furthest from |0.| |
||\begin{alignat}{13}\boldsymbol{\color{#51b6c2}{-}}&\boldsymbol{\color{#51b6c2}{22}}&&+\phantom{-}&&\boldsymbol{\color{#fa7921}{8}}&&=\boldsymbol{\color{#51b6c2}{-}}&&\boldsymbol{\color{#51b6c2}{14}}\\&\boldsymbol{\color{#fa7921}{22}}&&+\boldsymbol{\color{#51b6c2}{-}}&&\boldsymbol{\color{#51b6c2}{8}}&&=&&\boldsymbol{\color{#fa7921}{14}}\end{alignat}|| |
Find the result of the addition |6+3.|
In a money context, the addition of |\boldsymbol{\color{#fa7921}{6}} + \boldsymbol{\color{#fa7921}{3}}| means that starting from |\$0,| we have a gain of |\boldsymbol{\color{#fa7921}{\$6\ }}| followed by a gain of |\boldsymbol{\color{#fa7921}{\$3\ }}.| In the end, we end up with even more money.
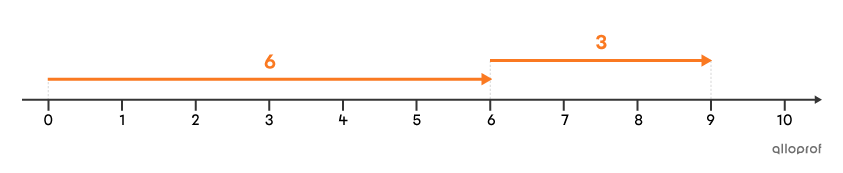
To find the sum, we add |6+3,| and get |\boldsymbol{\color{#fa7921}{9}}.| Since both terms are positive, the sum is also positive.
Answer: The result of adding |6+3| is |\boldsymbol{\color{#fa7921}{9}}.|
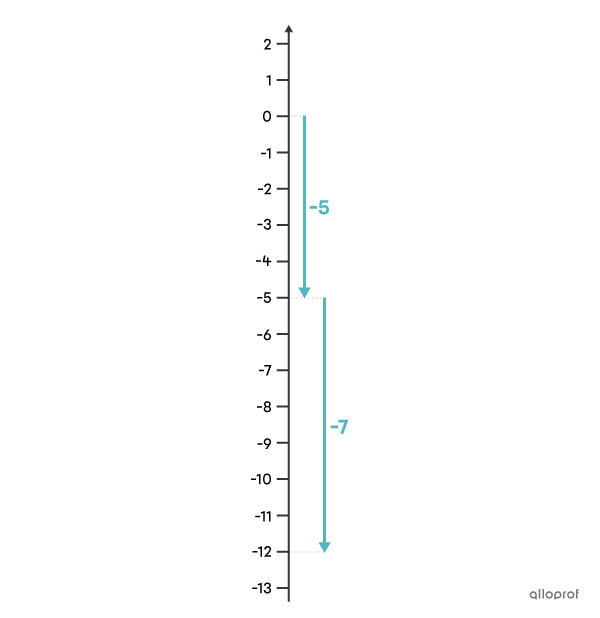
Find the result of the addition |-5+-7.|
In the context of temperature, the addition |\boldsymbol{\color{#51b6c2}{-5}}+\boldsymbol{\color{#51b6c2}{-7}}| means that starting from |0\ ^\circ \text{C},| we have a temperature drop of |\boldsymbol{\color{#51b6c2}{5\ ^\circ \text{C}}},| to which another drop of |\boldsymbol{\color{#51b6c2}{7\ ^\circ \text{C}}}| is added. In other words, the final temperature is even colder than the one measured at the beginning.
To find the sum, we add the terms together without taking the signs into account. |5+7| equals |12.| Since both terms are negative, the sum is also negative.
Answer: The result of adding |-5+-7| is |\boldsymbol{\color{#51b6c2}{-12}}.|
Find the result of the addition |6+-3.|
In the context of temperature, adding |\boldsymbol{\color{#fa7921}{6}} + \boldsymbol{\color{#51b6c2}{-3}}| means that starting from |0\ ^\circ \text{C},| there is a rise in temperature of |\boldsymbol{\color{#fa7921}{6\ ^\circ \text{C}}},| followed by a drop in temperature of |\boldsymbol{\color{#51b6c2}{3\ ^\circ \text{C}}}.| Since the rise in temperature is greater than the drop, we end up with a final temperature that is higher than |0\ ^\circ \text{C}.|
The 2 terms have opposite signs. So we subtract |6-3,| and get |3.| On the right, |6| is the number furthest from |0| (its arrow is the longest). The final answer is therefore positive.
Answer: The result of adding |6+-3| is |\boldsymbol{\color{#fa7921}{3}}.|
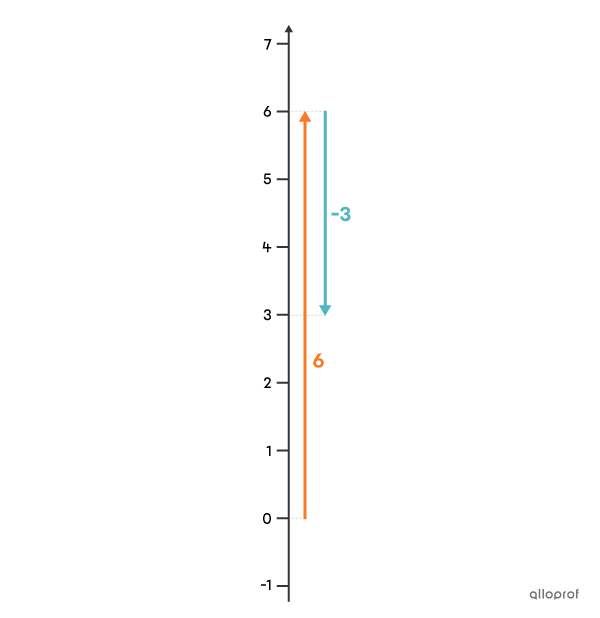
Find the result of the addition |-5+4.|
In the context of money, adding |\boldsymbol{\color{#51b6c2}{-5}} + \boldsymbol{\color{#fa7921}{4}}| means that starting from |\$0,| we have a loss of |\boldsymbol{\color{#51b6c2}{\$5}},| plus a gain of |\boldsymbol{\color{#fa7921}{\$4}}. | Since the loss is greater than the gain, we end up with a negative amount of money, or a debt.

The 2 terms have different signs. So we subtract |5-4,| and get |1.| On the right, |-5| is the number furthest from |0.| The final answer is therefore negative.
Answer: The result of |-5+4| is |\boldsymbol{\color{#51b6c2}{-1}}.|
The arithmetic method for subtraction is similar to the one used for addition. It can also be used to subtract decimal numbers or to subtract fractions.
Subtracting 2 numbers is equivalent to adding the 1st number to the opposite of the 2nd number. Once the subtraction has been transformed into an addition, we carry out the operation using the desired method.
Find the result of the subtraction |5-20.|
We transform the subtraction into an addition. Since the opposite of |\boldsymbol{\color{#fa7921}{20}}| is |\boldsymbol{\color{#51b6c2}{-20}},| we can deduce that the subtraction of |\boldsymbol{\color{#fa7921}{5}}-\boldsymbol{\color{#fa7921}{20}}| is equivalent to the addition of |\boldsymbol{\color{#fa7921}{5}}+\boldsymbol{\color{#51b6c2}{-20}}.| It is therefore a question of adding terms with different signs.
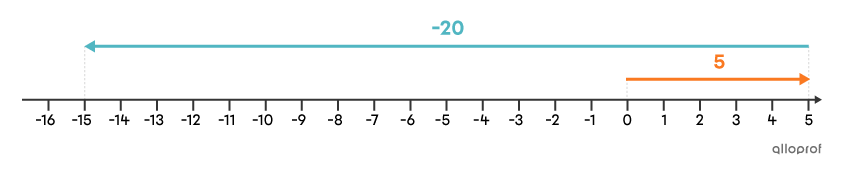
We subtract |20-5,| and obtain |15.| On the number line, |-20| is the number farthest from |0.| The answer is therefore negative.
Answer: The result of subtracting |5-20| is |\boldsymbol{\color{#51b6c2}{-15}}.|
Find the result of the subtraction |-15- -8.|
We transform the subtraction into an addition. Since the opposite of |\boldsymbol{\color{#51b6c2}{-8}}| is |\boldsymbol{\color{#fa7921}{8}},| we can deduce that the subtraction of |\boldsymbol{\color{#51b6c2}{-15}}-\boldsymbol{\color{#51b6c2}{-8}}| is equivalent to the addition of |\boldsymbol{\color{#51b6c2}{-15}}+\boldsymbol{\color{#fa7921}{8}}.| It is therefore a question of adding terms with different signs.

We subtract |15-8,| and get |7.| On the number line, |-15| is the number farthest from |0.| The answer is therefore negative.
Answer: The result of subtracting |-15- -8| is |\boldsymbol{\color{#51b6c2}{-7}}.|
Find the result of the subtraction |-3-6.|
We transform the subtraction into an addition. Since the opposite of |\boldsymbol{\color{#fa7921}{6}}| is |\boldsymbol{\color{#51b6c2}{-6}},| we can deduce that the subtraction of |\boldsymbol{\color{#51b6c2}{-3}}-\boldsymbol{\color{#fa7921}{6}}| is equivalent to the addition of |\boldsymbol{\color{#51b6c2}{-3}}+\boldsymbol{\color{#51b6c2}{-6}}.| It is therefore a problem of adding negative terms.
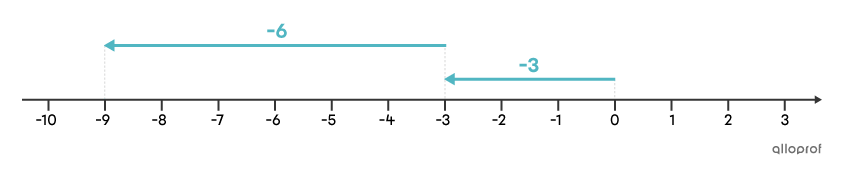
To find the sum, we add the terms without taking their signs into account: |3+6| gives |9.| Since both terms are negative, the sum is also negative.
Answer: The result of subtracting |-3-6| is |\boldsymbol{\color{#51b6c2}{-9}}.|
Sometimes, several signs are stuck together in an operation, or in a chain of operations. These can be simplified before starting the calculation. Here are the possible cases, and their interpretations, in the context of money.
|
Adding a positive number is the same as adding. |
|4++6 = 4+6 = 10| |
We have |\$4| and we add a gain of |\$6.| This is the same as having |\$4| and adding |\$6.| |
|
Adding a negative number is the same as subtracting. |
|4+-6 = 4-6 = -2| |
We have |\$4| and we add a debt of |\$6.| This is the same as having |\$4| and losing |\$6.| |
|
Subtracting a positive number is the same as subtracting. |
|4-+6 = 4-6 = -2| |
We have |\$4| and lose a gain of |\$6.| This is the same as having |\$4| and losing |\$6.| |
|
Subtracting a negative number is the same as adding. |
|4- -6 = 4+6 = 10| |
We have |\$4| and we lose a debt of |\$6.| This is the same as having |\$4| and adding |\$6.| |
If there are more than 2 signs stuck together one after the other, and you want to determine if the resulting operation is an addition or a subtraction, then the number of "|-|" signs need to be counted.
-
If there is an even number, the operation is an addition.
-
If there is an odd number, the operation is a subtraction.
Find the result of the following chain of operations:||(-5.5)+-5.7-+-3.2- (-4)+-1.9- - (-4.8)||
-
Simplify the signs.
We simplify together only the signs that are stuck together. We ignore the brackets.||\begin{alignat}{12} (-&5.5) &\underbrace{+-}&5.7 &\underbrace{-+-}&3.2 &\underbrace{-(-}&4) &\underbrace{+-}&1.9 &\underbrace{--(-}&4.8) \\ =-&5.5 &-\ \ &5.7 &+\ \ \ \ &3.2 &+\ \ &4 &-\ \, &1.9 &-\ \ \ \ &4.8 \end{alignat}|| -
Calculate.||\begin{align}&-5.5-5.7+3.2+4-1.9-4.8\\ = &-11.2+3.2+4-1.9-4.8\\ = &-8+4-1.9-4.8\\ =& -4-1.9-4.8\\ =&-5.9-4.8\\=&-10.7\end{align}||
Answer: The result of the chain of operations is |-10.7.|
Find the result of the following chain of operations:||\dfrac{5}{12}-\dfrac{-1}{3}+\dfrac{7}{6}-\dfrac{1}{2}-\dfrac{-7}{-12}||
-
Simplify the signs.
We simplify only the signs that are stuck together. ||\dfrac{5}{12}+\dfrac{1}{3}+\dfrac{7}{6}-\dfrac{1}{2}-\dfrac{7}{12}|| -
Calculate.||\begin{alignat}{13}&&&\dfrac{5}{12}&&+\ \dfrac{1}{3}&&+\ \dfrac{7}{6}&&-\ \dfrac{1}{2}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{5}{12}&&+\dfrac{4}{12}&&+\dfrac{14}{12}&&-\dfrac{6}{12}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{9}{12}&&+\dfrac{14}{12}&&-\dfrac{6}{12}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{23}{12}&&-\dfrac{6}{12}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{17}{12}&&-\dfrac{7}{12}\\[3pt]&=&\ &\dfrac{10}{12}\\[3pt]&=&\ &\ \dfrac{5}{6}\end{alignat}||
Answer: The result of the chain of operations is |\dfrac{5}{6}.|