Deux paramètres sont présents dans la fonction affine : le paramètre |a,| appelé taux de variation ou pente et le paramètre |b,| appelé ordonnée à l'origine ou valeur initiale.
L'équation d'une fonction affine est :
||f(x) = \color{red}{a}x + \color{blue}{b}||
où |\color{red}{a}| et |\color{blue}{b}| sont des nombres réels.
Dans une relation entre deux variables, le taux de variation (généralement représenté par la lettre |a|) est la comparaison entre deux variations correspondantes de ces variables.
Lorsque deux valeurs sont en relation, une variation des valeurs de la variable indépendante entraine une variation des valeurs correspondantes de la variable dépendante. Il est alors possible de définir le taux de variation de la manière suivante :
||\text{Taux de variation} = \dfrac{\text{Variation de la variable dépendante}}{\text{Variation de la variable indépendante}}||
Ce qui peut être simplifié par l'expression suivante :
||a= \dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1}||
où |(x_1,y_1)| et |(x_2,y_2)| sont deux points distincts de la droite et |\Delta| est la lettre grecque delta représentant une variation.
En géométrie analytique, le taux de variation est nommé pente de la droite.
L'ordonnée à l'origine, aussi appelée valeur initiale et généralement représentée par la lettre |b,| correspond à la valeur de la variable dépendante |(y)| lorsque la valeur indépendante |(x)| vaut |0.| Dans un graphique, l'ordonnée à l'origine correspond au point d'intersection entre la droite et l'axe des ordonnées (l'axe |y|).
Dans l'animation interactive suivante, tu peux modifier la valeur des paramètres |a| et |b| de la fonction affine à l'aide des curseurs. Tu peux aussi déplacer les deux points de la droite directement sur le graphique. Par la suite, tu pourras poursuivre la lecture de la fiche pour savoir comment déterminer le taux de variation |(a)| et la valeur initiale |(b)| à partir de la règle, de la table de valeurs, du graphique ou d'un contexte écrit.
Le taux de variation est représenté par le coefficient de la variable indépendante |(x).|
La valeur initiale est représentée par le terme constant.
Dans l'équation ci-dessous, la lettre |\color{red}{a}| représente le taux de variation et la lettre |\color{blue}{b}| représente la valeur initiale. ||y=\color{red}{a}x+\color{blue}{b}||
Voici quelques exemples d'équations et leurs taux de variation correspondants :
| Équation | Taux de variation | Valeur initiale |
|---|---|---|
| |y=3x-9| | |+3| | |-9| |
| |y=-8x+2| | |-8| | |+2| |
| |y=4+9x| | |+9| | |+4| |
| |y=\frac{1}{2} - \frac{3}{4}x| | |- \frac{3}{4}| | |+\frac{1}{2}| |
| |y=x+7| | |+1| | |+7| |
| |y=-x+8| | |-1| | |+8| |
| |y=78| | |0| | |+78| |
Pour déterminer le taux de variation et la valeur initiale, |y| doit toujours être seul d'un côté de l'équation. Autrement dit, l'équation doit être sous la forme |y=ax+b|. Si ce n'est pas le cas, on doit isoler la variable |y.|
Voici trois exemples où l'on cherche le taux de variation et la valeur initiale :
Exemple 1 : ||\begin{align} 2y &= 4x+8 \\ \frac{2y}{\color{green}{2}} &= \frac{4x}{\color{green}{2}} + \frac{8}{\color{green}{2}} \\ y &= \color{red}{2}x+\color{blue}{4} \end{align}||
Le taux de variation de cette équation est |\color{red}{2}| et sa valeur initiale est |\color{blue}{4}.|
Exemple 2 : ||\begin{align} y+6x &= 7 \\ y+6x \color{green}{-6x} &= 7 \color{green}{-6x} \\ y &= 7-6x \\ y &= \color{red}{-6}x+\color{blue}{7} \end{align}||
Le taux de variation de cette équation est |\color{red}{-6}| et sa valeur initiale est |\color{blue}{7}.|
Exemple 3 : ||\begin{align} \frac{y}{2}-\frac{6x}{5} &= -3 \\ \frac{y}{2}-\frac{6x}{5} \color{green}{+\frac{6x}{5}} &= -3 \color{green}{+\frac{6x}{5}}\\ \frac{y}{2} &= -3 + \frac{6x}{5} \\ \frac{y}{2} \color{green}{\times 2} &= \left(-3 + \frac{6x}{5}\right) \color{green}{\times 2} \\ y &= -6+\frac{12x}{5} \\y &= \color{red}{\frac{12}{5}}x \color{blue}{-6} \end{align}||
Le taux de variation de cette équation est |\color{red}{\dfrac{12}{5}}| et sa valeur initiale est |\color{blue}{-6}.|
Pour calculer le taux de variation et la valeur initiale, il faut suivre les 4 étapes suivantes :
-
Identifier les variables dépendante et indépendante.
-
Choisir 2 points sur la droite ou 2 couples dans la table de valeurs.
-
Appliquer la formule du taux de variation : |a=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2 - y_1}{x_2 - x_1}|
-
Remplacer |a| par la valeur calculée à l'étape précédente ainsi que |x| et |y| par un couple de données, puis isoler |b.|
Remarque : Parfois, on n’a pas à effectuer l'étape 4 pour obtenir la valeur initiale, puisqu’on peut la repérer directement dans le graphique ou dans la table de valeur.
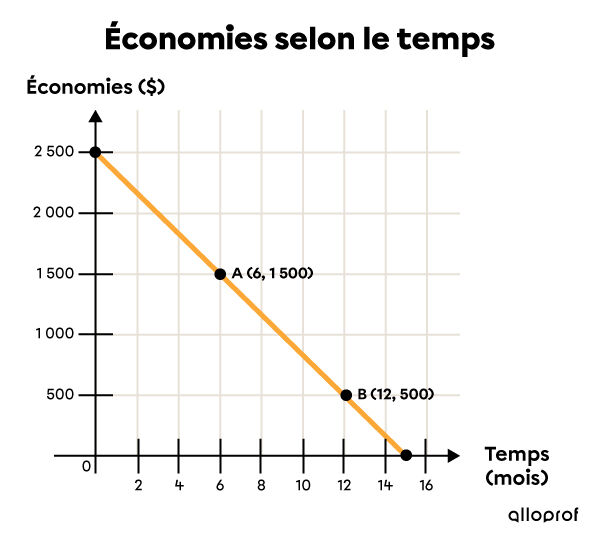
Dans la situation suivante, on considère que les habitudes de consommation de l'individu analysé sont constantes.
-
Combien d’argent cet individu économise-t-il par mois? (taux de variation)
-
Quel est le montant de ses économies au début de l’analyse? (valeur initiale)
-
Identifier les variables dépendante et indépendante
|x=| Temps écoulé (mois)
|y=| Économies |($)| -
Choisir 2 points sur la droite
On peut calculer directement sur le graphique le déplacement vertical |(\color{red}{\Delta y}),| puis horizontal |(\color{#558dec}{\Delta x})| entre les 2 points choisis.
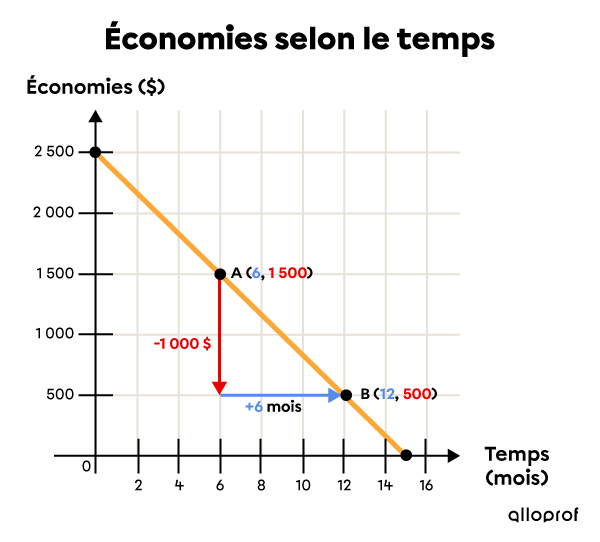
-
Appliquer la formule du taux de variation
Le rapport du déplacement vertical |(\color{red}{\Delta y})| sur le déplacement horizontal |(\color{#558dec}{\Delta x})| donne le taux de variation : ||\begin{align} \color{green}{a} &=\ \dfrac{\color{red}{\Delta y}}{\color{#558dec}{\Delta x}} \\ &=\dfrac{\color{red}{-1000}}{\color{#558dec}{+6}} \\ &= \color{green}{-\dfrac{500}{3}} \\&\approx \color{green}{- 166{,}67}\ \$ / \text{mois} \end{align}||Comme le taux de variation est négatif, cela signifie que les économies de l'individu diminuent d’environ |166{,}67\ $| par mois. Autrement dit, il dépense chaque mois |166{,}67\ $| qu’il puise dans ses économies.
-
Remplacer |\color{green}{a}| par |\color{green}{-166{,}67}| ainsi que |\color{#558dec}{x}| et |\color{red}{y}| par un couple de données, puis isoler |\color{blue}{b}|
La valeur initiale est déjà indiquée clairement sur le graphique : |\color{blue}{2\ 500}\ $|
On n'a donc pas besoin de calculer |\color{blue}{b}.|
La règle de cette situation est : |y= \color{green}{-\dfrac{500}{3}}x + \color{blue}{2\ 500}| ou |y \approx \color{green}{-166{,}67}x + \color{blue}{2\ 500}|
Quel est le taux de variation |(a),| la valeur initiale |(b)| et la règle de la droite illustrée dans le plan cartésien suivant?
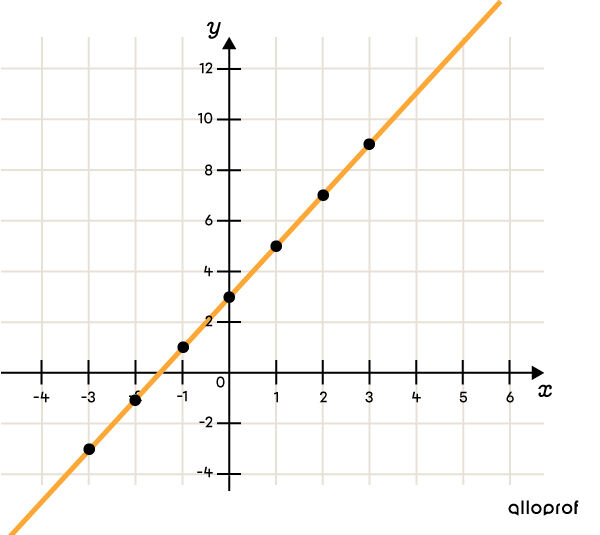
-
Identifier les variables dépendante et indépendante
|x| est la variable indépendante.
|y| est la variable dépendante.Remarque : Ici, on ne peut pas définir les variables d'une façon plus précise puisqu'il s'agit d'une question hors contexte.
-
Sélectionner deux points sur la droite
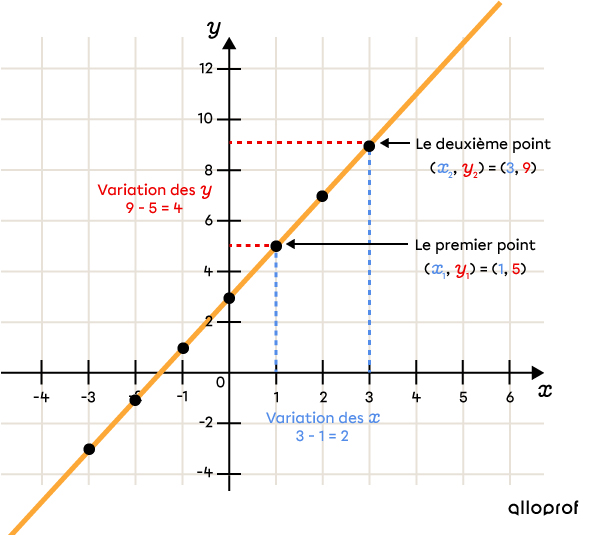
-
Appliquer la formule du taux de variation
||\begin{align} \color{green}{a}=\dfrac{\Delta y}{\Delta x}&= \dfrac{\color{red}{y_2}-\color{red}{y_1}}{\color{#548de9}{x_2}-\color{#548de9}{x_1}}\\&=\dfrac{\color{red}{9}-\color{red}{5}}{\color{#548de9}{3}-\color{#548de9}{1}} \\ &= \dfrac{4}{2} \\ &= \color{green}{2} \end{align}||Le taux de variation de ce graphique est |\color{green}{2}.|
La valeur initiale est entre |2| et |4| si on observe le graphique. On peut supposer que c’est |3,| mais il serait préférable de faire les calculs pour s’en assurer.
-
Remplacer |\color{green}{a}| par |\color{green}{2}| ainsi que |\color{#548de9}{x}| et |\color{red}{y}| par les coordonnées d’un point, puis isoler |\color{blue}{b}| ||\begin{align} y &= \color{green}{a}x + \color{blue}{b} \\ \color{red}{y} &= \color{green}{2}\color{#548de9}{x}+\color{blue}{b} \\ \color{red}{9} &= 2(\color{#548de9}{3}) +\color{blue}{b} \\ 9 &= 6 + \color{blue}{b} \\ 9\color{magenta}{-6} &= 6 \color{magenta}{-6} + \color{blue}{b} \\ \color{blue}{3} &= \color{blue}{b} \end{align}||La valeur initiale est bel et bien |\color{blue}{3}.|
La règle est : |y = \color{green}{2}x + \color{blue}{3}|
Pour calculer le taux de variation et la valeur initiale à partir d'une table de valeurs, il faut suivre la même procédure que si on le fait à partir d'un graphique. D'ailleurs, on peut tracer le graphique pour s'aider.
Marc vient de s’ouvrir un magasin d’impression. Il a acheté une photocopieuse haute performance. Il a établi les couts ci-dessous pour l’utilisation de son photocopieur.
| Nombre de photocopies | |5| | |10| | |15| | |20| | |40| | |75| |
|---|---|---|---|---|---|---|
| Montant à débourser |($)| | |0{,}65\ $| | |1{,}30\ $| | |1{,}95\ $| | |2{,}60\ $| | |5{,}20\ $| | |9{,}75\ $| |
-
Quel est le prix par photocopie?
-
Quel est le prix initial?
-
Identifier les variables dépendante et indépendante
|x=| Nombre de photocopies
|y=| Montant à débourser -
Choisir deux couples dans la table de valeurs
Couple 1 : |10| photocopies pour |1{,}30\ $ = \underset{\color{navy}{\Large{(x_1\ ; \ \ y_1)\ \ }}}{\color{navy}{(10\ ; 1{,}30)}}|
Couple 2 : |40| photocopies pour |5{,}20\ $ = \underset{\color{green}{\Large{(x_2\ ; \ \ y_2)\ \ }}}{\color{green}{(40\ ; 5{,}20)}}|
-
Appliquer la formule du taux de variation
||\begin{align}\color{red}{a}=\frac{\Delta y}{\Delta x}&= \dfrac{\color{green}{y_2}-\color{navy}{y_1}}{\color{green}{x_2}-\color{navy}{x_1}}\\&=\dfrac{\color{green}{5{,}20}-\color{navy}{1{,}30}}{\color{green}{40}-\color{navy}{10}} \\ &= \dfrac{3{,}90}{30} \\ &= \color{red}{0{,}13} \end{align}||
Dans cette situation, le taux de variation correspond au cout par photocopie. Ainsi, il en coute |\color{red}{0{,}13}\ $| par photocopie.
-
Remplacer |\color{red}{a}| par |\color{red}{0{,}13}| ainsi que |\color{navy}{x}| et |\color{navy}{y}| par un couple de données, puis isoler |\color{blue}{b}|
Ici, on choisit le couple |\color{navy}{(x,y)} = \color{navy}{(10\ ; 1{,}30)},| mais on aurait pu sélectionner n’importe quel autre couple de la table de valeurs. ||\begin{align} y &= \color{red}{a}x+\color{blue}{b} \\ \color{navy}{y} &= \color{red}{0{,}13}\color{navy}{x}+\color{blue}{b} \\ \color{navy}{1{,}30} &= 0{,}13(\color{navy}{10}) +\color{blue}{b} \\ 1{,}30 &= 1{,}30 + \color{blue}{b} \\ \color{blue}{0} &= \color{blue}{b} \end{align}||
La valeur initiale, c'est-à-dire le prix initial, est de |\color{blue}{0}\ $.| Il s’agit donc d’une situation de variation directe, aussi appelée fonction linéaire ou situation de proportionnalité.
La règle de cette situation est donc : |y=\color{red}{0{,}13}x|
Ginette enlève le bouchon de sa baignoire, puis elle note le niveau d’eau dans le bain toutes les 2 minutes. Voici les données qu’elle recueille :
| Temps écoulé (min) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| Niveau d’eau (cm) | 30 | 22 | 14 | 6 |
-
À quelle vitesse le niveau d’eau dans la baignoire diminue-t-il? (taux de variation)
-
Quel était le niveau d’eau dans le bain au moment où Ginette a retiré le bouchon? (valeur initiale)
-
Identifier les variables dépendante et indépendante
|x=| Temps écoulé (min)
|y=| Niveau d’eau (cm) -
Choisir deux couples dans la table de valeurs
Couple 1 : Niveau à 30 cm après 2 minutes |= \underset{\color{navy}{\large{(x_1 ,\ y_1)}}}{\color{navy}{(2\ , 30)}}|
Couple 2 : Niveau à 6 cm après 8 minutes |= \underset{\color{green}{\large{(x_2,\ y_2)}}}{\color{green}{(8 , 6)}}|
-
Appliquer la formule du taux de variation ||\begin{align}\color{red}{a}=\dfrac{\Delta y}{\Delta x}&= \dfrac{\color{green}{y_2}-\color{navy}{y_1}}{\color{green}{x_2}-\color{navy}{x_1}}\\&=\dfrac{\color{green}{6}-\color{navy}{30}}{\color{green}{8}-\color{navy}{2}} \\ &= \dfrac{-24}{6} \\ &= \color{red}{-4} \end{align}||Dans cette situation, le taux de variation correspond à la vitesse à laquelle le niveau d’eau diminue, puisque |\color{red}{a}| est négatif. Ainsi, le niveau d’eau baisse de |4\ \text{cm}| par minute.
-
Remplacer |\color{red}{a}| par |\color{red}{-4}| ainsi que |x| et |y| par un couple de données, puis isoler |\color{blue}{b}|
Ici, on choisit le couple |(x,y) = (6,14).| ||\begin{align} y &= \color{red}{a}x+\color{blue}{b} \\ y &= \color{red}{-4}x+\color{blue}{b} \\ 14 &= -4(6) +\color{blue}{b} \\ 14 &= -24+\color{blue}{b} \\ 14 \color{red}{+24} &= -24 \color{red}{+24} +\color{blue}{b} \\ \color{blue}{38} &= \color{blue}{b} \end{align}||La valeur initiale est de |\color{blue}{38}\ \text{cm}.| Il s’agit du niveau d’eau dans la baignoire au moment où Ginette a retiré le bouchon, soit à |0| minute.
Puisque la valeur initiale est différente de |0,| il s’agit d’une fonction affine de variation partielle.
La règle de cette situation est donc : |y=\color{red}{-4}x+\color{blue}{38}|
Dans une mise en situation, il arrive assez souvent que le taux de variation et la valeur initiale soient donnés directement. Dans ce cas, on peut les déduire sans avoir à effectuer le moindre calcul.
Au début de son dernier voyage, la voiture de Jean-Pierre affichait |125\ 000| km au compteur. Sachant qu’il a conservé une vitesse moyenne de |100| km/h, quel sera le kilométrage total de sa voiture après |22| heures de conduite?
Dans cet énoncé de problème, le taux de variation et la valeur initiale sont donnés directement. On n’a pas à les calculer.
Puisqu’une vitesse est un taux, la vitesse moyenne correspond au taux de variation. Ainsi, |\color{red}{a=100}| km/h.
La valeur initiale correspond à la valeur au début d’une expérience ou d’une mise en situation. Ici, la valeur initiale est donnée directement. Il s’agit du kilométrage au tout début du voyage. Ainsi, |\color{blue}{b= 125\ 000}| km.
La règle représentant cette situation est donc : |y=\color{red}{100}x + \color{blue}{125\ 000}| où |x| est le nombre d’heures de conduite depuis le début du voyage et |y| est le kilométrage total au compteur (km).
De ce fait, pour répondre à la question, il ne reste qu’à remplacer |x| par |22,| puis à faire le calcul pour trouver la valeur de |y| correspondante.
Si le prix de l’essence était de |1{,}12\ $\text{/L}| au moment où je suis allé faire le plein, combien de litres ai-je mis dans le réservoir de ma voiture si j’ai dû payer |56\ $?|
Comme le prix de l’essence est exprimé sous la forme d’un taux, il s’agit du taux de variation dans cette situation. Ainsi, |\color{red}{a=1{,}12}\ $\text{/L}.|
La valeur initiale n’est pas donnée explicitement dans l’énoncé du problème, mais on peut quand même la déduire si on identifie correctement le type de situation auquel on a affaire. Le cout de l’essence est une situation de variation directe, aussi appelée situation de proportionnalité. Si on traçait le graphique d’une telle situation, on aurait une droite qui commence au point |(0,0).| Autrement dit, la valeur initiale vaut zéro. En effet, lorsqu’on met |0| litre d’essence, on ne paye rien! Il n’y a pas de prix de départ dans une telle situation. Ainsi, |\color{blue}{b=0}.|
La règle est donc : |y=\color{red}{1{,}12}x,| où |x| est le nombre de litres d’essence achetés et |y| est le cout total de la transaction |($).|
De ce fait, pour répondre à la question, il ne reste qu’à remplacer |y| par |56,| puis à isoler |x.|
Dans d’autres mises en situation, il faut former des couples de coordonnées et calculer le taux de variation à partir de ceux-ci. On calcule ensuite la valeur initiale après avoir remplacé |a,| |x| et |y| dans la règle d’une fonction affine. Autrement dit, il faut suivre la même procédure que lorsqu'on a le graphique de la situation.
Rodolphe est en camping. Il se réveille à 7 h et il note que la température à l’intérieur de sa tente est de 15 ºC. À 11 h, il note que la température à l’intérieur de sa tente est maintenant de 21 ºC.
-
De combien de degrés la température intérieure de sa tente a-t-elle augmenté en moyenne par heure au courant de la matinée?
-
Quelle est la valeur initiale et que représente-t-elle dans cette situation?
-
Identifier les variables dépendante et indépendante
|x=| le nombre d'heures
|y=| la température (°C) -
Chercher deux couples de données dans le texte
À 7 h, la température est de 15 ºC : |(7, 15).|
À 11 h, la température est de 21 ºC : |(11, 21).| -
Appliquer la formule du taux de variation ||\begin{align} \color{red}{a} = \frac{\Delta x}{\Delta y} &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{21-15}{11-7} \\ &= \frac{6}{4} \\ &= \color{red}{1{,}5}\ ^{\circ}\text{C} / \text{h} \end{align}||Le taux de variation est de |\color{red}{1{,}5}\ ^{\circ}\text{C} / \text{h}.|
-
Remplacer |\color{red}{a}| par |\color{red}{1{,}5}| ainsi que |\color{green}{x}| et |\color{green}{y}| par les coordonnées d’un point, puis isoler |\color{blue}{b}| ||\begin{align} y &= \color{red}{a}x + \color{blue}{b} \\ \color{green}{y} &= \color{red}{1{,}5}\color{green}{x} + \color{blue}{b} \\ \color{green}{15} &= 1{,}5(\color{green}{7}) + \color{blue}{b} \\ 15 &= 10{,}5 + \color{blue}{b} \\ 15\color{magenta}{-10{,}5} &= 10{,}5 \color{magenta}{-10{,}5} + \color{blue}{b} \\ \color{blue}{4{,}5} &= \color{blue}{b} \end{align}||La valeur initiale est de |\color{blue}{4{,}5}\ ^{\circ}\text{C}.| Cette valeur correspond à la température qu’on aurait mesurée à |0\ \text{h}| (minuit) si la température suivait déjà cette tendance à ce moment-là.
La règle est : |y=\color{red}{1{,}5}x+\color{blue}{4{,}5}|
Un réservoir d’eau de 100 litres se vide à un rythme régulier en 8 minutes.
Représente la situation par un graphique, puis donne le taux de variation, la valeur initiale et la règle de cette situation.
-
Identifier les variables dépendante et indépendante
|x=| Temps écoulé (min)
|y=| Quantité d’eau (L) -
Sélectionner 2 points sur la droite
Afin de sélectionner les 2 points, on peut d'abord tracer le graphique, ce qui permet de bien visualiser la situation.
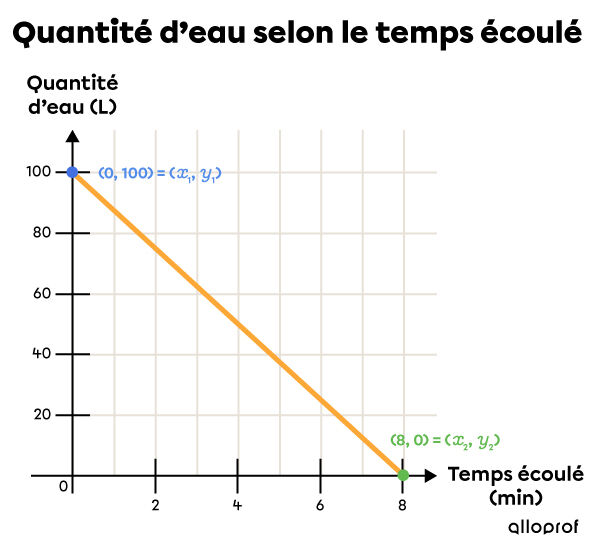
Puisque le réservoir contient |100\ \text{L}| d’eau au moment où on commence à le vider, soit à |0| minutes, on a le point |(0, 100).| Ce point est l’ordonnée à l’origine (la valeur initiale).
Étant donné qu’il faut |8| minutes pour vider le réservoir complètement |(\text{vide}=0\ \text{L}),| on a le point |(8,0).| Ce point est l’abscisse à l’origine, soit le point de la droite qui est situé sur l’axe des |x.|
-
Appliquer la formule du taux de variation ||\begin{align} \color{red}{a} = \dfrac{\Delta y}{\Delta x} &= \dfrac{\color{green}{y_2} - \color{blue}{y_1}}{\color{green}{x_2} - \color{blue}{x_1}} \\ &= \dfrac{\color{green}{0} - \color{blue}{100}}{\color{green}{8} - \color{blue}{0}} \\ &= \dfrac{-100}{8} \\ &= \color{red}{-12{,}5}\ \text{L/min} \end{align}||Le taux de variation est de |\color{red}{-12{,}5}\ \text{L/min}.| Ce taux est négatif, ce qui est normal puisque le réservoir se vide.
-
Remplacer |\color{red}{a}| par |\color{red}{-12{,}5}| ainsi que |x| et |y| par les coordonnées d’un point, puis isoler |\color{blue}{b}|
La valeur initiale était déjà donnée dans l'énoncé du problème. Il s'agit de la quantité initiale d'eau dans le réservoir, soit |\color{blue}{100}\ \text{L}.| Il n'est donc pas nécessaire de faire l'étape 4.
La règle est : |y=\color{red}{-12{,}5}x + \color{blue}{100}|