La fonction polynomiale de degré 2 (ou fonction quadratique) peut s’écrire sous différentes formes. Lorsqu’on veut trouver la règle, on doit choisir la forme appropriée selon le contexte.
||f(x)=ax^2||
Pour trouver la règle, il faut seulement connaitre les coordonnées d’un point de la parabole. Voici comment procéder.
-
Remplacer |x| et |f(x)| dans l’équation par les coordonnées d’un point.
-
Isoler le paramètre |a.|
-
Donner la règle.
Trouve la règle de la fonction polynomiale de degré 2 qui passe par le point |(-3;40{,}5).|
-
Remplacer |x| et |f(x)| dans l’équation par les coordonnées d’un point
||\begin{align}f(x)&=ax^2\\\color{#3a9a38}{40{,}5}&=a(\color{#3a9a38}{-3})^2\end{align}|| -
Isoler le paramètre |a|
||\begin{align}40{,}5&=a(-3)^2\\ 40{,}5&=9a\\\dfrac{40{,}5}{\color{#ec0000}9}&=\dfrac{9a}{\color{#ec0000}9}\\ 4{,}5&=a\end{align}|| -
Donner la règle
La règle de la fonction est |f(x)=4{,}5x^2.|
Trouve la règle de la fonction polynomiale de degré 2 qui passe par le point |(1{,}5;-11{,}25).|
-
Remplacer |x| et |f(x)| dans l’équation par les coordonnées d’un point
||\begin{align}f(x)&=ax^2\\\color{#3a9a38}{-11{,}25}&=a(\color{#3a9a38}{1{,}5})^2\end{align}|| -
Isoler le paramètre |a|
||\begin{align}-11{,}25&=a(1{,}5)^2\\ -11{,}25&=2{,}25a\\\dfrac{-11{,}25}{\color{#ec0000}{2{,}25}}&=\dfrac{2{,}25a}{\color{#ec0000}{2{,}25}}\\ -5&=a\end{align}|| -
Donner la règle
La règle de la fonction est |f(x)=-5x^2.|
Il existe plusieurs méthodes possibles pour trouver la règle d’une fonction polynomiale de degré 2 décentrée. Tout dépend des informations qui sont fournies.
Lorsqu'on connait le sommet de la fonction ainsi qu'un autre point par lequel elle passe, il faut utiliser la forme canonique. En effet, la coordonnée en |x| du sommet correspond au paramètre |h,| alors que la coordonnée en |y| correspond au paramètre |k.|
||f(x)=a(x-h)^2+k||où
|(h,k)| : coordonnées du sommet
Voici comment procéder pour trouver la règle.
-
Remplacer |h| et |k| dans l'équation par les coordonnées du sommet.
-
Remplacer |x| et |f(x)| dans l'équation par les coordonnées d’un point autre que le sommet.
-
Isoler le paramètre |a.|
-
Donner la règle.
Trouve la règle de la fonction polynomiale de degré 2 dont le sommet est aux coordonnées |(4,6)| et qui passe par le point |(2,-2).|
-
Remplacer |h| et |k| dans l'équation par les coordonnées du sommet
||\begin{align}f(x)&=a(x-h)^2+k\\ f(x)&=a(x-\color{#fa7921}4)^2+\color{#3b87cd}6\end{align}|| -
Remplacer |x| et |f(x)| dans l'équation par les coordonnées d’un point autre que le sommet
||\begin{align}f(x)&=a(x-4)^2+6\\ \color{#3a9a38}{-2}&=a(\color{#3a9a38}2-4)^2+6\end{align}|| -
Isoler le paramètre |a|
||\begin{align}-2&=a(2-4)^2+6\\ -2&=a(-2)^2+6\\ -2&=4a+6\\ -8&=4a\\ -2&=a\end{align}|| -
Donner la règle
La règle de la fonction est |f(x)=-2(x-4)^2+6.|
Trouve la règle de la fonction polynomiale de degré 2 dont le sommet est aux coordonnées |(-1,2)| et qui passe par le point |(3,26).|
-
Remplacer |h| et |k| dans l'équation par les coordonnées du sommet
||\begin{align}f(x)&=a(x-h)^2+k\\ f(x)&=a(x-\color{#fa7921}{-1})^2+\color{#3b87cd}2\end{align}|| -
Remplacer |x| et |f(x)| dans l'équation par les coordonnées d’un point autre que le sommet
||\begin{align}f(x)&=a(x+1)^2+2\\ \color{#3a9a38}{26}&=a(\color{#3a9a38}3+1)^2+2\end{align}|| -
Isoler le paramètre |a|
||\begin{align}26&=a(3+1)^2+2\\ 26&=a(4)^2+2\\ 26&=16a+2\\ 24&=16a\\ 1{,}5&=a\end{align}|| -
Donner la règle
La règle de la fonction est |f(x)=1{,}5(x+1)^2+2.|
Lorsqu'on connait les 2 zéros de la fonction ainsi qu’un autre point par lequel elle passe, il faut utiliser la forme factorisée. Les zéros correspondent aux paramètres |x_1| et |x_2| dans la règle.
||f(x)=a(x-x_1)(x-x_2)||où
|x_1| et |x_2| : zéros (abscisses à l’origine)
Voici comment procéder pour trouver la règle.
-
Remplacer |x_1| et |x_2| dans l’équation par les zéros.
-
Remplacer |x| et |f(x)| dans l’équation par les coordonnées d’un autre point que les zéros.
-
Isoler le paramètre |a.|
-
Donner la règle.
L’ordre dans lequel on place |x_1| et |x_2| dans la règle n’a pas d’importance.
Trouve la règle de la fonction polynomiale de degré 2 dont les zéros sont |-3| et |8| et qui passe par le point |(5,-24).|
-
Remplacer |x_1| et |x_2| dans l’équation par les zéros
||\begin{align}f(x)&=a(x-x_1)(x-x_2)\\f(x)&=a(x-\color{#ff55c3}{-3})(x-\color{#ff55c3}8)\end{align}|| -
Remplacer |x| et |f(x)| dans l’équation par les coordonnées d’un autre point que les zéros
||\begin{align}f(x)&=a(x+3)(x-8)\\\color{#3a9a38}{-24}&=a(\color{#3a9a38}5+3)(\color{#3a9a38}5-8)\end{align}|| -
Isoler le paramètre |a|
||\begin{align}-24&=a(5+3)(5-8)\\-24&=a(8)(-3)\\ -24&=-24a\\1&=a\end{align}|| -
Donner la règle
La règle de la fonction est |f(x)=(x+3)(x-8).|
Trouve la règle en forme générale de la fonction polynomiale de degré 2 qui passe par les points |(-2,0),| |(7,18)| et |(3,0).|
Comme il n’est pas possible de déterminer directement la règle sous la forme générale avec les zéros, on trouve d’abord la règle sous la forme factorisée, puis on la transforme.
-
Remplacer |x_1| et |x_2| dans l’équation par les zéros
Grâce aux points |(-2,0)| et |(3,0),| on déduit que les zéros de la fonction sont |-2| et |3.|||\begin{align}f(x)&=a(x-x_1)(x-x_2)\\ f(x)&=a(x-\color{#ff55c3}{-2})(x-\color{#ff55c3}3)\end{align}|| -
Remplacer |x| et |f(x)| dans l’équation par les coordonnées d’un autre point que les zéros
||\begin{align}f(x)&=a(x+2)(x-3)\\ 18&=a(\color{#3a9a38}7+2)(\color{#3a9a38}7-3)\end{align}|| -
Isoler le paramètre |a|
||\begin{align}18&=a(7+2)(7-3)\\ 18&=a(9)(4)\\ 18&=36a\\ 0{,}5&=a\end{align}|| -
Donner la règle
La règle de la fonction sous la forme factorisée est |f(x)=0{,}5(x+2)(x-3).|
Pour la transformer en forme générale, on doit développer l’expression. ||\begin{align}f(x)&=0{,}5(x+2)(x-3)\\ &= 0{,}5(x^2-3x+2x-6)\\&= 0{,}5(x^2-x-6)\\ &= 0{,}5x^2-0{,}5x-3 \end{align}||La règle de la fonction sous forme générale est |f(x)=0{,}5x^2-0{,}5x-3.|
Lorsqu’on connait 2 points de la fonction qui ont la même ordonnée (même coordonnée en |y|), il est possible de trouver la règle sous la forme canonique |\left(f(x)=a(x-h)^2+k\right).|
La parabole possède un axe de symétrie vertical qui passe par son sommet. Ainsi, 2 points qui ont la même ordonnée sont à égale distance de l’axe de symétrie |x=h.| Il est donc possible de faire la moyenne des coordonnées en |x| de ces points pour trouver la valeur de |h.|||h=\dfrac{x_A+x_B}{2}||
où
|x_A| et |x_B| : abscisses des 2 points ayant la même ordonnée

Cas 1 : lorsque la coordonnée |\boldsymbol{y}| du sommet est connue
-
Calculer la valeur de |h| à l'aide de la formule.
-
Vérifier si le point dont |h| est la coordonnée en |x| est donné. Si oui, ce point est le sommet. Si non, se référer au cas 2.
-
Remplacer |h| et |k| dans l’équation canonique par les coordonnées du sommet.
-
Remplacer |x| et |f(x)| dans l'équation par les coordonnées d'un point différent du sommet.
-
Isoler |a.|
-
Donner la règle.
Trouve l'équation de la fonction polynomiale de degré 2 représentée dans la table de valeurs ci-dessous.
| |x| | |-4| | |-3| | |-1| | |0| | |2| |
|---|---|---|---|---|---|
| |y| | |4| | |-1| | |-5| | |-4| | |4| |
-
Calculer la valeur de |h|
On remarque que les points |(-4,4)| et |(2,4)| ont la même coordonnée en |y.| On peut donc calculer |h| à partir de leur coordonnée en |x.|||\begin{align}\color{#fa7921}h&=\dfrac{x_A+x_B}{2}\\ &=\dfrac{-4+2}{2}\\&=\dfrac{-2}{2}\\ &=\color{#fa7921}{-1}\end{align}|| -
Vérifier si le point dont |h| est la coordonnée en |x| est donné
On remarque que |-1| est la coordonnée en |x| d’un des points de la table de valeurs. On en déduit que |(-1,5)| est le sommet de la parabole, donc |\color{#3b87cd}k=\color{#3b87cd}{-5}.| -
Remplacer |h| et |k| dans l’équation par les coordonnées du sommet
||\begin{align}f(x)&=a(x-h)^2+k\\ f(x)&=a(x-\color{#fa7921}{-1})^2+\color{#3b87cd}{-5}\end{align}|| -
Remplacer |x| et |f(x)| dans l'équation par les coordonnées d'un point différent du sommet
On utilise le point |(-4,4).|||\begin{align}f(x)&=a(x+1)^2-5 \\ \color{#3a9a38}{4}&=a(\color{#3a9a38}{-4}+1)^2-5\end{align}|| -
Isoler |a|
||\begin{align}4&=a(-3)^2-5\\4&=9a-5\\9&=9a\\1&=a\end{align}|| -
Donner la règle
La règle de la fonction est |f(x)=(x+1)^2-5.|
Cas 2 : lorsque la coordonnée |\boldsymbol{y}| du sommet est inconnue
Dans ces situations, on se retrouve avec 2 inconnues : les paramètres |a| et |k.| Il faut donc créer un système d’équations et le résoudre.
-
Calculer la valeur de |h| à l'aide de la formule.
-
Remplacer |h| dans l’équation par la valeur trouvée à l’étape précédente.
-
Créer un système d’équations en remplaçant |x| et |f(x)| par les coordonnées de 2 points. Il ne faut pas que les 2 points soient ceux de même ordonnée.
-
Résoudre le système d’équation pour trouver la valeur de |a| et |k.|
-
Donner la règle.
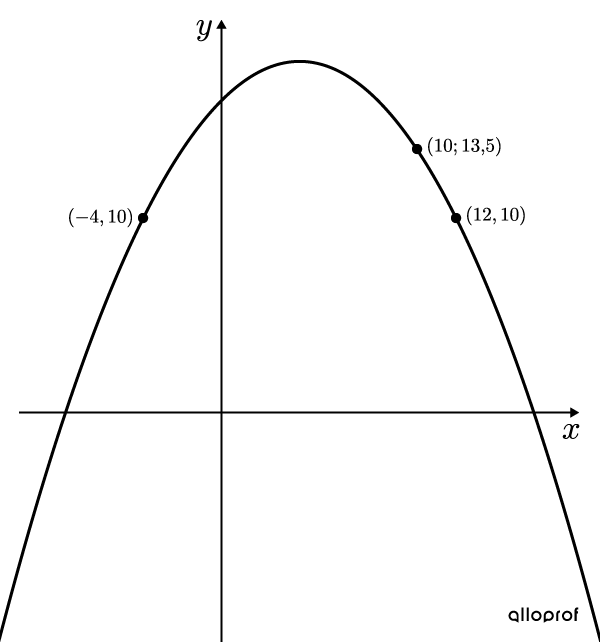
Trouve l'équation de la fonction polynomiale de degré 2 représentée ci-dessous.
-
Calculer la valeur de |h|
||\begin{align}\color{#fa7921}h&=\dfrac{x_A+x_B}{2}\\ &=\dfrac{-4+12}{2}\\&=\dfrac{8}{2}\\ &=\color{#fa7921}4\end{align}|| -
Remplacer |h| dans l’équation
||\begin{align}f(x)&= a(x-h)^2+k\\ &=a(x-\color{#fa7921}{4})^2+k \end{align}|| -
Créer un système d’équations avec 2 points
Équation 1||\begin{align} \color{#3a9a38}{f(x)}&=a(\color{#3a9a38}{x}-4)^2+k\\ \color{#3a9a38}{10}&=a(\color{#3a9a38}{-4}-4)^2+k\\ 10&=a(-8)^2+k\\ 10&=64a+k\end{align}||
Équation 2||\begin{align}\color{#3a9a38}{f(x)}&=a(\color{#3a9a38}{x}-4)^2+k\\\color{#3a9a38}{13{,}5}&=a(\color{#3a9a38}{10}-4)^2+k\\13{,}5&=a(6)^2+k\\13{,}5&=36a+k\end{align}||
-
Résoudre le système d’équations pour trouver la valeur de |a| et |k|
On commence par isoler |k| dans la première équation pour utiliser la méthode de substitution.||\begin{align}10&=64a+k\\\color{#3b87cd}{10-64a}&=\color{#3b87cd}k\end{align}||On remplace |k| dans la deuxième équation par cette expression.||\begin{align}13{,}5&=36a+\color{#3b87cd}k\\13{,}5&=36a+ \color{#3b87cd}{10-64a}\\13{,}5&=-28a+10\\3{,}5&=-28a\\\color{#3a9a38}{-0{,}125}&=\color{#3a9a38}a\end{align}||Il ne reste plus qu’à trouver la valeur de |k.| On utilise l’équation dans laquelle |k| est isolée.||\begin{align}k&=10-64\color{#3a9a38}{a}\\&=10-64(\color{#3a9a38}{-0{,}125})\\&=10--8\\&=18\end{align}|| -
Donner la règle
La règle de la fonction est |f(x)=-0{,}125(x-4)^2+18.|