The quadratic function (or second-degree polynomial function) can be written in different forms. When we want to find the rule, we must choose the appropriate form according to the context.
||f(x)=ax^2||
We can find the rule by simply knowing the coordinates of a point on the parabola. Here's how.
-
Replace |x| and |f(x)| in the equation with the coordinates of a point.
-
Isolate parameter |a.|
-
Give the rule.
Find the rule of the quadratic function that passes through point |(-3,40.5).|
-
Replace |x| and |f(x)| in the equation with the coordinates of a point
||\begin{align}f(x)&=ax^2\\\color{#3a9a38}{40.5}&=a(\color{#3a9a38}{-3})^2\end{align}|| -
Isolate parameter |a|
||\begin{align}40.5&=a(-3)^2\\ 40.5&=9a\\\dfrac{40.5}{\color{#ec0000}9}&=\dfrac{9a}{\color{#ec0000}9}\\ 4.5&=a\end{align}|| -
Give the rule
The function rule is |f(x)=4.5x^2.|
Find the rule of the quadratic function with a point at |(1.5,-11.25).|
-
Replace |x| and |f(x)| in the equation with the coordinates of a point
||\begin{align}f(x)&=ax^2\\\color{#3a9a38}{-11.25}&=a(\color{#3a9a38}{1.5})^2\end{align}|| -
Isolate parameter |a|
||\begin{align}-11.25&=a(1.5)^2\\ -11.25&=2.25a\\\dfrac{-11.25}{\color{#ec0000}{2.25}}&=\dfrac{2.25a}{\color{#ec0000}{2.25}}\\ -5&=a\end{align}|| -
Give the rule
The function rule is |f(x)=-5x^2.|
There are several possible methods for finding the rule of a quadratic function when the vertex is not at the origin. It all depends on the information provided.
When the vertex of the function and another point it intersects are known, use the standard form. In fact, the |x|-coordinate of the vertex corresponds to the parameter |h,| and the |y|-coordinate corresponds to parameter |k.|
||f(x)=a(x-h)^2+k|| where
|(h,k)|: coordinates of the vertex
Here's how to find the rule.
-
Replace |h| and |k| in the equation with the coordinates of the vertex.
-
Replace |x| and |f(x)| in the equation with the coordinates of a point other than the vertex.
-
Isolate parameter |a.|
-
Give the rule.
Find the rule of the quadratic function with a vertex at coordinates |(4,6)| that passes through point |(2,-2).|
-
Replace |h| and |k| in the equation with the vertex’s coordinates
||\begin{align}f(x)&=a(x-h)^2+k\\ f(x)&=a(x-\color{#fa7921}4)^2+\color{#3b87cd}6\end{align}|| -
Replace |x| and |f(x)| in the equation with the coordinates of a point other than the vertex
||\begin{align}f(x)&=a(x-4)^2+6\\ \color{#3a9a38}{-2}&=a(\color{#3a9a38}2-4)^2+6\end{align}|| -
Isolate parameter |a|
||\begin{align}-2&=a(2-4)^2+6\\ -2&=a(-2)^2+6\\ -2&=4a+6\\ -8&=4a\\ -2&=a\end{align}|| -
Give the rule
The function rule is |f(x)=-2(x-4)^2+6.|
Find the rule of the quadratic function with a vertex at the coordinates |(-1,2)| that passes through the point |(3,26).|
-
Replace |h| and |k| in the equation with the vertex’s coordinates
||\begin{align}f(x)&=a(x-h)^2+k\\ f(x)&=a(x-\color{#fa7921}{-1})^2+\color{#3b87cd}2\end{align}|| -
Replace |x| and |f(x)| in the equation with the coordinates of a point other than the vertex
||\begin{align}f(x)&=a(x+1)^2+2\\ \color{#3a9a38}{26}&=a(\color{#3a9a38}3+1)^2+2\end{align}|| -
Isolate parameter |a|
||\begin{align}26&=a(3+1)^2+2\\ 26&=a(4)^2+2\\ 26&=16a+2\\ 24&=16a\\ 1.5&=a\end{align}|| -
Give the rule
The function rule is |f(x)=1.5(x+1)^2+2.|
When the 2 zeros of the function and another point it intersects are known, use the factored form. The zeros correspond to parameters |x_1| and |x_2| in the rule.
||f(x)=a(x-x_1)(x-x_2)|| where
|x_1| and |x_2|: zeros (|x|-intercepts)
Here's how to find the rule.
-
Replace |x_1| and |x_2| in the equation with the zeros.
-
Replace |x| and |f(x)| in the equation with the coordinates of a point other than the zeros.
-
Isolate parameter |a.|
-
Give the rule.
The order in which |x_1| and |x_2| are placed in the rule does not matter.
Find the rule of the quadratic function with zeros that are |-3| and |8|, that passes through the point |(5,-24).|
-
Replace |x_1| and |x_2| in the equation with the zeros
||\begin{align}f(x)&=a(x-x_1)(x-x_2)\\f(x)&=a(x-\color{#ff55c3}{-3})(x-\color{#ff55c3}8)\end{align}|| -
Replace |x| and |f(x)| in the equation with the coordinates of a point other than the zeros
||\begin{align}f(x)&=a(x+3)(x-8)\\\color{#3a9a38}{-24}&=a(\color{#3a9a38}5+3)(\color{#3a9a38}5-8)\end{align}|| -
Isolate parameter |a|
||\begin{align}-24&=a(5+3)(5-8)\\-24&=a(8)(-3)\\ -24&=-24a\\1&=a\end{align}|| -
Give the rule
The function rule is |f(x)=(x+3)(x-8).|
Find the rule in general form of the quadratic function intersecting points |(-2,0),| |(7,18)| and |(3,0).|
It is not possible to directly determine the rule in the general form with the zeros, so we first find the rule in the factored form and then transform it.
-
Replace |x_1| and |x_2| in the equation with the zeros
Use points |(-2,0)| and |(3,0)| to determine the zeros of the function, which are are |-2| and |3.|
||\begin{align}f(x)&=a(x-x_1)(x-x_2)\\f(x)&=a(x-\color{#ff55c3}{-2 })(x-\color{#ff55c3}3)\end{align}|| -
Replace |x| and |f(x)| in the equation with the coordinates of a point other than the zeros
||\begin{align}f(x)&=a(x+2)(x-3)\\\color{#3a9a38}{18}&=a(\color{#3a9a38}7+2)(\color{#3a9a38}7-3 )\end{align}|| -
Isolate parameter |a|
||\begin{align}18&=a(7+2)(7-3)\\18&=a(9)(4)\\18&=36a\\0.5&=a\end{align} || -
Give the rule
The function rule in factored form is |f(x)=0.5(x+2)(x-3).|
Expand the expression to transform it into general form.
||\begin{align}f(x)&=0.5(x+2)(x-3)\\&= 0.5(x^2-3x+2x-6)\\&= 0.5(x^2-x-6)\\&= 0.5x^2-0.5x-3 \end{align}||
The rule of the function in general form is |f(x)=0.5x^2-0.5x-3.|
When we know 2 points of the function with the same |y|-value, it is possible to find the rule in standard form |\left(f(x)=a(x-h)^2+k\right).|
The parabola has a vertical axis of symmetry intersecting its vertex. Therefore, 2 points that have the same |y|-value are at equal distance from the axis of symmetry |x=h.| So, the |x|-coordinates of the points can be averaged to find the value of |h.|
||h=\dfrac{x_A+x_B}{2}|| where
|x_A| and |x_B|: |x|-values of the 2 points having the same |y|-value

Case 1: When the |\boldsymbol{y}|-coordinate at the vertex is known
-
Use the formula to calculate the value of |h|.
-
Check if the third point provided has an |x|-coordinate equal to |h.| If yes, the point is the vertex. If not, refer to case 2.
-
Replace |h| and |k| in the standard equation with the vertex coordinates.
-
Replace |x| and |f(x)| in the equation with the coordinates of a point different from the vertex.
-
Isolate |a.|
-
Give the rule.
Find the equation of the quadratic function represented in the table of values below.
| |x| | |-4| | |-3| | |-1| | |0| | |2| |
|---|---|---|---|---|---|
| |y| | |4| | |-1| | |-5| | |-4| | |4| |
-
Calculate the value of |h|
Points |(-4,4)| and |(2,4)| have the same |y|-coordinate, so we can calculate |h| from their |x|-coordinate.
||\begin{align}\color{#fa7921}h&=\dfrac{x_A+x_B}{2}\\ &=\dfrac{-4+2}{2}\\&=\dfrac{-2}{2}\\ &=\color{#fa7921}{-1}\end{align}|| -
Check if another point has an |x|-coordinate equal to |h|
We notice that |-1| is the |x|-coordinate of one of the points in the table of values. We determine that |(-1,5)| is the vertex of the parabola, so |\color{#3b87cd}k=\color{#3b87cd}{-5}.| -
Replace |h| and |k| in the equation with the coordinates of the vertex
||\begin{align}f(x)&=a(x-h)^2+k\\ f(x)&=a(x-\color{#fa7921}{-1})^2+\color{#3b87cd}{-5}\end{align}|| -
Replace |x| and |f(x)| in the equation with the coordinates of a point other than the vertex
We can use the point |(-4,4).|||\begin{align}f(x)&=a(x+1)^2-5 \\ \color{#3a9a38}{4}&=a(\color{#3a9a38}{-4}+1)^2-5\end{align}|| -
Isolate |a|
||\begin{align}4&=a(-3)^2-5\\4&=9a-5\\9&=9a\\1&=a\end{align}|| -
Give the rule
The rule of the function is |f(x)=(x+1)^2-5.|
Case 2: When the |\boldsymbol{y}|-coordinate of the vertex is unknown
In this case, there are 2 variables, parameters |a| and |k.| Therefore, it is necessary to create a system of equations and solve it.
-
Calculate the value of |h| using the formula.
-
Replace |h| in the equation with the value found in the previous step.
-
Create a system of equations by replacing |x| and |f(x)| with the coordinates of 2 points. The 2 points must not be the ones that have the same |y|-value.
-
Solve the system of equations to find the value of |a| and |k.|
-
Give the rule.
Find the equation of the following quadratic function.
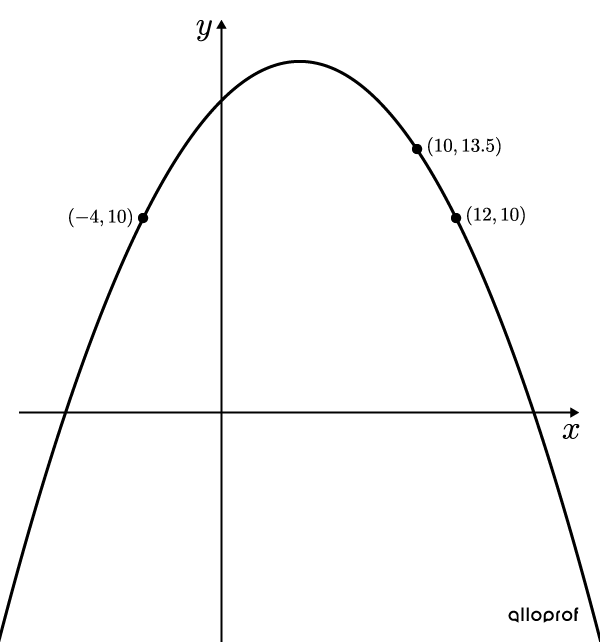
-
Calculate the value of |h|
||\begin{align}\color{#fa7921}h&=\dfrac{x_A+x_B}{2}\\ &=\dfrac{-4+12}{2}\\&=\dfrac{8}{2}\\ &=\color{#fa7921}4\end{align}|| -
Replace |h| in the equation
||\begin{align}f(x)&= a(x-h)^2+k\\ &=a(x-\color{#fa7921}{4})^2+k \end{align}|| -
Create a system of equations with 2 points
Equation 1
||\begin{align} \color{#3a9a38}{f(x)}&=a(\color{#3a9a38}{x}-4)^2+k\\ \color{#3a9a38}{10}&=a(\color{#3a9a38}{-4}-4)^2+k\\ 10&=a(-8)^2+k\\ 10&=64a+k\end{align}||
Equation 2
||\begin{align}\color{#3a9a38}{f(x)}&=a(\color{#3a9a38}{x}-4)^2+k\\\color{#3a9a38}{13.5}&=a(\color{#3a9a38}{10}-4)^2+k\\13.5&=a(6)^2+k\\13.5&=36a+k\end{align}||
-
Solve the system of equations to determine the value of |a| and |k|
Start by isolating |k| in the first equation to use the substitution method.
||\begin{align}10&=64a+k\\\color{#3b87cd}{10-64a}&=\color{#3b87cd}k\end{align}||
Then, replace |k| in the second equation with the found expression.
||\begin{align}13.5&=36a+\color{#3b87cd}k\\13.5&=36a+ \color{#3b87cd}{10-64a}\\13.5&=-28a+10\\3.5&=-28a\\\color{#3a9a38}{-0.125}&=\color{#3a9a38}a\end{align}||
Last, determine the value of |k.| Use the equation where |k| is isolated.
||\begin{align}k&=10-64\color{#3a9a38}{a}\\&=10-64(\color{#3a9a38}{-0.125})\\&=10--8\\&=18\end{align}|| -
Give the rule
The function rule is |f(x)=-0.125(x-4)^2+18.|