On appelle zéro, ou abscisse à l'origine d'une fonction |f,| une valeur de |x| pour laquelle |f(x)=0.| Une fonction peut avoir plusieurs zéros.
Trouver les zéros d'une fonction polynomiale de degré 2 revient à trouver le ou les points d'intersection entre la parabole et l'axe des |x.| Il peut y en avoir 1, 2 ou n’y en avoir aucun.
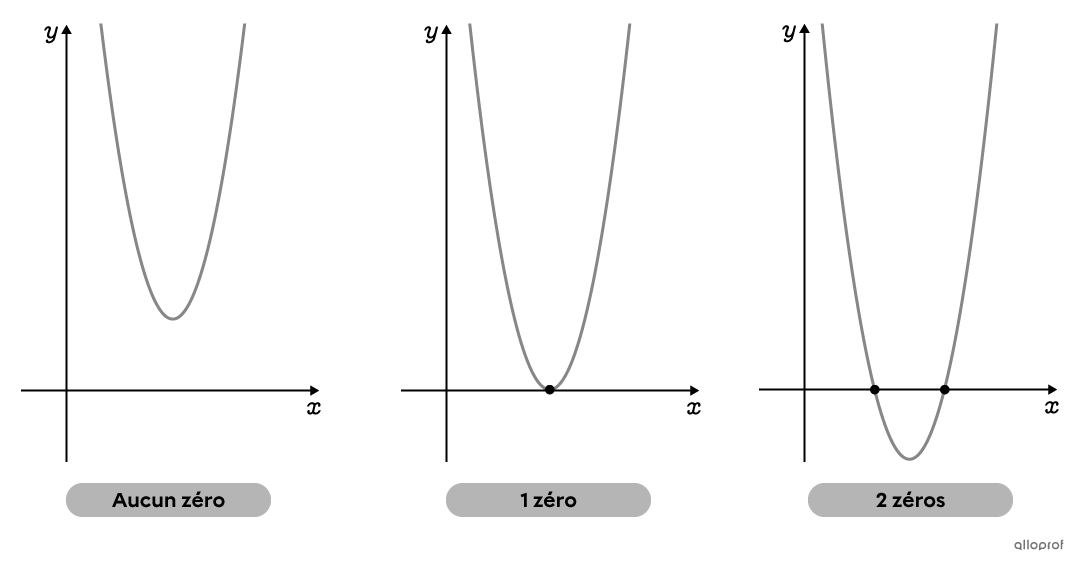
Trouver les zéros d'une fonction polynomiale de degré 2 sous la forme générale en utilisant les méthodes suivantes.
Trouver les zéros d'une fonction polynomiale de degré 2 sous la forme canonique en utilisant les méthodes suivantes.
Trouver les zéros d'une fonction polynomiale de degré 2 sous la forme factorisée en utilisant les méthodes suivantes.
Pour trouver le ou les zéros d’une fonction polynomiale de degré 2 sous la forme générale |f(x)=ax^2+bx+c,| il faut remplacer |f(x)| par |0,| puis trouver la ou les valeurs de |x| qui rendent l’équation vraie. Pour y arriver, on peut utiliser la factorisation ou la formule quadratique.
On ne peut pas isoler directement |x| dans l’équation |0=ax^2+bx+c| puisque la variable |x| se retrouve dans 2 termes qui ne sont pas semblables.
Lorsqu'on utilise la factorisation pour déterminer les zéros d'une fonction polynomiale de degré 2, il faut appliquer la règle du produit nul.
La règle du produit nul est la suivante.
Un produit de facteurs est nul si et seulement si au moins un de ses facteurs est nul.||a \times b = 0\\ \Updownarrow\\a=0\ \ \text{ou}\ \ b=0||
-
Remplacer |f(x)| par |0.|
-
Factoriser le polynôme.
-
Appliquer la règle du produit nul.
Voici un exemple où on détermine les zéros à l’aide d’un trinôme carré parfait.
Détermine les zéros de la fonction |f(x)=4x^2+12x+9.|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=4x^2+12x+9\\0&=4x^2+12x+9\end{align}|| -
Factoriser le polynôme
Ce polynôme est un trinôme carré parfait. Ainsi, on obtient l’équation suivante.||\begin{align} 0&=4x^2+12x+9\\ &=(2x+3)^2\end{align}||On a donc |0=(2x+3)^2| ou |0=(2x+3)(2x+3).| -
Appliquer la règle du produit nul
Comme les 2 facteurs sont identiques, on peut conclure que la fonction possède un seul zéro.||\begin{align}2x+3&=0\qquad\\ 2x&=-3\\x&=-\dfrac{3}{2}\end{align}||
Réponse : Le zéro de la fonction est |-\dfrac{3}{2}.|
Voici un exemple où on détermine les zéros à l’aide de la complétion du carré.
Détermine les zéros de la fonction |f(x)=x^2-0{,}8x-3{,}84.|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=x^2-0{,}8x-3{,}84\\0&=x^2-0{,}8x-3{,}84\end{align}|| -
Factoriser le polynôme
||\begin{align}&x^2-0{,}8x-3{,}84\\=\ &(x^2-0{,}8x\color{#3a9a38}{+0{,}16})-3{,}84\color{#3a9a38}{-0{,}16}\\=\ &(x-0{,}4)^2-4\\=\ &\big((x-0{,}4)+2\big)\big((x-0{,}4)-2 \big)\\=\ &(x+1{,}6)(x-2{,}4) \end{align}||
On a donc |0=(x+1{,}6)(x-2{,}4).|
-
Appliquer la règle du produit nul
||\begin{aligned}x+1{,}6&=0\\ x_1&=-1{,}6\end{aligned}\qquad \begin{aligned}x-2{,}4&=0\\ x_2&=2{,}4\end{aligned}||
Réponse : Les 2 zéros de la fonction sont |-1{,}6| et |2{,}4.|
Voici un exemple où on détermine les zéros à l’aide de la technique du produit-somme.
Détermine les zéros de la fonction |f(x)=x^2-3x-10.|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=x^2-3x-10\\0&=x^2-3x-10\end{align}|| -
Factoriser le polynôme
Ce polynôme se factorise avec la technique du produit-somme. On cherche 2 nombres |m| et |n| dont le produit |m \times n| doit être égal à |-10| et dont la somme |m+n| doit être égale à |-3.| En regardant les différents facteurs de |-10,| on obtient |\color{#3b87cd}m=\color{#3b87cd}{-5}| et |\color{#3b87cd}n=\color{#3b87cd}{2}.| On peut maintenant effectuer la factorisation.||\begin{align}&x^2-3x-10\\ =\ &x^2\color{#3b87cd}{-5}x+\color{#3b87cd}2x-10 \\=\ &x(x-5) + 2(x-5)\\=\ & (x-5)(x+2)\end{align}||On a donc |0=(x-5)(x+2).| -
Appliquer la règle du produit nul
On vérifie pour quelles valeurs de |x| chacun des facteurs vaut |0.|||\begin{aligned}x-5&=0\\ x_1&=5\end{aligned}\qquad \begin{aligned}x+2&=0\\ x_2&=-2\end{aligned}||
Réponse : Les 2 zéros de la fonction sont |-2| et |5.|
Il est aussi possible d’utiliser la formule quadratique lorsque la fonction est donnée sous la forme générale. Voici comment procéder.
-
Remplacer |f(x)| par |0.|
-
Déterminer la valeur de |a,| |b| et |c.|
-
Appliquer la formule quadratique.
Voici un des exemples qui a été résolu avec la factorisation précédemment, mais cette fois, en utilisant la formule quadratique.
Déterminer les zéros de la fonction |f(x)=x^2-3x-10.|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=x^2-3x-10\\0&=\color{#ec0000}1x^2\color{#3b87cd}{-3}x\color{#3a9a38}{-10}\end{align}|| -
Déterminer la valeur de |a,| |b| et |c|
||\color{#ec0000}a=\color{#ec0000}1,\ \color{#3b87cd}b=\color{#3b87cd}{-3}, \ \color{#3a9a38}c=\color{#3a9a38}{-10}|| -
Appliquer la formule quadratique
||\begin{align}x_{1,2} &= \dfrac{-\color{#3b87cd}b \pm \sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\\\ &= \dfrac{-(\color{#3b87cd}{-3}) \pm \sqrt{(\color{#3b87cd}{-3})^2-4(\color{#ec0000}1)(\color{#3a9a38}{-10})}}{2(\color{#ec0000}1)} \\ &= \dfrac{3 \pm \sqrt{9 + 40}}{2}\\ &= \dfrac{3 \pm \sqrt{49}}{2}\\&= \dfrac{3 \pm 7}{2} \end{align}||À cette étape, on sépare la formule en 2 parties, une utilisant le |+| et l'autre utilisant le |-.| ||\begin{aligned} x_1 &= \dfrac{3 + 7}{2}\\&=5 \end{aligned}\qquad\begin{aligned}x_2 &= \dfrac{3 - 7}{2}\\&=-2\end{aligned}||
Réponse : Les 2 zéros de la fonction sont |-2| et |5.| C’est la même réponse qu’on a obtenue à l’aide de la factorisation précédemment.
Voici un exemple où les zéros ne sont pas des nombres entiers.
Détermine les zéros de la fonction |f(x)=2x^2+3x-4.|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=2x^2+3x-4\\0&=2x^2+3x-4\end{align}|| -
Déterminer la valeur de |a,| |b| et |c|
||a=2,\ b=3,\ c=-4|| -
Appliquer la formule quadratique
||\begin{align}x_{1,2} &= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\\\ &= \dfrac{-3 \pm \sqrt{3^2-4(2)(-4)}}{2(2)} \\ &= \dfrac{-3 \pm \sqrt{9+32}}{4}\\ &= \dfrac{-3 \pm \sqrt{41}}{4}\end{align}||À cette étape, il faut extraire la racine carrée de |41.| Comme ce n’est pas un nombre carré, on sépare tout de suite la formule en 2 parties, l'une utilisant le |+| et l'autre utilisant le |-.| ||\begin{aligned} x_1 &=\dfrac{-3 + \sqrt{41}}{4}\\&\approx0{,}85 \end{aligned}\qquad\begin{aligned}x_2 &=\dfrac{-3 - \sqrt{41}}{4}\\&\approx -2{,}35\end{aligned}||
Réponse : Les zéros sont |\approx 0{,}85| et |\approx -2{,}35.| Pour avoir une réponse plus précise, on peut conserver la racine. ||\begin{align}x_1 &= \dfrac{-3 + \sqrt{41}}{4}\\ x_2&=\dfrac{-3 - \sqrt{41}}{4}\end{align}||
Voici un exemple où la fonction n’a pas de zéro.
Détermine les zéros de la fonction |f(x)=-6x^2+2x-3.|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=-6x^2+2x-3\\0&=-6x^2+2x-3\end{align}|| -
Déterminer la valeur de |a,| |b| et |c|
||a=-6,\ b=2,\ c=-3|| -
Appliquer la formule quadratique
||\begin{align}x_{1,2} &= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\\\ &= \dfrac{-2 \pm \sqrt{(2)^2-4(-6)(-3)}}{2(-6)} \\ &= \dfrac{-2 \pm \sqrt{4-72}}{-12}\\ &= \dfrac{-2 \pm \sqrt{\color{#EC0000}{-68}}}{-12} \end{align}||On ne peut pas continuer la résolution puisque le nombre sous la racine carrée est négatif. On en conclut que cette fonction n’a pas de zéro.
Réponse : La fonction n’a pas de zéro.
Il est possible de déterminer le nombre de zéros que possède une fonction polynomiale de degré 2 en analysant le discriminant dans la formule quadratique.
-
Si |b^2-4ac>0,| la fonction a 2 zéros.
-
Si |b^2-4ac=0,| la fonction a 1 seul zéro.
-
Si |b^2-4ac<0,| la fonction n’a pas de zéro.
Pour trouver les zéros d’une fonction polynomiale de degré 2 sous la forme canonique |f(x)=a(x-h)^2+k,| il faut remplacer |f(x)| par |0| puis trouver la ou les valeurs de |x| qui rendent l’équation vraie. On peut isoler |x| directement dans l’équation ou bien utiliser la formule des zéros pour la forme canonique.
Lorsque la règle d’une fonction polynomiale de degré 2 est sous la forme canonique, il est possible de simplement résoudre l’équation pour trouver le ou les zéro. Voici comment procéder.
-
Remplacer |f(x)| par |0.|
-
Isoler les parenthèses.
-
Extraire la racine carrée des 2 côtés de l’égalité.
-
Résoudre les équations.
Lorsqu’on extrait la racine carrée d’un nombre, il y a 2 réponses : une positive et une négative.
Détermine les zéros de la fonction |f(x)=-3(x+5)^2+12.|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=-3(x+5)^2+12\\ 0&=-3(x+5)^2+12\end{align}|| -
Isoler les parenthèses
||\begin{align}-12&=-3(x+5)^2\\4&=(x+5)^2\end{align}|| -
Extraire la racine carrée
||\begin{align}\color{#ec0000}{\sqrt{\color{black}4}}&=\color{#ec0000}{\sqrt{\color{black}{(x+5)^2}}}\\ \pm\ 2&=x+5\end{align}|| -
Résoudre les équations
||\begin{aligned}-2&=x+5\\-7&=x_1 \end{aligned} \qquad \begin{aligned} 2&=x+5\\-3&=x_2\end{aligned}||
Réponse : Les 2 zéros de la fonction sont |-7| et |-3.|
Voici un exemple où la fonction n’a pas de zéro.
Détermine les zéros de la fonction |f(x)=2(x-1)^2+6.|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=2(x-1)^2+6\\ 0&=2(x-1)^2+6\end{align}|| -
Isoler les parenthèses
||\begin{align}-6&=2(x-1)^2\\-3&=(x-1)^2\end{align}|| -
Extraire la racine carrée
||\begin{align}\color{#ec0000}{\sqrt{\color{black}{-3}}}&=\color{#ec0000}{\sqrt{\color{black}{(x-1)^2}}}\end{align}||Il est impossible d’extraire la racine carrée d’un nombre négatif. On arrête donc la résolution et on conclut que cette fonction n’a pas de zéro.
Réponse : La fonction n’a pas de zéro.
Il est possible de déterminer le nombre de zéros qu’aura une fonction polynomiale de degré 2 sous la forme canonique en analysant les paramètres |a| et |k.| Le signe du paramètre |a| indique le sens de l’ouverture de la parabole (vers le haut ou vers le bas), tandis que le paramètre |k| indique l’emplacement vertical du sommet.
Dans l’exemple précédent, puisque |a>0| et |k>0,| la fonction n’a pas de zéro.
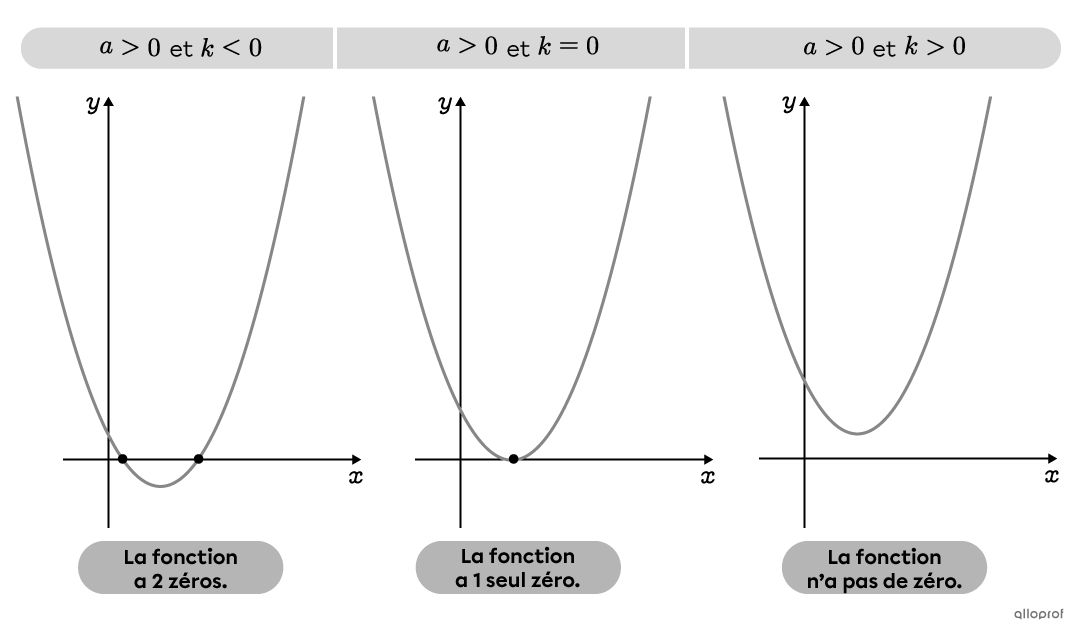
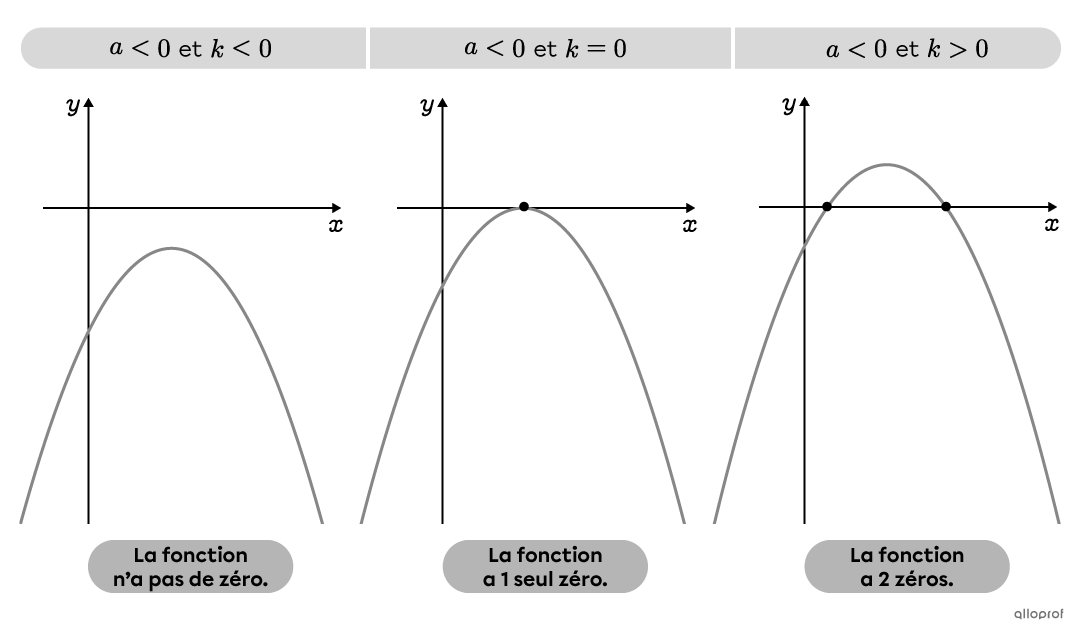
Il est aussi possible d’utiliser la formule des zéros lorsque la fonction est donnée sous la forme canonique.
La formule pour trouver les zéros d'une fonction polynomiale de degré 2 sous la forme canonique est la suivante.||x_{1,2}= h \pm \sqrt{-\dfrac{k}{a}}||
Voici la démonstration de la formule des zéros sous la forme canonique.
On doit isoler |x| dans l’équation |a(x-h)^2+k=0| en faisant toutes les opérations inverses.||\begin{align}a(x-h)^2+k&=0\\
a(x-h)^2+k\color{#ec0000}{-k}&=0\color{#ec0000}{-k}\\
\color{#ec0000}{\dfrac{\color{black}{a(x-h)^2}}{a}}&=\color{#ec0000}{\dfrac{\color{black}{-k}}{a}}\\
\color{#ec0000}{\sqrt{\color{black}{(x-h)^2}}}&=\color{#ec0000}{\pm \sqrt{\color{black}{-\dfrac{k}{a}}}}\\
x-h \color{#ec0000}{+h}&=\pm \sqrt{\color{black}{-\dfrac{k}{a}}}\color{#ec0000}{+h}\\
x&=h \pm \sqrt{-\dfrac{k}{a}}\end{align}||On obtient bel et bien la formule des zéros.
Les étapes de résolution pour déterminer la formule sont les mêmes que lorsqu’on utilise la technique par résolution d’équation. C’est pourquoi les 2 façons de faire sont parfaitement équivalentes.
-
Remplacer |f(x)| par |0.|
-
Déterminer la valeur des paramètres |a,| |h| et |k.|
-
Appliquer la formule des zéros.
Détermine les zéros de la fonction |f(x)=2(x+1)^2-8.|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=2(x+1)^2-8\\ 0&=2(x+1)^2-8\end{align}|| -
Déterminer la valeur des paramètres |a,| |h| et |k|
||a=2,\ h=-1,\ k=-8|| -
Appliquer la formule des zéros
||\begin{align}x_{1,2}&= h \pm\sqrt{-\dfrac{k}{a}}\\ &= -1 \pm \sqrt{-\dfrac{-8}{2}}\\&= -1 \pm \sqrt{4}\\&= -1 \pm 2\end{align}||À cette étape, on sépare la formule en 2 parties, l'une utilisant le |+| et l'autre utilisant le |-.|
||\begin{aligned}x_1&=-1-2\qquad \\&=-3\end{aligned}\begin{aligned}x_2&=-1+2\\&=1\end{aligned}||
Réponse : Les 2 zéros de la fonction sont |-3| et |1.|
Il est possible de déterminer le nombre de zéros que possède une fonction polynomiale de degré 2 en analysant le radicande (l’expression qui se trouve sous la racine) dans la formule des zéros.
-
Si |- \dfrac{k}{a} >0,| la fonction a 2 zéros.
-
Si |- \dfrac{k}{a} =0,| la fonction a 1 seul zéro.
-
Si |- \dfrac{k}{a} <0,| la fonction n’a pas de zéro.
Pour trouver les zéros d’une fonction polynomiale de degré 2 sous la forme factorisée |f(x)=a(x-x_1)(x-x_2),| il suffit de déterminer la valeur de |x_1| et |x_2| à l’aide de la règle. L’avantage de cette forme d’écriture est qu’elle donne directement la valeur des zéros.
Trouve les zéros de la fonction |f(x)=-0{,}5(x+2{,}7)(x-6{,}2).|
Il faut déterminer |x_1| et |x_2.| Comme il y a des soustractions à l’intérieur des parenthèses dans le modèle de la forme factorisée, il faut s’assurer de les retrouver aussi dans notre règle.||\begin{align} f(x) &= -0{,}5(x+2{,}7)(x-6{,}2) \\ f(x) &= -0{,}5\big(x-(\color{#3a9a38}{-2{,}7})\big)\big(x-\color{#3a9a38}{6{,}2}\big) \end{align}||
Réponse : Les 2 zéros de la fonction sont |-2{,}7| et |6{,}2.|
On peut aussi appliquer la même méthode que lorsqu’on a la règle en forme générale. Voici un exemple identique à l’exemple précédent, résolu cette fois en utilisant la règle du produit nul.
Trouve les zéros de la fonction |f(x)=-0{,}5(x+2{,}7)(x-6{,}2).|
-
Remplacer |f(x)| par |0|
||\begin{align}f(x)&=-0{,}5(x+2{,}7)(x-6{,}2) \\ 0&=-0{,}5(x+2{,}7)(x-6{,}2)\end{align}||
-
Factoriser le polynôme
Le polynôme est déjà factorisé. -
Appliquer la règle du produit nul
On vérifie pour quelles valeurs de |x| chacun des facteurs vaut |0.| Comme le facteur |-0{,}5| ne contient pas la variable |x,| on n’en tient pas compte.
||\begin{aligned}x+2{,}7&=0\\ x_1&=-2{,}7\end{aligned}\qquad\!\! \begin{aligned}x-6{,}2&=0\\ x_2&=6{,}2\end{aligned}||
Réponse : Les zéros de la fonction sont bel et bien |-2{,}7| et |6{,}2.|