Selon la forme d'équation dont on dispose, on procède différemment pour tracer une droite dans un plan cartésien.
Une méthodologie relative à chaque forme d'équation est présentée ci-dessous. Toutefois, peu importe la forme d'équation considérée, il est toujours possible de tracer une droite grâce à une table de valeurs construite à partir de l'équation.
Tracer une fonction affine
Il arrive parfois qu'on ne connaisse pas l'équation de la droite. On peut tout de même représenter celle-ci si les coordonnées d'un point et la valeur de la pente (paramètre |a|) nous sont fournies. Dans ce cas, on peut tracer une droite en suivant les étapes suivantes.
-
On place le point donné à l'aide de ses coordonnées dans le plan cartésien.
-
À l'aide de la valeur de la pente, on place d'autres points à l'aide de la méthode de l'escalier (le numérateur de la pente représente le déplacement vertical alors que le dénominateur de la pente représente le déplacement horizontal).
-
On trace la droite qui passe par ces points.
Si la pente fournie est un nombre entier, il suffit de considérer ce nombre comme le numérateur d'une fraction dont le dénominateur est 1.
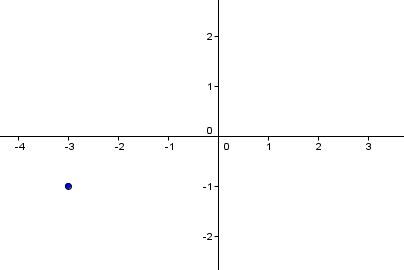
Tracer une droite passant par le point |(-3,-1)| et dont la pente est |\dfrac{1}{2}.|
-
On place le point donné.
-
On place d'autres points à l'aide de la valeur de la pente.
La pente est de |\dfrac{1}{2},| ce qui indique qu'on se déplace de |2| unités vers la droite |(x)| et de |1| unité vers le haut |(y).|
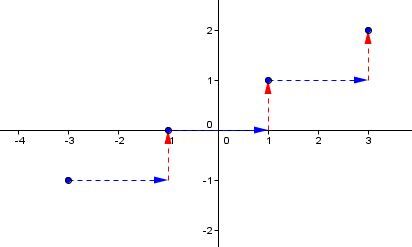
-
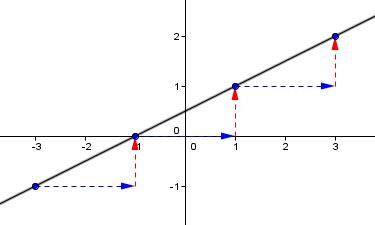
On trace la droite qui passe par les nouveaux points placés.
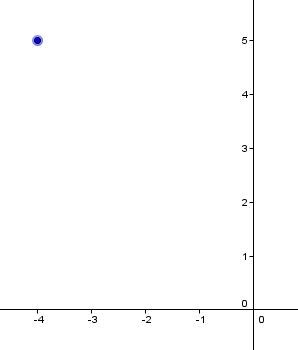
Tracer une droite passant par le point |(-4,5)| et dont la pente vaut |-2.|
-
On place le point |\boldsymbol{(-4, 5).}|
-
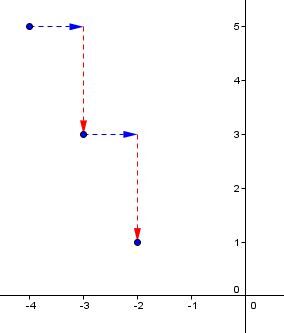
On place d'autres points à l'aide de la valeur de la pente.
La pente indique que, chaque fois qu'on se déplace de |1| unité vers la droite |(x),| on se déplace de |2| unités vers le bas |(y).|
-
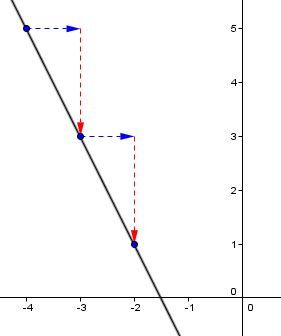
On trace la droite qui passe par les nouveaux points placés.
Si la valeur de la pente est inconnue mais que les coordonnées de deux points sont fournies, il suffit placer les deux points dans le plan cartésien et de les relier par une droite afin de tracer le graphique.
La forme fonctionnelle de l'équation d'une droite s'écrit sous la forme |y = ax + b.| On peut tracer une droite dont l'équation est écrite sous cette forme en suivant les étapes suivantes.
-
On place l'ordonnée à l'origine (qui correspond à la valeur du paramètre |b|) dans le plan cartésien.
-
À partir de l'ordonnée à l'origine, on place un autre point en utilisant la pente de la droite (qui correspond à la valeur du paramètre |a|).
-
On trace la droite qui passe par ces 2 points.
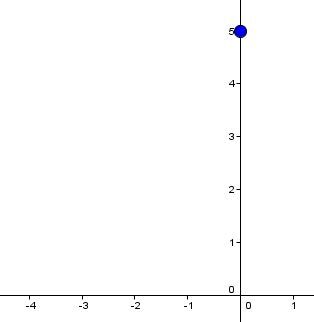
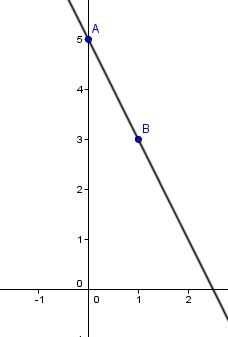
Soit l'équation |y = -2x + 5.|
-
On place l'ordonnée à l'origine |\boldsymbol{(b = 5)}| dans le plan cartésien.
-
À partir de ce point, on utilise la pente |\boldsymbol{(a = -2)}| afin d'en placer un second dans le plan cartésien.
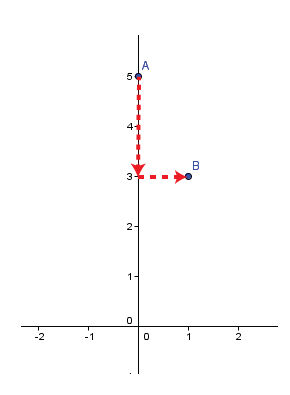
-
On trace la droite qui passe par ces 2 points.
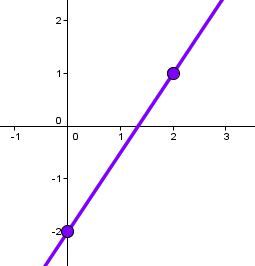
Soit l'équation |y = \dfrac{3}{2}x - 2.|
-
On place l'ordonnée à l'origine |\boldsymbol{(b = -2)}| dans le plan cartésien.
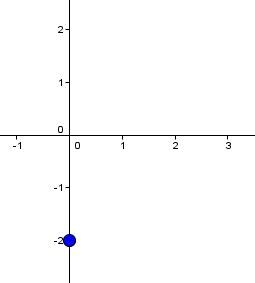
-
À partir de ce point, on utilise la pente |\boldsymbol{\left(a = \dfrac{3}{2}\right)}| afin d'en placer un second dans le plan cartésien.

-
On trace la droite qui passe par ces 2 points.
La forme symétrique de l'équation d'une droite s'écrit sous la forme de |\dfrac{x}{\text{a}} + \dfrac{y}{b} = 1.| On peut tracer une droite dont l'équation est écrite sous cette forme en suivant les étapes suivantes.
-
On place l'ordonnée à l'origine (qui correspond à la valeur du paramètre |b|) et l'abscisse à l'origine (qui correspond à la valeur du paramètre |\text{a}|) dans le plan cartésien.
-
On trace la droite qui passe par ces 2 points.
Soit l'équation |\dfrac{x}{3} + \dfrac{y}{9} = 1.|
-
Placer l’ordonnée à l’origine et l’abscisse à l’origine.
L'ordonnée à l'origine est égale à |\color{#333fb1}{b = 9}| et l'abscisse à l'origine est égale à |\color{#ec0000}{\text{a} = 3}.| On place ces 2 points dans le plan cartésien.
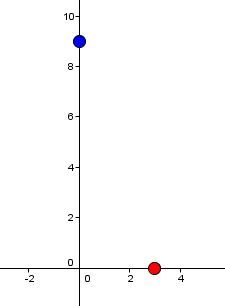
-
On trace la droite qui passe par ces 2 points.
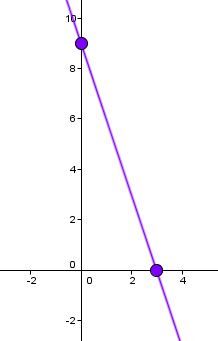
Soit l'équation |\dfrac{x}{5} - \dfrac{y}{2} = 1.|
-
Placer l’ordonnée à l’origine et l’abscisse à l’origine.
L'ordonnée à l'origine est égale à |\color{#333fb1}{b = -2}| et l'abscisse à l'origine est égale à |\color{#ec0000}{\text{a} = 5}.| On place ces 2 points dans le plan cartésien.

-
On trace la droite qui passe par ces 2 points.
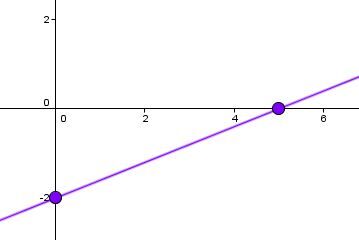
La forme générale de l'équation d'une droite s'écrit sous la forme de |Ax + By + C = 0.| On peut tracer une droite dont l'équation est écrite sous cette forme en suivant les étapes suivantes.
-
On détermine la valeur de l'ordonnée à l'origine de la droite en calculant la valeur de |y| lorsque |x=0.|
-
On détermine la valeur de l'abscisse à l'origine de la droite en calculant la valeur de |x| lorsque |y=0.|
-
On place ces 2 coordonnées dans le plan cartésien.
-
On trace la droite qui passe par ces 2 points.
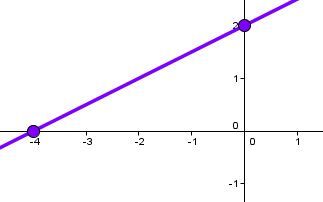
Soit l'équation |4x - 8y + 16 = 0.|
-
On détermine la valeur de l'ordonnée à l'origine.||\begin{align}4(0) - 8y + 16 &= 0\\-8y &= -16\\y &= 2\end{align}||
-
On détermine la valeur de l'abscisse à l'origine.||\begin{align}4x - 8(0) + 16 &= 0\\4x &= -16\\x &= -4\end{align}||
-
On place ces 2 coordonnées dans le plan cartésien.
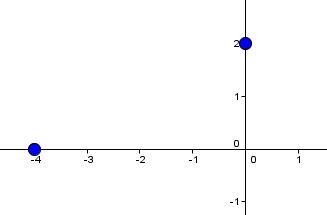
-
On trace la droite qui passe par ces 2 points.