Une fonction affine est représentée dans un plan cartésien par une droite. On la trace généralement de 2 façons : à l’aide d’une table de valeurs ou des paramètres |a| et |b.|
Lorsqu’on trace une fonction affine, il faut déterminer au moins 2 points qui lui appartiennent. Toutefois, il peut être bénéfique d’en trouver davantage pour avoir un tracé plus précis.
Pour tracer une fonction affine à partir d’une table de valeurs, on suit les étapes suivantes.
-
Créer la table de valeurs.
-
Placer les points dans un plan cartésien.
-
Tracer la droite.
Lorsqu’on construit une table de valeurs, on place les valeurs de |x| en ordre croissant. Par ailleurs, il n’est pas nécessaire d’avoir des bonds réguliers entre chaque valeur.
Trace la fonction affine dont la règle est |y=2x-4.|
-
Créer la table de valeurs
On choisit aléatoirement des valeurs que l'on veut donner à |x| et on détermine la valeur de |y| correspondante.
On utilise |x=1.| ||\begin{align}y&=2\color{#3B87CD}x-4\\y&=2(\color{#3B87CD}{1})-4\\y&=2-4\\y&=-2\end{align}|| Lorsque |x=1,| |y=-2.| Le premier couple est donc |(1,-2).|
On poursuit en choisissant une autre valeur de |x.| On utilise |x=0.|||\begin{align}y&=2\color{#3B87CD}x-4\\y&=2(\color{#3B87CD}{0})-4\\y&=0-4\\y&=-4\end{align}||Le deuxième couple est donc |(0,-4).|
| |x| | |y| |
|---|---|
| |-1| | |-6| |
| |0| | |-4| |
| |1| | |-2| |
| |3| | |2| |
On continue la construction de la table de valeurs de la même façon pour déterminer davantage de points. On obtient les points |(3,2)| et |(-1,-6).|
-
Placer les points dans un plan cartésien
On trace l’axe des |x| et l’axe des |y.| On effectue la graduation appropriée selon les points déterminés à l’étape précédente. Ici, une graduation de |1| unité fonctionne bien.

-
Tracer la droite
À l’aide d’une règle, on relie les points afin de tracer la droite représentant la fonction affine.
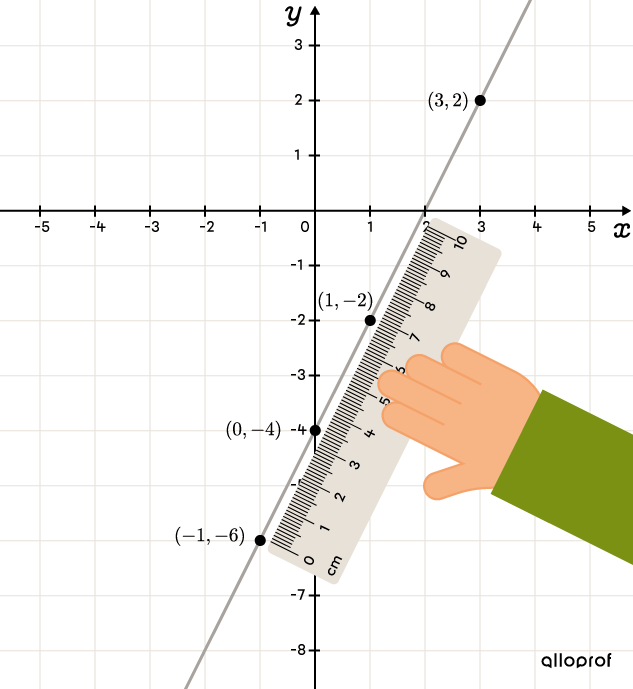
Afin de bien couvrir le plan cartésien, on choisit généralement des valeurs de |x| négatives et positives. De plus, choisir |x=0| est une bonne stratégie étant donné que la valeur déterminée correspond à l’ordonnée à l’origine, c’est-à-dire à l’endroit où la droite coupe l’axe des |y.|
Finalement, on doit prolonger la droite avant et après les points choisis puisqu’une fonction affine se prolonge à l’infini.
Il est possible de tracer le graphique d’une fonction affine en utilisant ses paramètres. En effet, le paramètre |a| correspond au taux de variation (qu’on appelle aussi la pente) et le paramètre |b| correspond à l’ordonnée à l’origine (aussi appelée la valeur initiale). Ces 2 informations sont suffisantes pour tracer la fonction. On procède de la façon suivante.
-
Placer l’ordonnée à l’origine |(b).|
-
Placer le ou les prochain(s) point(s) à l’aide du taux de variation |(a).| Pour ce faire, utiliser la formule du calcul de la pente.||a=\dfrac{\Delta y}{\Delta x}=\dfrac{\text{Variation en }y}{\text{Variation en }x}||
-
Tracer la droite.
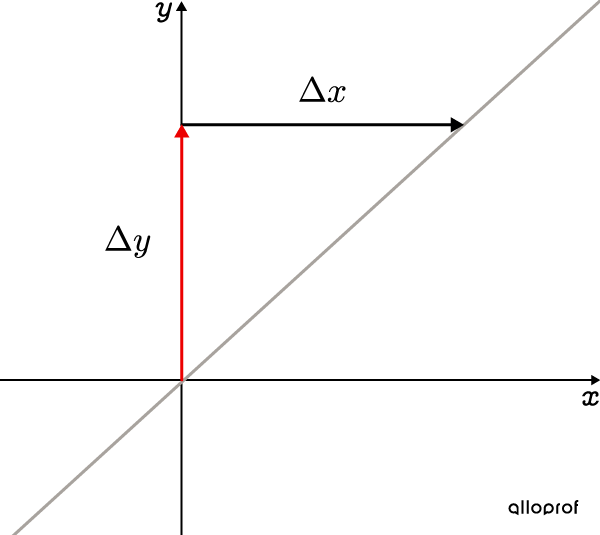
Lorsque le taux de variation est positif, on monte en |y| dans le plan cartésien. Le déplacement en |x| se fait vers la droite.||\color{#EC0000}+a=\dfrac{\color{#EC0000}+\Delta y}{\color{#EC0000}+\Delta x}||
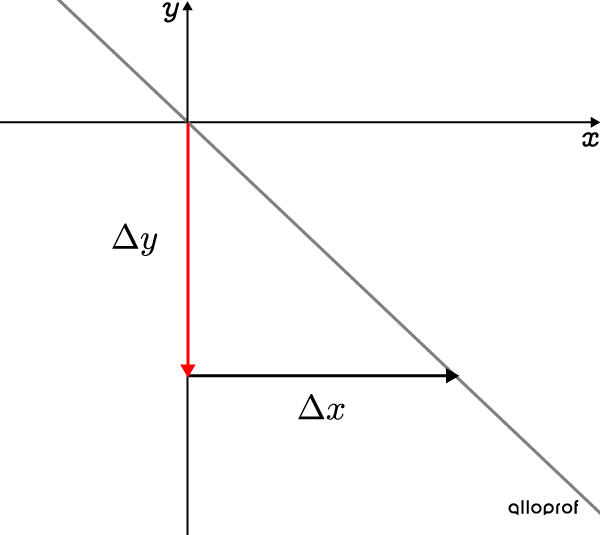
Lorsque le taux de variation est négatif, on descend en |y| dans le plan cartésien. Le déplacement en |x| se fait vers la droite.||\color{#EC0000}-a=\dfrac{\color{#EC0000}-\Delta y}{\color{#EC0000}+\Delta x}||
Trace la fonction affine dont la règle est |y=-\dfrac{3}{2}x+1.|
-
Placer l’ordonnée à l’origine |(b)|
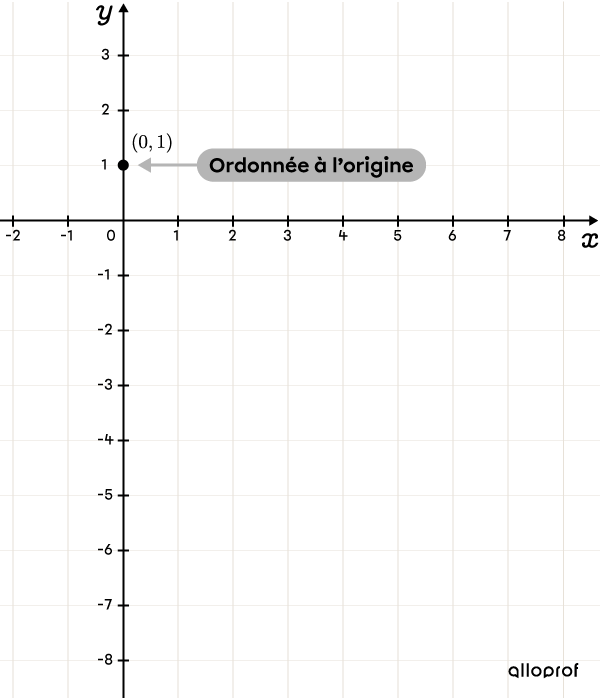
L’ordonnée à l’origine correspond au terme constant dans la règle.||\begin{align}y&=ax+\color{#3A9A38}b\\y&=-\dfrac{3}{2}x+\color{#3A9A38}1\end{align}||||\color{#3A9A38}b=\color{#3A9A38}1||L’ordonnée à l’origine se situe au point |(0,1).|
-
Placer les prochains points grâce au taux de variation
Le taux de variation correspond au coefficient de la variable |x| dans la règle.||\begin{align}y&=\color{#3B87CD}ax+b\\y&=\color{#3B87CD}{-\dfrac{3}{2}}x+1\\\\\color{#3B87CD}{a}&=\color{#3B87CD}{-\dfrac{3}{2}}\end{align}||
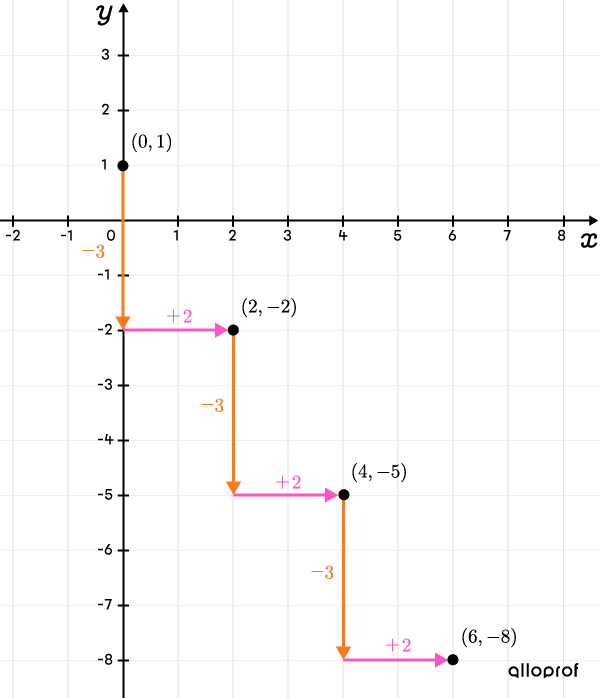
On utilise la formule de la pente.||\begin{align}a=\dfrac{\color{#FA7921}{-3}}{\color{#FF55C3}2}=\dfrac{\color{#FA7921}{\text{Variation en }y}}{\color{#FF55C3}{\text{Variation en }x}}\end{align}||À partir de l’ordonnée à l’origine, on doit descendre de |\color{#FA7921}3| unités, puis se déplacer de |\color{#FF55C3}2| unités vers la droite. On obtient le point |(2,-2).|
En répétant le même processus à partir du point |(2,-2),| on obtient les points |(4,-5)| et |(6,-8).|
-
Tracer la droite
À l’aide d’une règle, on relie les points afin de tracer la droite représentant la fonction affine.

Lorsque le taux de variation est écrit en notation décimale, il est judicieux de le transformer en notation fractionnaire. De plus, si |a| est négatif, alors le numérateur de la fraction est négatif.
Ex. :
Si |a=2{,}5,| on écrit |a=\dfrac{5}{2}.|
Si |a=4,| on écrit |a=\dfrac{4}{1}.|
Si |a=\color{#EC0000}{-}\dfrac{4}{3},| on écrit |a=\dfrac{\color{#EC0000}{-}4}{3}.|
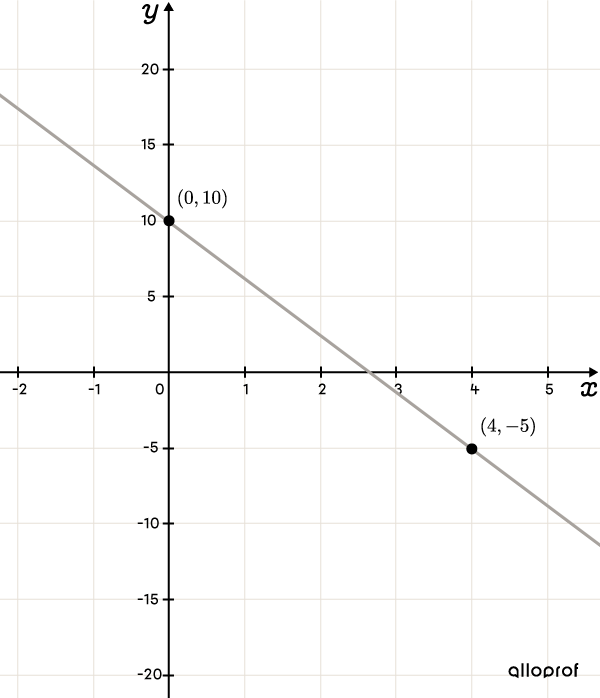
Trace la fonction affine dont la règle est |y=-3{,}75x+10.|
-
Placer l’ordonnée à l’origine |(b)|
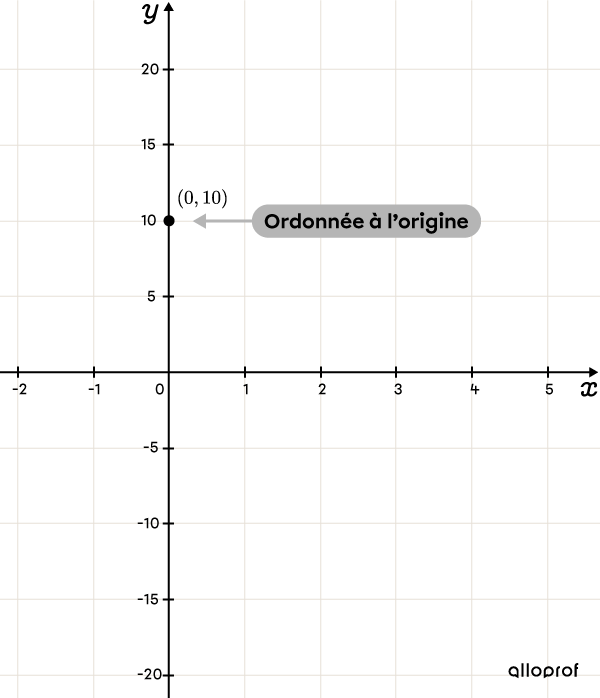
||\begin{align}y&=ax+\color{#3A9A38}b\\y&=-3{,}75x+\color{#3A9A38}{10}\end{align}||||\color{#3A9A38}b=\color{#3A9A38}{10}||L’ordonnée à l’origine se situe au point |(0,10).|
-
Placer les prochains points grâce au taux de variation||\begin{align}y&=\color{#3B87CD}ax+b\\y&=\color{#3B87CD}{3{,}75}x+10\end{align}||On transforme la notation décimale en notation fractionnaire.||\color{#3B87CD}{a}=\color{#3B87CD}{-3{,}75}=\color{#3B87CD}{\dfrac{-15}{4}}||
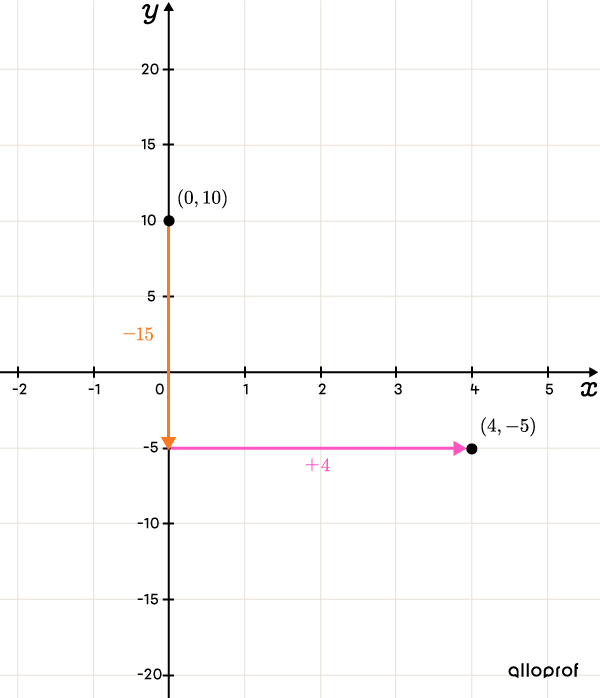
On utilise la formule de la pente.||\begin{align}a=\dfrac{\color{#FA7921}{-15}}{\color{#FF55C3}4}=\dfrac{\color{#FA7921}{\text{Variation en }y}}{\color{#FF55C3}{\text{Variation en }x}}\end{align}||À partir de l’ordonnée à l’origine, on doit descendre de |\color{#FA7921}{15}| unités, puis se déplacer de |\color{#FF55C3}{4}| unités vers la droite.
Lorsque le taux de variation indique une grande variation, il est nécessaire de changer la graduation. Ici, on peut faire des bonds de |5| unités en |y| et de |1| unité en |x.| De cette façon, on descend l’équivalent de |3| cases seulement. On obtient le point |(4,-5).|
-
Relier les points
À l’aide d’une règle, on relie les points afin de tracer la droite représentant la fonction affine.