Une équation ou une inéquation irrationnelle contient une variable sous une racine.
Il faut constamment tenir compte de 2 restrictions particulières lorsqu’on résout une équation ou une inéquation contenant une racine carrée.
-
La racine carrée est toujours supérieure ou égale à |0.|
||\sqrt{a}\ge0|| -
Le terme sous la racine carrée, appelé radicande, est toujours supérieur ou égal à |0.|
||a\ge0||
C’est en se référant aux restrictions qu’il est possible de valider les solutions obtenues lors de la résolution de l’équation ou de l’inéquation.
Voici la marche à suivre pour résoudre une équation comportant une ou des racines carrées.
-
Isoler la ou l’une des racine(s) carrée(s).
-
Vérifier si la racine carrée est supérieure ou égale à |0| et calculer la restriction, au besoin.
-
Élever au carré les 2 membres de l’équation.
-
Résoudre l’équation.
-
Valider la ou les solution(s).
-
Donner l'ensemble-solution.
Résous l'équation |4\sqrt{3x}=60.|
-
Isoler la racine carrée
||\begin{align}4\sqrt{3x}&=60\\\sqrt{3x}&=15\end{align}|| -
Calculer les restrictions
On remarque que |\sqrt{3x}| est supérieure à |0,| puisque c’est égal à |15.| Ceci implique qu’il existe au moins une solution. On trouve la restriction pour que le terme sous la racine soit positif.||\begin{align}3x&\ge0\\x&\ge0\end{align}|| -
Élever au carré les 2 membres de l’équation
||\begin{align}\sqrt{3x}&=15\\\color{#EC0000}{(\color{black}{\sqrt{3x}})^2}&=15^{\color{#EC0000}{2}}\end{align}|| -
Résoudre l’équation
||\begin{align}3x&=225\\\color{#3A9A38}{x}&=\color{#3A9A38}{75}\end{align}|| -
Valider la solution
La restriction |x\ge0| calculée à l’étape 2 est respectée, car |\color{#3A9A38}{75}\ge0.| -
Donner la solution
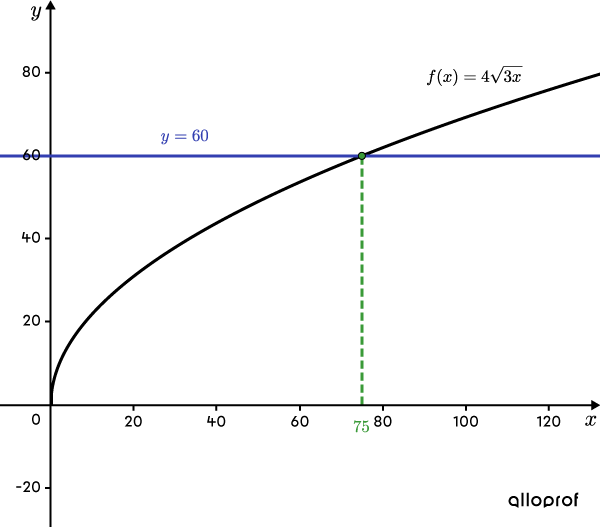
Le graphique ci-contre représente la fonction |f(x)=4\sqrt{3x}| ainsi que la droite |\color{#333fb1}{y=60}.| On remarque que la droite croise la fonction racine carrée en un point. La coordonnée en |x| de ce point correspond à la valeur calculée à l’étape 4.
La solution de l’équation |4\sqrt{3x}=60| est |\color{#3A9A38}{x\color{black}{=}75}.|
Il y a 2 façons de valider la solution à l’étape 5.
-
S’assurer que la solution respecte la restriction déterminée à l’étape 2, comme le montre l’exemple précédent.
-
Substituer la solution dans l’équation de départ. Dans l’exemple précédent, on remplace la variable |x| dans l’équation |4\sqrt{3x}=60| et on s’assure que le membre de gauche est équivalent au membre de droite.
||\begin{align}4\sqrt{3\color{#EC0000}{x}}&=60\\4\sqrt{3(\color{#EC0000}{75})}&\overset{?}{=}60\\4\sqrt{225}&\overset{?}{=}60\\60&=60\end{align}||Cette dernière égalité est vraie, ce qui implique que la solution |x=75| est valide.
Résous l'équation |\sqrt{x-7}+2=9.|
-
Isoler la racine carrée
||\begin{align}\sqrt{x-7}+2&=9\\\sqrt{x-7}&=7\end{align}|| -
Calculer les restrictions
On remarque que |\sqrt{x-7}| est supérieure à |0| puisque c’est égal à |7.| Ceci implique qu’il existe au moins une solution. Pour la deuxième restriction, on a :||\begin{align}x-7&\ge0\\x&\ge7\end{align}|| -
Élever au carré les 2 membres de l’équation
||\begin{align}\sqrt{x-7}&=7\\\color{#EC0000}{(\color{black}{\sqrt{x-7}})^2}&=7^{\color{#EC0000}{2}}\end{align}|| -
Résoudre l’équation obtenue
||\begin{align}x-7&=49\\\color{#3A9A38}{x}&=\color{#3A9A38}{56}\end{align}|| -
Valider la solution obtenue
La restriction |x\ge7| calculée à l’étape 2 est respectée, car |\color{#3A9A38}{56}\ge7.| -
Donner la solution
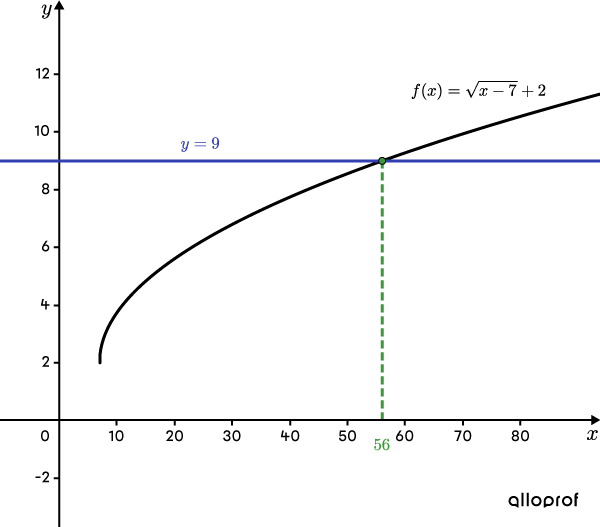
Le graphique ci-contre représente la fonction |f(x)=\sqrt{x-7}+2| ainsi que la droite |\color{#333fb1}{y=9}.| On remarque que la droite croise la fonction racine carrée en un point. La coordonnée en |x| de ce point correspond à la valeur calculée à l’étape 4.
La solution de l’équation |\sqrt{x-7}+2=9| est |\color{#3A9A38}{x\color{black}{=}56}.|
Voici un exemple où l’équation ne possède aucune solution.
Résous l’équation |2\sqrt{x+1}+3=1.|
-
Isoler la racine carrée
||\begin{align}2\sqrt{x+1}+3&=1\\2\sqrt{x+1}&=-2\\\sqrt{x+1}&=-1\end{align}|| -
Calculer les restrictions
Une racine carrée doit toujours être supérieure ou égale à |0,| ce qui n’est pas le cas ici, puisqu’on obtient l’équation |\sqrt{x+1}=-1.|
Ce graphique représente la fonction |f(x)=2\sqrt{x+1}+3| ainsi que la droite |\color{#333fb1}{y=1}.| On remarque que la droite ne rencontre jamais la fonction racine carrée. Puisqu’il n’y a aucun point d’intersection, il n’y a aucune solution à l’équation |2\sqrt{x+1}+3=1.|

Voici un exemple où la résolution fait apparaitre une équation de degré 2.
Résous l'équation |3\sqrt{x+3}-6=x-2.|
-
Isoler la racine carrée
||\begin{align}3\sqrt{x+3}-6&=x-2\\3\sqrt{x+3}&=x+4\\\sqrt{x+3}&=\dfrac{x+4}{3}\end{align}|| -
Calculer les restrictions
On remarque que |\sqrt{x+3}| est supérieure ou égale à |0| si et seulement si |\dfrac{x+4}{3}| l’est aussi. Il est donc nécessaire d’analyser cette restriction.||\begin{align}\dfrac{x+4}{3}&\ge0\\x+4&\ge0\\x&\ge-4\end{align}||Ceci implique qu’il existe au moins une solution si et seulement si |x\ge-4.| On trouve la restriction pour que le terme sous la racine soit positif.||\begin{align}x+3&\ge0\\x&\ge-3\end{align}||On se retrouve avec |2| restrictions où |x\ge-4| et |x\ge-3.| Il arrive parfois, comme c’est le cas ici, qu’une des |2| restrictions qu’on obtient soit inutile. En effet, on remarque qu’il est suffisant d’utiliser uniquement la restriction |x\ge-3,| puisqu’un nombre |x| qui est plus grand que |-3| est nécessairement plus grand que |-4.| On ne retient alors que |x\ge-3.| -
Élever au carré les 2 membres de l’équation
||\begin{align}\sqrt{x+3}&=\dfrac{x+4}{3}\\\color{#EC0000}{(\color{black}{\sqrt{x+3}})^2}&=\color{#EC0000}{\left(\color{black}{\dfrac{x+4}{3}}\right)^2}\end{align}|| -
Résoudre l’équation obtenue
Puisqu’il s’agit d’une équation de degré 2, il est préférable de la transformer pour qu’elle soit égale à |0.|||\begin{align}x+3&=\dfrac{x^2+8x+16}{9}\\9(x+3)&=x^2+8x+16\\9x+27&=x^2+8x+16\\0&=x^2-x-11\end{align}||On peut maintenant utiliser la formule quadratique pour trouver les valeurs de |x.|||\begin{align}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\&=\dfrac{-(-1)\pm\sqrt{(-1)^2-4(1)(-11)}}{2(1)}\\&=\dfrac{1\pm\sqrt{45}}{2}\\\color{#3A9A38}{x}&\in\{\color{#3A9A38}{-2{,}85};\color{#3A9A38}{3{,}85}\}\end{align}|| -
Vérifier les solutions obtenues
La restriction |x\ge-3| calculée à l’étape 2 est respectée dans les 2 cas, car |\color{#3A9A38}{-2{,}85}\ge-3| et |\color{#3A9A38}{3{,}85}\ge-3.| -
Donner l’ensemble-solution
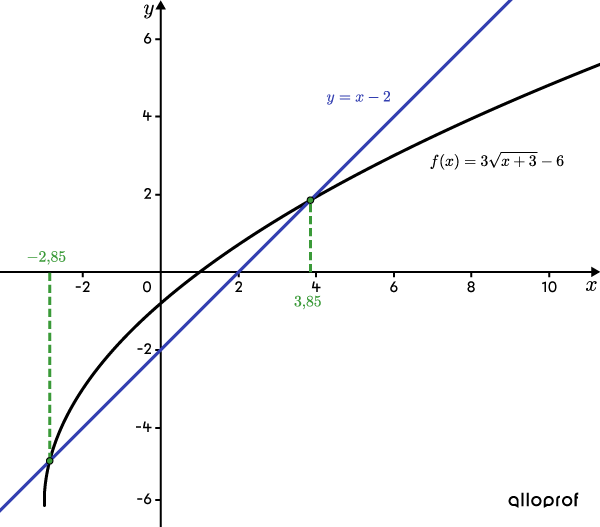
Le graphique ci-contre représente la fonction |f(x)=3\sqrt{x+3}-6| ainsi que la droite |\color{#333fb1}{y=x-2}.| On remarque que la droite croise la fonction racine carrée en 2 points. La coordonnée en |x| pour chacun de ces points correspond à l’une des valeurs calculées à l’étape 4.
L’ensemble-solution de l’équation |3\sqrt{x+3}-6=x-2| est |x\in\{\color{#3A9A38}{-2{,}85};\color{#3A9A38}{3{,}85}\}.|
Voici un autre exemple pour lequel il n’y a aucune solution à l’équation.
Résous l'équation |\sqrt{x-3}+\sqrt{x}=1.|
-
Isoler l’une des racines carrées
||\begin{align}\sqrt{x-3}+\sqrt{x}&=1\\\sqrt{x-3}&=1-\sqrt{x}\end{align}|| -
Calculer les restrictions
On remarque que |\sqrt{x-3}| est supérieure à |0| si et seulement si |1-\sqrt{x}| l’est aussi. Il est donc nécessaire d’analyser cette restriction.||\begin{align}1-\sqrt{x}&\ge0\\1&\ge\sqrt{x}\\1^\color{#EC0000}{2}&\ge\color{#EC0000}{(\color{black}{\sqrt{x}})^2}\\1&\ge x\end{align}||Ceci implique qu’il existe au moins une solution si et seulement si |x\le1.| On trouve la restriction pour que le terme sous la racine soit positif.||\begin{align}x-3&\ge0\\x&\ge3\end{align}||On se retrouve avec |2| restrictions contradictoires où |x\le1| et |x\ge3.| Puisqu’il n’existe aucun nombre qui est à la fois plus petit que |1| et plus grand que |3,| on en conclut qu’il n’existe aucune solution à l’équation |\sqrt{x-3}+\sqrt{x}=1.|
La méthode pour résoudre une inéquation contenant une racine carrée est très similaire à celle employée pour résoudre une équation de racine carrée. La différence la plus importante est qu’il est toujours préférable de tracer une esquisse du graphique de la fonction ou une droite numérique lorsqu’on conclut la résolution. Avec les restrictions et le support visuel, il est alors plus facile d’identifier correctement l’ensemble-solution de l’inéquation.
-
Remplacer le symbole d’inégalité par le symbole d’égalité.
-
Isoler la racine carrée.
-
Vérifier si la racine carrée est supérieure ou égale à |0| et calculer la restriction, au besoin.
-
Élever au carré les 2 membres de l’équation.
-
Résoudre l’équation.
-
Valider l’ensemble-solution de l’équation.
-
Déterminer l’ensemble-solution de l’inéquation à l’aide d’un graphique ou d’une droite numérique.
Résous l'inéquation |\sqrt{x-3}>2.|
-
Remplacer le symbole d’inégalité par le symbole d’égalité
||\sqrt{x-3}=2|| -
Isoler la racine carrée
La racine carrée est déjà isolée. -
Calculer les restrictions
On remarque que |\sqrt{x-3}| est supérieure à |0| puisque c’est égal à |2.| Ceci implique qu’il existe au moins une solution. Quant à la restriction sous la racine, on a :||\begin{align}x-3&\ge0\\x&\ge3\end{align}|| -
Élever au carré les 2 membres de l’équation
||\begin{align}\sqrt{x-3}&=2\\\color{#EC0000}{(\color{black}{\sqrt{x-3}})^2}&=\color{#EC0000}{\left(\color{black}{2}\right)^2}\end{align}|| -
Résoudre l’équation
||\begin{align}x-3&=4\\x&=7\end{align}|| -
Valider la solution de l’équation
La valeur |x=7| est valide puisqu’elle respecte la restriction |x\ge3| calculée à l’étape 3. -
Déterminer l’ensemble-solution de l’inéquation
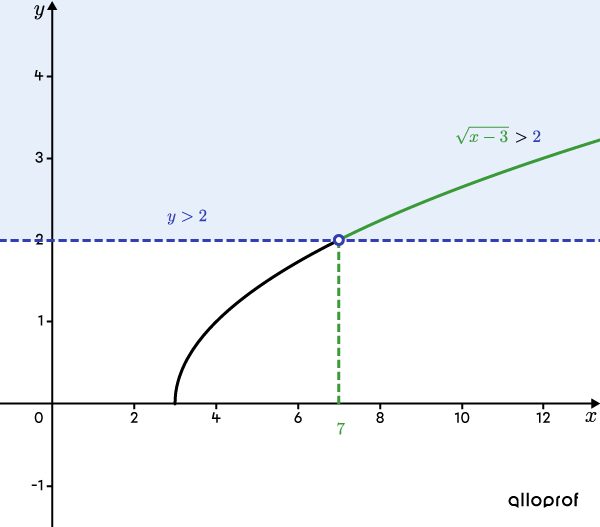
Pour déterminer l’ensemble-solution, on peut tracer le graphique de la fonction racine carrée |f(x)=\sqrt{x-3}.| Voici comment procéder.
Le sommet de la fonction |f(x)=\sqrt{x-3}| est en |(3,0),| car |h=3| et |k=0.| De plus, on sait, grâce à l’étape 5, que cette fonction passe par le point |\color{#333fb1}{(7,2)}.| Avec ces 2 points, on trace la courbe de la racine carrée.
On délimite ensuite le plan cartésien en traçant la droite d’équation |\color{#333fb1}{y=2}| et on indique la région à analyser. Dans ce cas-ci, il est préférable que la droite soit pointillée pour bien représenter qu’on ne s’intéresse qu’aux points de la courbe où |f(x)| est strictement supérieure à 2.
En analysant le graphique, on déduit que l’ensemble-solution est compris entre |7| exclusivement et |+\infty.|
L’ensemble-solution à l'inéquation |\sqrt{x-3}>2| est |x\in\ ]7,+\infty[.|
Tracer le graphique de la fonction pour déterminer l’ensemble-solution à l’étape 7 n’est pas la seule option. En effet, il arrive parfois qu’une droite numérique soit suffisante pour arriver à la même conclusion. Voici comment procéder.
On trace d’abord une droite numérique, puis on représente par un point plein la restriction |x\ge3| déterminée à l’étape 3. On place ensuite un point vide à |x=7,| la solution obtenue à l’étape 5. Le point est vide, car le radical |\sqrt{x-3}| est strictement supérieur à |2.|
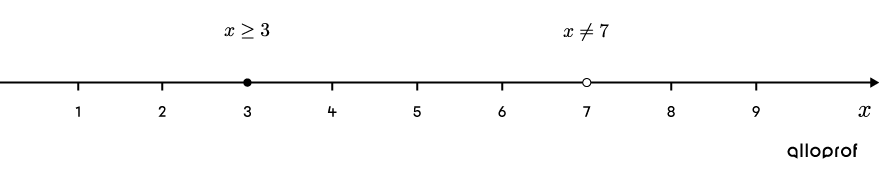
Ces 2 valeurs de |x| séparent la droite numérique en 3 intervalles : |]-\infty, 3],| |[3,7[| et |]7,+\infty[.| Il faut donc valider une valeur au hasard dans chacune de ces sections dans l’inéquation de départ. Il n’est pas nécessaire de vérifier l’intervalle |]-\infty,3[,| car comme il a été démontré à l’étape 3, la solution à l’inéquation doit être supérieure ou égale à |3.|
-
Pour |[3,7[,| on utilise |x=5.|
||\begin{align}\sqrt{\color{#3A9A38}{x}-3}&>2\\\sqrt{\color{#3A9A38}{5}-3}&\stackrel{?}{>}2\\\sqrt{2}&\not>2\end{align}||Ceci est impossible et implique que l’intervalle |[3,7[| ne fait pas partie de l’ensemble-solution.
-
Pour |]7,+\infty[,| on utilise |x=9.|
On obtient |\sqrt{6}>2,| qui est vrai. L’intervalle |]7,+\infty[| fait donc partie de l’ensemble-solution.
Sur la droite numérique, on peut finalement colorier la section qui correspond à l’ensemble-solution.
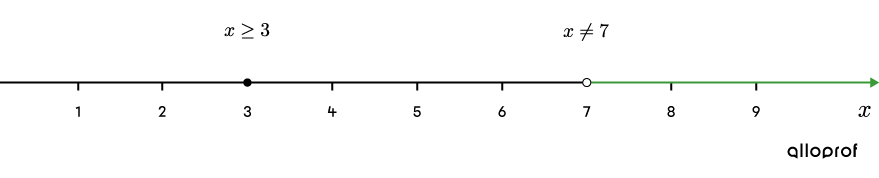
Ainsi, comme avec la méthode graphique, on en conclut que l'ensemble-solution à l’inéquation |\sqrt{x-3}>2| est |]7,+\infty[.|
Voici un exemple où la résolution se fait à l’aide d’une droite numérique.
Résous l'inéquation |\sqrt{2x-5}\le5.|
-
Remplacer le symbole d’inégalité par le symbole d’égalité
||\sqrt{2x-5}=5|| -
Isoler la racine carrée
La racine carrée est déjà isolée. -
Calculer les restrictions
On remarque que |\sqrt{2x-5}| est supérieure à |0| puisque c’est égal à |5.| Ceci implique qu’il existe au moins une solution. Quant à la restriction sous la racine, on a :||\begin{align}2x-5&\ge0\\2x&\ge5\\x&\ge\dfrac{5}{2}\end{align}||Sur une droite numérique, on indique cette restriction avec un point plein.
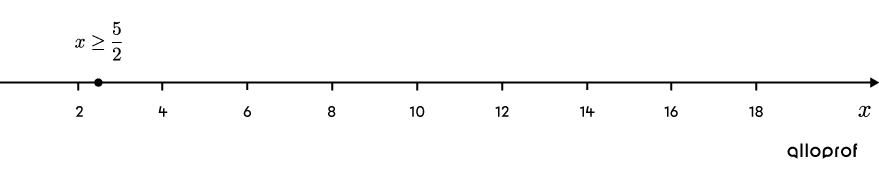
-
Élever au carré les 2 membres de l’équation
||\begin{align}\sqrt{2x-5}&=5\\\color{#EC0000}{(\color{black}{\sqrt{2x-5}})^2}&=\color{#EC0000}{\left(\color{black}{5}\right)^2}\end{align}|| -
Résoudre l’équation
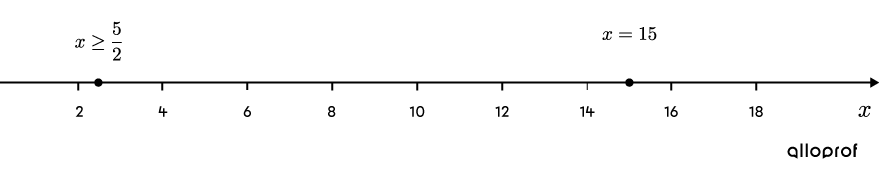
||\begin{align}2x-5&=25\\2x&=30\\x&=15\end{align}||On ajoute un point plein à |x=15| sur la droite numérique. Le point est plein, car le symbole de l’inéquation est |\le.|
-
Valider la solution de l’équation
La valeur |x=15| est valide, puisqu’elle respecte la restriction |x\ge\dfrac{5}{2}| calculée à l’étape 3. -
Déterminer l’ensemble-solution de l’inéquation
On peut maintenant vérifier quel intervalle fait partie de l’ensemble-solution en remplaçant |x| dans l’inéquation d’origine. Il n’est pas nécessaire de vérifier l’intervalle |\left]-\infty,\dfrac{5}{2}\right[,| puisqu’on a démontré à l’étape 3 que la solution de l’inéquation n’est pas dans cet intervalle.
On prend une valeur de |x| entre |\dfrac{5}{2}| et |15,| par exemple |x=10.| On a :||\begin{align}\sqrt{2\color{#EC0000}{x}-5}&\le5\\\sqrt{2(\color{#EC0000}{10})-5}&\stackrel{?}{\le}5\\\sqrt{15}&\stackrel{?}{\le}5\\3{,}87&\le5\end{align}||Cette inégalité est vraie, ce qui implique que l’intervalle |\left[\dfrac{5}{2},15\right]| fait partie de l’ensemble-solution. De la même façon, en remplaçant |x| par un nombre supérieur à |15,| comme |x=20,| on trouve que l’intervalle |]15,+\infty[| ne fait pas partie de l’ensemble-solution.

L’ensemble-solution à l'inéquation |\sqrt{2x-5}\le5| est |\left[\dfrac{5}{2},15\right].|
Voici un exemple dans lequel la fonction racine carrée croise une fonction affine. Lorsque cette situation se présente, on doit résoudre une équation de degré 2 et ne conserver qu’une des 2 solutions.
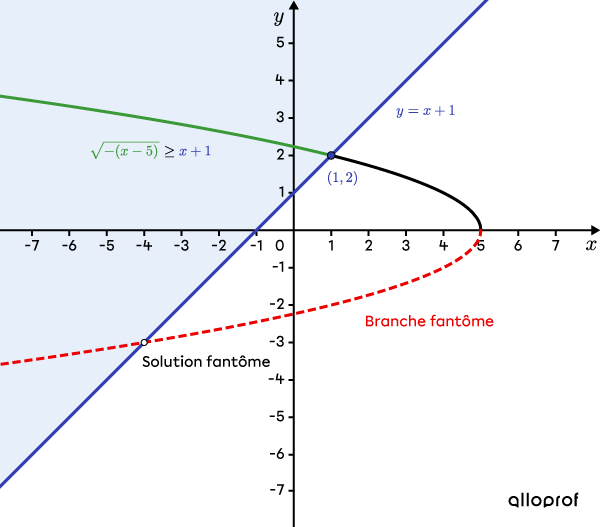
Résous l'inéquation |\sqrt{-(x-5)}\ge x+1.|
-
Remplacer le symbole d’inégalité par le symbole d’égalité
||\sqrt{-(x-5})=x+1|| -
Isoler la racine carrée
La racine carrée est déjà isolée. -
Calculer les restrictions
Dans l’équation, |\sqrt{-(x-5)}| est supérieure ou égale à |0| si et seulement si la restriction suivante est respectée.||\begin{align}x+1&\ge0\\x&\ge-1\end{align}||Pour la restriction sous la racine, on a :||\begin{align}-(x-5)&\ge0\\\color{#EC0000}{-1\times}-(x-5)&\color{#EC0000}{\le}0\color{#EC0000}{\times-1}\\x-5&\le0\\x&\le5\end{align}|| -
Élever au carré les 2 membres de l’équation
||\begin{align}\sqrt{-(x-5)}&=x+1\\\color{#EC0000}{\left(\color{black}{\sqrt{-(x-5)}}\right)^2}&=\color{#EC0000}{\left(\color{black}{x+1}\right)^2}\end{align}|| -
Résoudre l’équation
On peut d’abord transformer l’équation pour qu’elle soit égale à |0,| ce qui permet ensuite d’utiliser la formule quadratique.||\begin{align}-(x-5)&=x^2+2x+1\\-x+5&=x^2+2x+1\\0&=x^2+3x-4\\\\x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\x&=\dfrac{-(3)\pm\sqrt{(3)^2-4(1)(-4)}}{2(1)}\\\\x&=\dfrac{-3\pm\sqrt{25}}{2}\\\\x&\in\{-4,1\}\end{align}|| -
Valider les solutions de l’équation
La valeur |x=-4| n’est pas valide, puisqu’elle ne respecte pas la restriction |x\ge-1| calculée à l’étape 3. Par contre, la valeur |x=1| est valide, car elle respecte à la fois les restrictions |x\ge-1| et |x\le5.| -
Déterminer l’ensemble-solution de l’inéquation
Pour déterminer l’ensemble-solution, on peut tracer le graphique de la fonction racine carrée |f(x)=\sqrt{-(x-5)}.| Voici comment procéder.
La fonction |f(x)=\sqrt{-(x-5)}| a son sommet en |(5,0)| et passe par le point |\color{#333fb1}{(1,2)}.| Avec ces 2 points, on trace la courbe de la racine carrée.
On délimite ensuite le plan cartésien en traçant la droite d’équation |\color{#333fb1}{y=x+1}| et on indique la région à analyser. Dans ce cas-ci, il est préférable que la droite soit pleine pour bien représenter qu’on s’intéresse aux points de la courbe où |f(x)| est supérieure ou égale à |\color{#333fb1}{x+1}|.
En analysant le graphique, on déduit que l’ensemble-solution à l'inéquation |\sqrt{-(x-5)}\ge x+1| est |]-\infty,1].|
Remarque : La branche fantôme est une conséquence des manipulations algébriques effectuées à l’étape 4. En effet, en élevant au carré les 2 membres de l’équation, on génère cette deuxième branche. Cette branche croise la droite |\color{#333fb1}{y=x+1}| en |x=-4| et c’est la raison pour laquelle on doit rejeter cette solution à l’étape 6.