L'équation de la fonction racine carrée peut s'écrire |f(x)=a\sqrt{bx}| où |a| et |b| sont tous deux non nuls.
Remarque : Lorsque |a=1| et |b=1|, on obtient l'équation |f(x)=\sqrt{x}| qui correspond à la forme de base de la fonction racine carrée.
Cette fiche traite de la fonction racine carrée présentée ci-haut ainsi que du comportement de quelques-uns de ses paramètres. Pour des informations supplémentaires, vous pouvez consulter les fiches suivantes.
Si on note |x| l'aire d'un carré et |y| la mesure du côté, on obtient alors l'équation |f(x)=\sqrt{x}|. Ici, |a=1| et |b=1|. Le graphique ci-dessous nous permet de voir l'allure de cette fonction racine carrée.
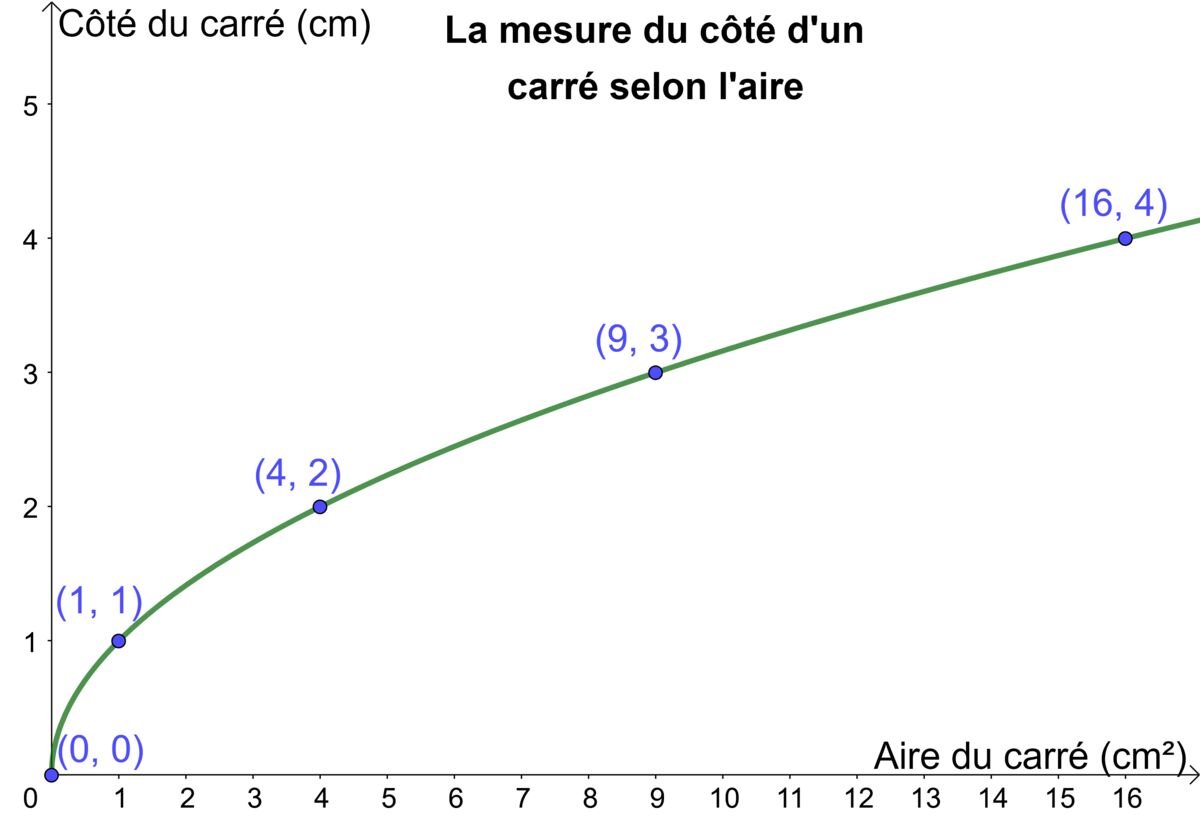
| |x| | |y| |
|---|---|
| |1| | |1| |
| |4| | |2| |
| |9| | |3| |
| |16| | |4| |
On remarque qu'il y a un sommet et qu'il se situe toujours à l'origine |(0,0)| lorsque l'équation est de la forme |f(x)=a\sqrt{bx}.|
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction racine carrée de façon interactive, consulte la MiniRécup suivante.
