En ce qui concerne la rotation, il s'agit d'une autre transformation géométrique que l'on peut qualifier d'isométrique.
La rotation, notée |r_{(\text{centre}, \text{degré})}|, est une transformation géométrique qui permet d'obtenir l'image d'une figure initiale suite à un « glissement », défini selon un degré et un sens, autour d'un point appelé centre de rotation.
Dans une rotation r:
- le centre de rotation P est un point fixe autour duquel se fait la rotation;
- l'angle de rotation, généralement représenté par une flèche de rotation, est une mesure en degrés qui indique la valeur de rotation;
- le sens de rotation peut être horaire (dans le sens des aiguilles d'une montre) ou antihoraire (dans le sens contraire des aiguilles d'une montre).
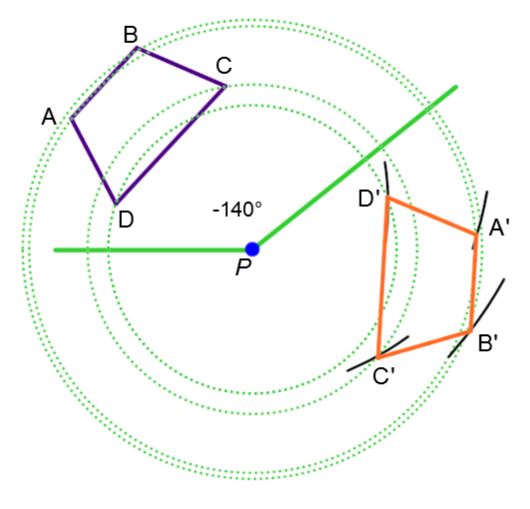
La figure image |A'B'C'| est le résultat d’une rotation de |72^\circ| de la figure initiale |ABC| autour du point |D.|
Fait à noter, il faut porter une attention particulière au signe qui définit l'angle de rotation. En d'autres mots, il faut bien associer un signe positif ou négatif avec une rotation horaire ou anti-horaire.
Lorsque la rotation s’effectue dans le sens des aiguilles d’une horloge, elle est négative. Quand elle s’effectue dans le sens contraire, elle est positive.
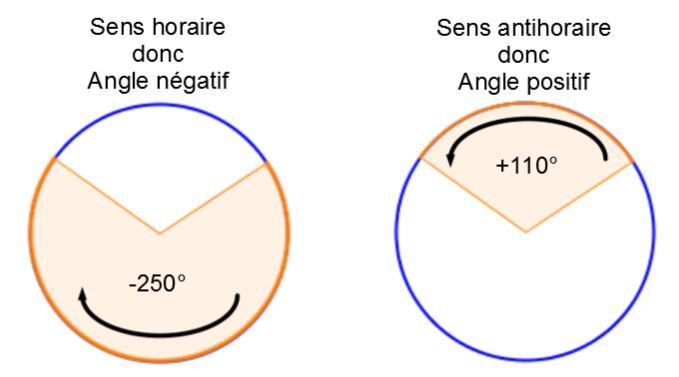
Le sens positif et négatif est en lien avec la numérotation des quadrants dans le plan cartésien.
Ainsi, tous les points de l'image issue d'une rotation peuvent être associés aux points correspondants de la figure initiale. Mathématiquement parlant, on qualifie d'homologues les points qui occupent la même position dans les figures initiale et image.
Afin de distinguer les points homologues de la figure initiale et de la figure image, on utilise de symbole « ' » (nommé prime). Ainsi, le sommet A de la figure initiale devient le sommet A' dans la figure image.
Afin de vérifier qu'une image a été obtenue par rotation, ou encore pour démontrer la construction d'une image par rotation, on peut utiliser les propriétés de la rotation.
| Propriétés de la rotation | Exemple |
|---|---|
|
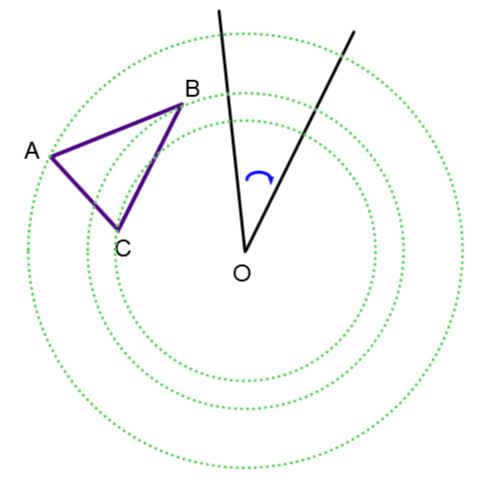
Les côtés homologues d'une figure initiale et de son image ne sont pas nécessairement parallèles. |
|\overline{AB}\not\parallel\overline{A'B'}|, |\overline{BC}\not\parallel\overline{B'C'}|, |\overline{AC}\not\parallel\overline{A'C'}|  |
|
La rotation conserve l'orientation donc l'ordre des sommets homologues est conservé. |
Les sommets |A|, |B| et |C| sont placés dans 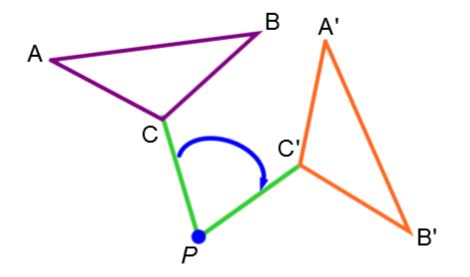
|
|
Les segments de droite tracés pour relier les sommets homologues ne sont jamais parallèles. |
|\overline{AA'}\not\parallel\overline{BB'}\not\parallel\overline{CC'}| 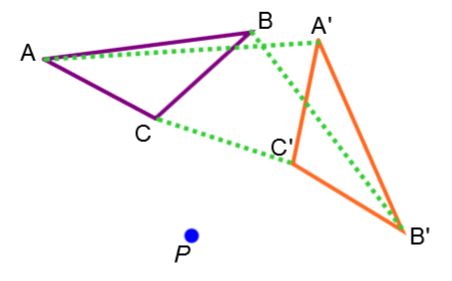 |
On peut effectuer la construction d'une image par rotation de deux façons :
On peut tracer l'image d'une figure par rotation en suivant les étapes suivantes.
-
Placer la pointe sèche du compas sur le centre de rotation P et tracer des cercles passant par chaque sommet de la figure.
-
Pour un sommet de la figure, ouvrir le compas selon l'ouverture équivalant à l'arc de cercle délimité par l'angle de rotation et son cercle respectif.
-
Placer la pointe sèche du compas sur le sommet choisi à l'étape 2 et tracer un petit arc sur son cercle associée en respectant le sens indiqué par la flèche de rotation.
-
Refaire les étapes 2 et 3 pour les autres sommets de la figure.
-
Identifier les points images obtenus par le symbole « ' » pour ensuite utiliser une règle afin de relier les points images de la même façon que les points initiaux.
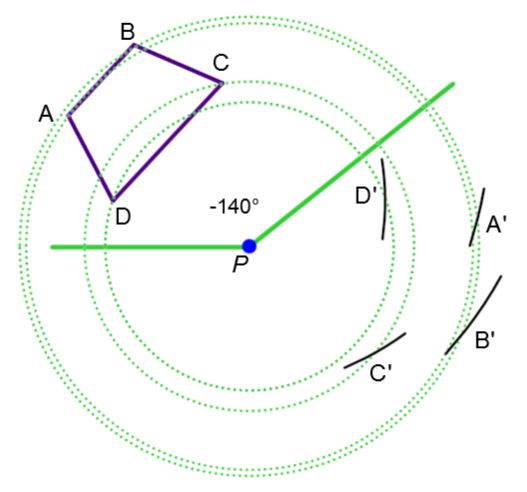
Supposons que l'on veut tracer la figure image du polygone ci-dessous par rotation, on peut suivre les étapes suivantes.
|
1.Placer la pointe sèche du compas sur le centre de rotation P et tracer des cercles passant par chaque sommet de la figure. |
2.Pour un sommet de la figure, ouvrir le compas selon l'ouverture équivalant à l'arc de cercle délimité par l'angle de rotation et son cercle respectif . |
|
3. Placer la pointe sèche du compas sur le sommet choisi à l'étape 2 et tracer un petit arc sur son cercle associée en respectant le sens indiqué par la flèche de rotation. |
4.Refaire les étapes 2 et 3 pour les autres sommets de la figure. |
|
5.Identifier les points images obtenus par le symbole «'» pour ensuite utiliser une règle afin de relier les points images de la même façon que les points initiaux. |
|
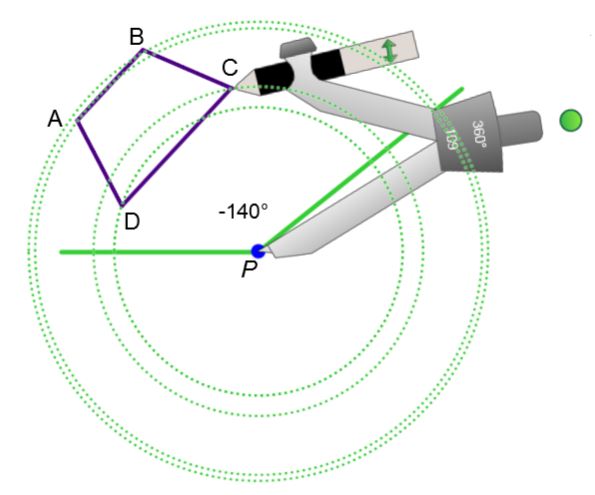
On peut tracer l'image d'une figure par rotation en suivant les étapes suivantes.
-
Pour chacun des sommets, construire des cercles de centre O sur lesquels on effectue la rotation.
-
À l'aide du rapporteur d'angle, mesurer l'angle de rotation et le reporter en plaçant l'origine du rapporteur sur le centre de rotation O et le zéro aligné avec le sommet concerné.
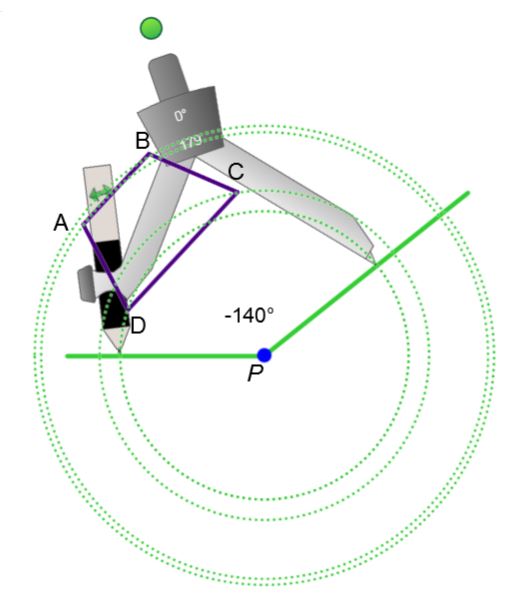
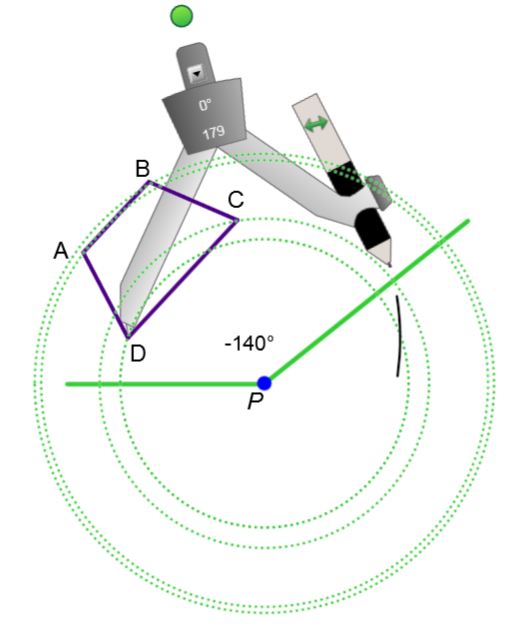
-
Recommencer l'étape 2 pour les autres sommets de la figure pour former les sommets images.
-
Identifier et relier les sommets images pour former la figure image.
Supposons que l'on veut tracer la figure image du polygone ci-dessous par rotation, on peut suivre les étapes suivantes.
|
1. Pour chacun des sommets, construire des cercles de centre O sur lesquels on effectue la rotation. |
2. À l'aide du rapporteur d'angle, mesurer l'angle de rotation et le reporter en placant l'origine du rapporteur sur le centre de rotation O et le zéro aligné avec le sommet concerné. |
|
3. Recommencer l'étape 2 pour les autres sommets de la figure pour former les sommets images. |
4. Identifier et relier les sommets images pour former la figure image. |
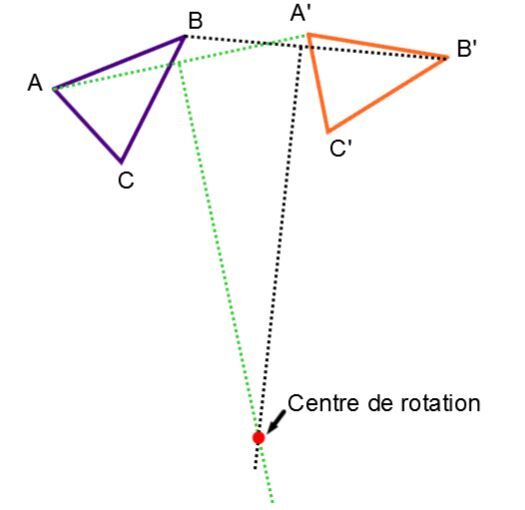
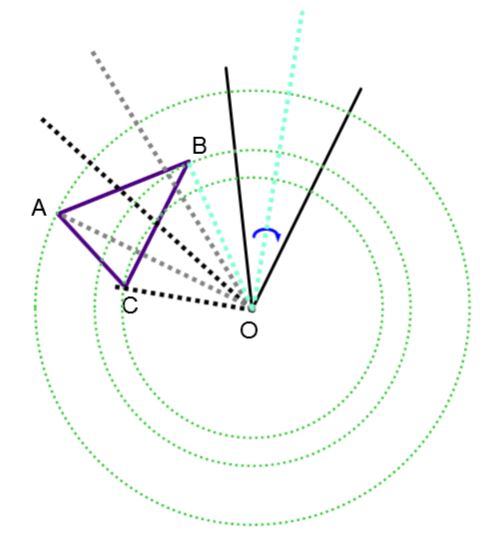
Dans un problème où il faut retrouver le centre de rotation à partir des figures image et initiale, on peut procéder de la façon suivante.
-
Relier entre eux les points homologues (A' avec A, B' avec B,...).
-
Tracer les médiatrices des segments formés.
-
Identifier le point d'intersection des médiatrices comme étant le centre de rotation.
Concrètement, on obtiendrait une démarche semblable à celle qui suit.
Le centre de rotation ci-dessous est situé à la rencontre des médiatrices des segments |\overline{AA'}| et |\overline{BB'}|.