Tout comme chacun des polyèdres réguliers convexes (solides de Platon) le cube possède des caractéristiques très particulières.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p id="definition">Le <strong>cube </strong>est un polyèdre (aussi appelé <a href="/fr/eleves/bv/mathematiques/les-prismes-m1231">prisme</a> ou hexaèdre régulier) qui possède six faces carrées isométriques.<br>
</p>
</body></html>
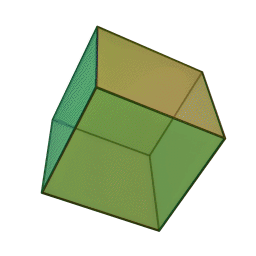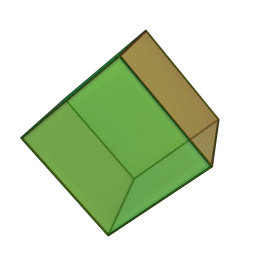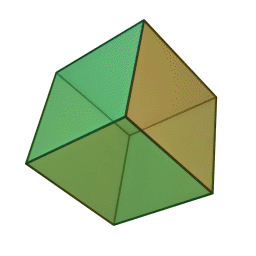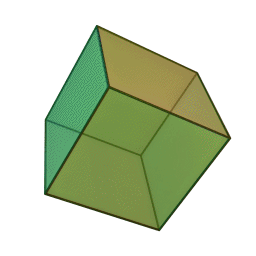
De par sa construction, il est possible d'en déduire d'autres caractéristiques
Pour s'assurer de respecter sa définition et sa construction, il est important de garder ses caractéristiques en tête:
Les caractéristiques du cube sont les suivantes:
- Deux arêtes ayant une extrémité commune sont perpendiculaires
- Les faces opposés sont parallèles
- Les faces adjacentes sont perpendiculaires
- Les diagonales des sommets les plus éloignés se coupent en leur milieu
En respectant chacune de ces propriétés, on obtient toujours le même genre de résultat.
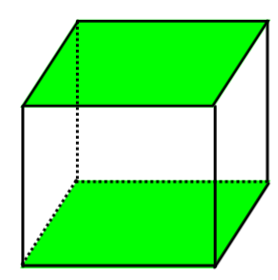
En analysant davantage la composition du cube, on peut trouver d’autres propriétés.
Barycentre
Quand on trace une diagonale entre chaque paire de sommets opposés, on obtient un point d'intersection nommé «barycentre».
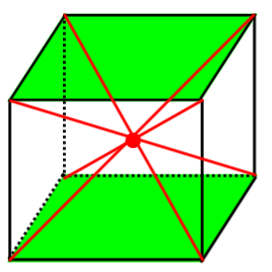
En d'autres mots, il s'agit du centre de gravité du cube. Par ailleurs, si le poids est distribué également dans le cube, il sera alors question d'isobarycentre.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><img alt="La Foire" data-entity-type="file" data-entity-uuid="59ad74a2-8e82-4cca-b48e-6d1abba545ca" src="/sites/default/files/inline-images/LaFoire_4.jpg"></p>
<p><a href="/fr/eleves/bv/jeux/la-foire">Accéder au jeu</a></p>
</body></html>