||V_\text{cube} = c^3|| où ||\begin{align}V&:\text{volume}\\c &: \text{côté}\end{align}||
Remarque : La mesure du côté d’un cube correspond à la longueur de n’importe quelle arête.
À l’aide de la formule précédente, on peut calculer l'espace occupé par un cube, et ce, peu importe la situation.
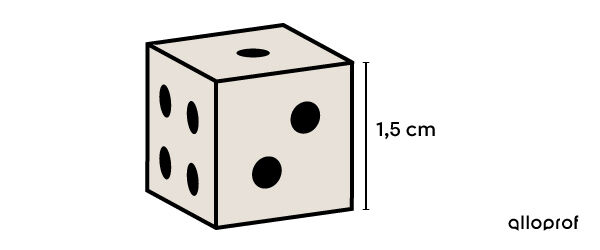
Pour le transport des dés vers la compagnie de polissage, le casino veut empaqueter ses 200 dés dans 5 boites identiques. Quel sera le volume d'une de ces boites?
-
Identifier la nature du solide
Dans le cas présent, il s'agit d'un cube. Ainsi, on utilise la formule du volume : |V = c^3.| -
Appliquer la formule
||\begin{align} V &= c^3\\ &= 1{,}5^3\\ &= 3{,}375 \ \text{cm}^3\end{align}|| -
Interpréter la réponse
Puisqu'il y a |200| dés à déplacer : ||\dfrac {3{,}375\ \text{cm}^3}{1\ \text{dé}} \times 200\ \text{dés} = 675\ \text{cm}^3||
Finalement, on veut empaqueter ces |675 \ \text{cm}^3| dans |5| boites identiques : ||675\ \text{cm}^3 \div 5\ \text{boites} = 135\ \text{cm}^3 / \text{boite}||
Ainsi, chaque boite devra avoir un volume de |135\ \text{cm}^3.|
Dans d'autres circonstances, on pourrait s'intéresser à la mesure du côté alors que le volume est donné. C’est ce qui s’appelle trouver une mesure manquante d'un cube à partir du volume. Dans ce cas, la démarche est un peu différente, mais il demeure essentiel de se rappeler la formule du volume associée au cube.