Pour calculer le périmètre et l’aire des quadrilatères, il faut connaitre la mesure de différents segments comme la base, la hauteur et les diagonales.
Peu importe le quadrilatère, on peut toujours déterminer son périmètre en additionnant la mesure de chacun de ses côtés. Ainsi, on obtient une longueur.
Pour déterminer l’aire d’un quadrilatère, il est possible d’utiliser une feuille quadrillée dont chacun des carrés a une aire précise. En modifiant un peu la figure initiale, on peut arriver à déterminer l'aire du quadrilatère.
En déplaçant certaines parties du quadrilatère original, on peut déduire que ce polygone a une aire de |5\ \text{unités}^2.|
Il est possible de dégager des formules de périmètre et d'aire qui sont spécifiques à chaque quadrilatère en fonction de leurs propriétés. Par ailleurs, ces formules sont très utiles pour trouver des mesures manquantes.
Comme le carré est composé de 4 côtés isométriques et de 4 angles droits, on peut déduire les formules de périmètre et d'aire qui lui sont associées.
||\begin{align}P_\text{carré}&=\color{#3b87cd}a+\color{#ec0000}b+\color{#3a9a38}c+\color{#fa7921}d\\
&=\color{#3a9a38}c+\color{#3a9a38}c+\color{#3a9a38}c+\color{#3a9a38}c\\
&=4\color{#3a9a38}c\end{align}||
Comme on peut le voir, la mesure du côté du carré est la seule information nécessaire pour calculer son périmètre.
Pour marquer un point au baseball, le joueur au bâton doit se rendre à chaque but avant de finalement retourner au marbre. S'il frappe un coup de circuit, le joueur peut parcourir cette distance en toute sécurité.
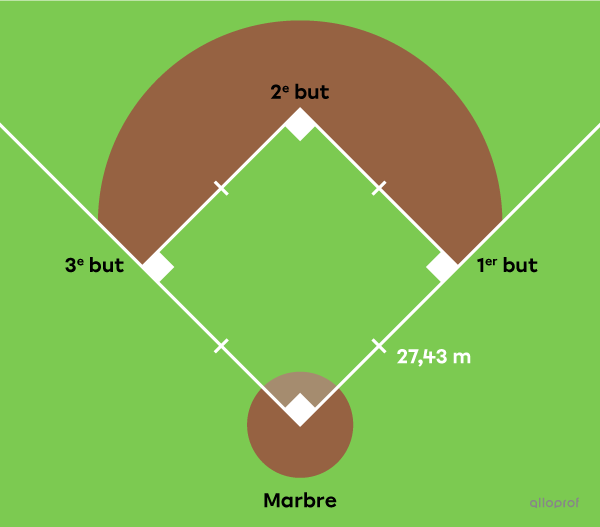
Quelle distance doit parcourir un frappeur qui fait un coup de circuit avant d'atteindre le marbre?
-
Identifier les mesures importantes
||\color{#3a9a38}c=\color{#3a9a38}{27{,}43\ \text{m}}|| -
Déterminer le périmètre
||\begin{align}P_\text{carré}&=4\color{#3a9a38}c\\&=4\times\color{#3a9a38}{27{,}43}\\&=109{,}72\ \text{m}\end{align}|| -
Répondre à la question
Le frappeur doit parcourir une distance de |109{,}72\ \text{m}| avant d'atteindre le marbre.
Tout comme pour le calcul du périmètre, la seule information nécessaire pour calculer l'aire d'un carré est la mesure d'un de ses côtés.
||\begin{align}A_\text{carré}&=\color{#3a9a38}c\times \color{#3a9a38}c\\
&=\color{#3a9a38}c^2\end{align}||
où
|\color{#3a9a38}c :| côté
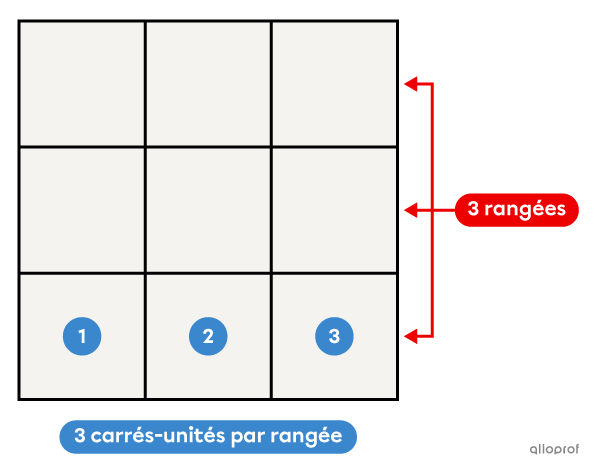
Quand on veut calculer l'aire d'une figure, on cherche à déterminer le nombre de carrés-unités qui la composent.
Il y a |\color{#ec0000}3| rangées de |\color{#3b87cd}3| carrés-unités.||\begin{align}A_\text{carré}&=\text{Nombre total de carrés-unités}\\&=\color{#ec0000}{3}\times\color{#3b87cd}{3}\\&=\color{#ec0000}c\times\color{#3b87cd}c\\&=c^2 \end{align}||
Le propriétaire d'une maison veut connaitre la superficie de son plancher, car il veut y installer du bois franc.
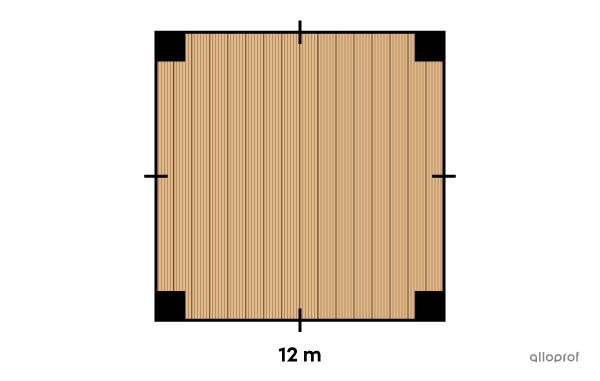
Est-ce qu'il a assez d'un budget de |1\ 000\ $| si le matériau qu'il veut utiliser se vend |9{,}95\ $/\text{m}^2|?
-
Identifier les mesures importantes
||\color{#3a9a38}c=\color{#3a9a38}{12\ \text{m}}|| -
Déterminer l’aire
||\begin{align}A_\text{carré}&=\color{#3a9a38}c^2\\&=\color{#3a9a38}{12}^2\\&=144\ \text{m}^2\end{align}|| -
Répondre à la question
||\text{Cout} =144\times9{,}95=1\ 432{,}80\ \$||
Son budget de |1\ 000\ \$| ne sera pas suffisant pour installer du bois franc sur son plancher.
Dans un rectangle, les côtés opposés sont isométriques et parallèles. C’est une propriété qui est utile pour déterminer ses formules d’aire et de périmètre.
||\begin{align}P_\text{rectangle}&=\color{#ec0000}a+\color{#3b87cd}b+\color{#3a9a38}c+\color{#fa7921}d\\&= \color{#ec0000}h+\color{#ec0000}h+\color{#3b87cd}b+\color{#3b87cd}b\\&=2\color{#ec0000}h+2\color{#3b87cd}b\\&=2 (\color{#ec0000}h+\color{#3b87cd}b)\end{align}||
Comme on peut le voir dans l’encadré précédent, la formule du périmètre du rectangle peut s'écrire de plusieurs façons. Peu importe la formule choisie, le résultat est le même.
Pour bien délimiter son jardin de forme rectangulaire, Julien décide d'installer des bordures de ciment.
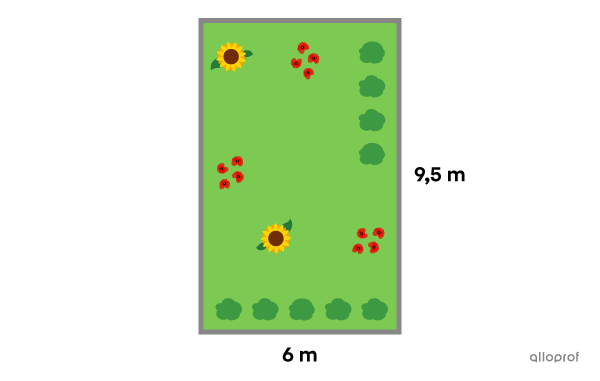
À combien s'élève la facture de cet aménagement si Julien sait qu'un bloc d'une longueur de |90\ \text{cm}| se vend au prix de |8{,}95\ \$|?
-
Identifier les mesures importantes
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{6\ \text{m}}\\\color{#ec0000}h&=\color{#ec0000}{9{,}5\ \text{m}}\end{align}|| -
Déterminer le périmètre
||\begin{align}P_\text{rectangle}&=2(\color{#3b87cd}b+\color{#ec0000}h)\\&=2(\color{#3b87cd}6+\color{#ec0000}{9{,}5})\\&=31\ \text{m}\\&=3\ 100\ \text{cm}\end{align}|| -
Répondre à la question
||\text{Nombre de blocs}=3\ 100 \div 90 \approx 34{,}44||
Comme on cherche un nombre de blocs, la réponse doit être entière. Pour délimiter le jardin, |34| blocs ne sont pas suffisants. Julien doit donc acheter |35| blocs.
||\text{Cout}=35\times8{,}95=313{,}25\ \$||
Julien doit débourser |313{,}25\ \$| pour l’aménagement de son jardin.
Remarque : Les mesures de la base et de la hauteur ont été attribuées au hasard. En effet, le seul lien qu'il y a entre une base et une hauteur est le fait qu’ils sont perpendiculaires. On aurait pu décider que |\color{#3b87cd}{b=9{,}5\ \text{m}}| et que |\color{#ec0000}{h=6\ \text{m}}.| Le résultat aurait été le même.
||A_\text{rectangle}=\color{#3b87cd}b\times\color{#ec0000}h||
où
|\color{#3b87cd}b :| base
|\color{#ec0000}h :| hauteur
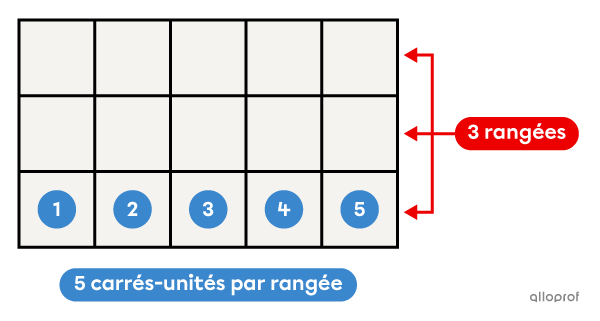
Quand on veut calculer l'aire d'une figure, on cherche à déterminer le nombre de carrés-unités qui la composent. Il suffit de faire une multiplication.
Il y a |\color{#ec0000}3| rangées de |\color{#3b87cd}5| carrés-unités. ||\begin{align}A_\text{rectangle}&=\text{Nombre total de carrés-unités}\\&=\color{#ec0000}3\times\color{#3b87cd}5\\&=\color{#ec0000}h\times\color{#3b87cd}b\end{align}||
Comme la multiplication possède la propriété de la commutativité, on peut affirmer ceci.||A_\text{rectangle}=h\times b=b\times h||
Remarque : Tout comme dans l'application de la formule du périmètre, les mesures de la base et de la hauteur sont attribuées de façon aléatoire, en autant que les 2 segments considérés soient perpendiculaires.
Afin de changer la décoration d’une chambre, on décide de peindre l'un des murs rectangulaires en bleu ciel.

Combien coutera ce changement si on sait qu’un pot de peinture se vend |39{,}95\ \$,| qu'il couvre une superficie de |20\ \text{m}^2| et qu’on doit appliquer 3 couches?
-
Identifier les mesures importantes
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{5{,}2\ \text{m}}\\ \color{#ec0000}h&=\color{#ec0000}{2{,}3\ \text{m}}\end{align}|| -
Déterminer l’aire
||\begin{align}A_\text{rectangle}&= \color{#3b87cd}b\times \color{#ec0000}h\\&=\color{#3b87cd}{5{,}2}\times\color{#ec0000}{2{,}3}\\&=11{,}96\ \text{m}^2\end{align}|| -
Répondre à la question
Puisqu’on doit appliquer 3 couches, la superficie est triplée.||\text{Superficie à peindre}=11{,}96\times3=35{,}88\ \text{m}^2|| ||\text{Nombre de pots nécessaires}=35{,}88\ \text{m}^2\div 20\ \text{m}^2/\text{pot} \approx 1{,}8\ \text{pot}||Comme on doit acheter le pot en entier, il en faut 2.||\text{Cout}=2 \times39{,}95=79{,}90\ \$||La peinture coutera donc |79{,}90\ \$.|
Remarque : Pour les problèmes liés à l'aire d'une figure, il arrive souvent qu'il y ait plus à faire que le simple calcul en lien avec l'application de la formule. Dans ce cas, il est important de bien prendre connaissance du contexte du problème.
Les formules du périmètre et de l'aire du parallélogramme ressemblent beaucoup à celles du rectangle.
||\begin{align}P_\text{parallélogramme}&=\color{#3a9a38}a+\color{#3b87cd}b+\color{#ff55c3}c+\color{#fa7921}d\\&=\color{#3a9a38}a+\color{#3b87cd}b+\color{#3a9a38}a+\color{#3b87cd}b\\&=2\color{#3a9a38}a+2\color{#3b87cd}b\\&=2(\color{#3a9a38}a+\color{#3b87cd}b)\end{align}||
Comme on peut le voir dans l’encadré précédent, la formule du périmètre du parallélogramme peut s'écrire de plusieurs façons. Peu importe la formule choisie, le résultat obtenu est le même.
Amélie court dans un parc sur des sentiers qui, vus de haut, forment un parallélogramme. Elle court à une allure moyenne de |6\ \text{min/km}.| Sachant qu’elle commence devant le grand arbre et termine au même endroit, combien de temps dure sa course?

-
Identifier les mesures importantes
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{1{,}7\ \text{km}}\\\color{#3a9a38}a&=\color{#3a9a38}{1{,}2\ \text{km}}\end{align}|| -
Déterminer le périmètre
||\begin{align}P_\text{parallélogramme}&=2(\color{#3a9a38}a+\color{#3b87cd}b)\\&=2(\color{#3a9a38}{1{,}2}+\color{#3b87cd}{1{,}7})\\&=5{,}8\ \text{km}\end{align}|| -
Répondre à la question
||\text{Temps de course : }5{,}8\ \text{km} \times 6\ \text{min/km} = 34{,}8\ \text{min}||
Amélie court pendant presque |35| minutes.
||A_\text{parallélogramme}=\color{#3b87cd}b\times \color{#ec0000}h||
où
|\color{#3b87cd}b :| base
|\color{#ec0000}h :| hauteur
La formule d'aire du parallélogramme est la même que celle du rectangle. Pour le démontrer, il suffit de prendre une partie du parallélogramme et de la déplacer afin de former un rectangle.
Remarque : La mesure des 2 autres côtés isométriques |(\color{#3a9a38}a)| n'est pas utilisée dans la formule de l’aire.
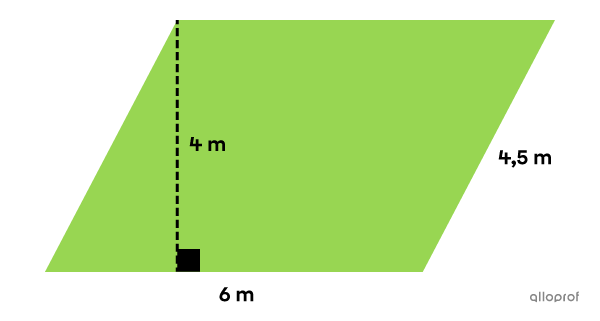
Quelle est l'aire du parallélogramme suivant?
-
Identifier les mesures importantes
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{6\ \text{cm}}\\ \color{#ec0000}h&=\color{#ec0000}{4\ \text{cm}}\end{align}|| -
Déterminer l’aire
||\begin{align}A_\text{parallélogramme}&=\color{#3b87cd}b \times \color{#ec0000}h\\&=\color{#3b87cd}6\times \color{#ec0000}4\\&=24\ \text{cm}^2\end{align}|| -
Répondre à la question
L'aire de ce parallélogramme est de |24\ \text{cm}^2.|
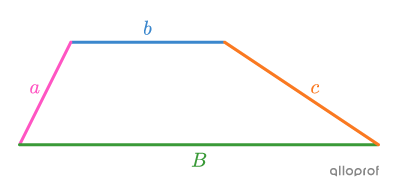
Trapèze
||P_\text{trapèze}= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c||
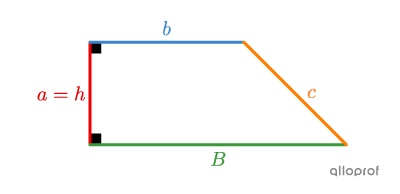
Trapèze rectangle
||\begin{align}P_\text{trapèze rectangle}&= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\\&= \color{#ec0000}h+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\end{align}||

Trapèze isocèle
||\begin{align}P_\text{trapèze isocèle}&= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\\ &= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#ff55c3}a\\ &= 2\color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B\end{align}||
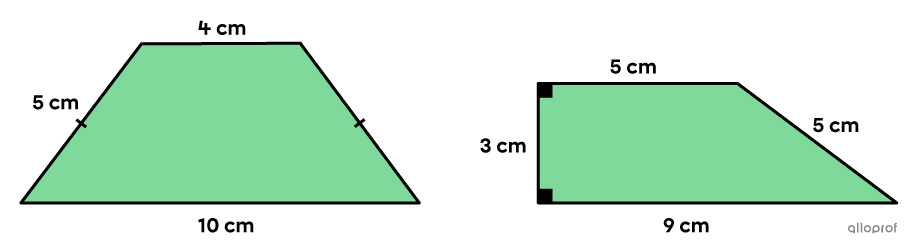
Lequel de ces trapèzes a le plus grand périmètre?
-
Identifier les mesures importantes
Trapèze isocèle
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{4\ \text{cm}}\\\color{#3a9a38}B&=\color{#3a9a38}{10\ \text{cm}}\\\color{#ff55c3}a&=\color{#ff55c3}{5\ \text{cm}}\end{align}||
Trapèze rectangle
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{5\ \text{cm}} \\\color{#3a9a38}B&=\color{#3a9a38}{9\ \text{cm}}\\\color{#ec0000}h&=\color{#ec0000}{3\ \text{cm}}\\\color{#fa7921}c&=\color{#fa7921}{5\ \text{cm}}\end{align}||
-
Déterminer les périmètres
||\begin{align}P_\text{trapèze isocèle}&=2\color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B\\
&=2\times\color{#ff55c3}5+\color{#3b87cd}4+\color{#3a9a38}{10}\\
&=24\ \text{cm}\end{align}||
||\begin{align}P_\text{trapèze rectangle}&=\color{#ec0000}h+ \color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\\
&=\color{#ec0000}3+\color{#3b87cd}5+\color{#3a9a38}9+\color{#fa7921}5\\
&=22 \ \text{cm}\end{align}||
-
Répondre à la question
Le périmètre du trapèze isocèle est le plus grand.
||A_\text{trapèze}=\dfrac{(\color{#3a9a38}{B}+\color{#3b87cd}b)\times\color{#ec0000}h}{2}||
où
|\color{#3a9a38}B :| grande base
|\color{#3b87cd}b :| petite base
|\color{#ec0000}h :| hauteur
Pour bien distinguer chacune des mesures impliquées dans l'utilisation de cette formule, on peut se référer aux propriétés des trapèzes. Il est important de noter que la hauteur représente toujours la distance mesurée perpendiculairement entre les 2 bases.
Pour démontrer cette formule, on utilise des transformations géométriques sur certaines parties d'un trapèze afin de former un rectangle.
De cette façon, on obtient un rectangle dont la mesure de la longueur est de |\color{#3b87cd}b+\color{#3a9a38}B| et dont la hauteur |\color{#ec0000}h| est la même que celle du trapèze. Puisque le rectangle est formé de 2 trapèzes, on doit diviser par 2 pour obtenir l’aire d’un trapèze.
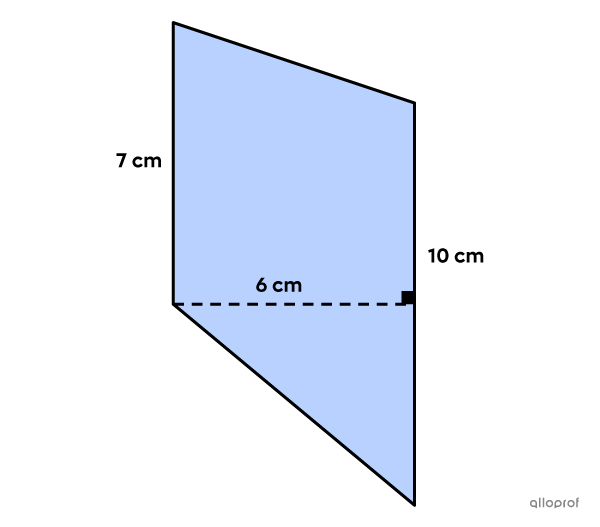
Quelle est l'aire du trapèze suivant?
-
Identifier les mesures importantes
||\begin{align}\color{#3a9a38}B&=\color{#3a9a38}{10\ \text{cm}}\\\color{#3b87cd}b&=\color{#3b87cd}{7\ \text{cm}}\\\color{#ec0000}h&=\color{#ec0000}{6 \ \text{cm}}\end{align}|| -
Déterminer l’aire
||\begin{align}A_\text{trapèze}&=\dfrac{(\color{#3a9a38}B+ \color{#3b87cd}b)\times\color{#ec0000}h}{2}\\&=\dfrac{(\color{#3a9a38}{10}+\color{#3b87cd}7)\times \color{#ec0000}6}{2}\\&=\dfrac{102}{2}\\&=51\ \text{cm}^2\end{align}|| -
Répondre à la question
L'aire de ce trapèze est de |51\ \text{cm}^2.|
Puisqu’il possède 4 côtés isométriques, le losange partage la même formule de périmètre que le carré. Pour déterminer son aire, on doit utiliser ses diagonales.
||\begin{align}P_\text{losange}&=\color{#ff55c3}a+\color{#C58AE1}b+\color{#3a9a38}c+\color{#fa7921}d\\&=\color{#3a9a38}c+\color{#3a9a38}c+\color{#3a9a38}c+\color{#3a9a38}c\\&=4\color{#3a9a38}c\end{align}||
Une seule mesure est nécessaire pour calculer le périmètre d'un losange.
Quel est le périmètre du losange suivant?

-
Identifier les mesures importantes
||\color{#3a9a38}c=\color{#3a9a38}{5{,}12\ \text{dm}}|| -
Déterminer le périmètre
||\begin{align}P_\text{losange}&=4\color{#3a9a38}c\\&=4\times\color{#3a9a38}{5{,}12}\\&=20{,}48\ \text{dm}\end{align}|| -
Répondre à la question
Le périmètre du losange est de |20{,}48\ \text{dm}.|
||A_\text{losange}=\dfrac{\color{#3b87cd}D\times\color{#ec0000}d}{2}||
où
|\color{#ec0000}d :| petite diagonale
|\color{#3b87cd}D :| grande diagonale
La formule de l’aire du losange est en lien avec la formule de l’aire du rectangle. On peut utiliser la rotation pour arriver à créer un rectangle à partir d’un losange.
On obtient un rectangle dont l'aire est donnée par la formule suivante.||\begin{align}A&=\color{#3b87cd}b\times\color{#ec0000}h\\&=\color{#3b87cd}D\times\color{#ec0000}d\end{align}||
Ce rectangle est formé de 2 losanges. Il faut donc diviser l'aire du rectangle par |2| pour obtenir l’aire d’un losange.||A_\text{losange}=\dfrac{\color{#3b87cd}D\times\color{#ec0000}d}{2}||
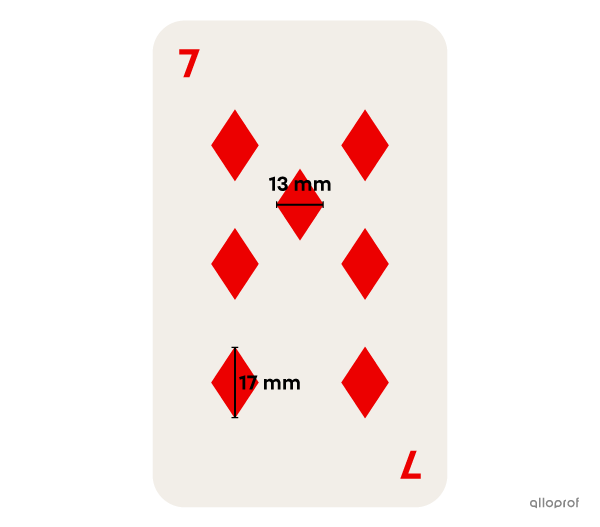
Marc-Antoine a perdu une carte de son jeu de cartes préféré. Il s’agit du 7 de carreau. Puisqu’il a un carton blanc et un peu de peinture rouge, il décide de fabriquer une nouvelle carte, qui remplacera la carte perdue. Les carreaux qu’il fait sont des losanges, tous de la même dimension. Sachant qu’un millilitre couvre environ |180\ \text{mm}^2,| de quelle quantité de peinture aura-t-il besoin?
-
Identifier les mesures importantes
||\begin{align}\color{#3b87cd}D&=\color{#3b87cd}{17\ \text{mm}}\\ \color{#ec0000}d&=\color{#ec0000}{13\ \text{mm}}\end{align}|| -
Déterminer l’aire
||\begin{align}A_\text{losange}&=\dfrac{\color{#3b87cd}D\times \color{#ec0000}d}{2}\\&=\dfrac{\color{#3b87cd}{17}\times\color{#ec0000}{13}}{2}\\&=110{,}5\ \text{mm}^2\end{align}|| -
Répondre à la question
La surface trouvée est pour un carreau. On doit cependant trouver la surface pour les 7 carreaux.||110{,}5 \times 7=773{,}5\ \text{mm}^2||On peut maintenant trouver la quantité de peinture correspondante.||\begin{align}\dfrac{1\ \text{mL}}{180\ \text{mm}^2}&=\ \dfrac{?\ \text{mL}}{773{,}5\ \text{mm}^2}\\\\ ?&=\dfrac{1 \times 773{,}5}{180}\\?&\approx 4{,}3\ \text{mL}\end{align}||Il faudra environ |4{,}3\ \text{mL}| de peinture rouge pour fabriquer la carte perdue.
Pour déterminer le périmètre du cerf-volant, il suffit d'effectuer la somme des mesures des côtés. Pour déterminer l’aire, il faut travailler avec ses diagonales.
||\begin{align}P_\text{cerf-volant}&=\color{#3a9a38}a+\color{#fa7921}b+\color{#ff55c3}c+\color{#C58AE1}d\\&=\color{#3a9a38}a+\color{#3a9a38}a+\color{#fa7921}b+\color{#fa7921}b\\&=2\color{#3a9a38}a+2\color{#fa7921}b\\&=2(\color{#3a9a38}a+\color{#fa7921}b)\end{align}||
Comme on peut le voir dans l’encadré précédent, la formule du périmètre du cerf-volant peut s'écrire de plusieurs façons. Peu importe la formule choisie, le résultat est le même.
Afin de protéger les rebords d’un nouveau cerf-volant, on veut acheter des bordures en plastique.

Quel est le cout total de ce projet si ce type de matériau se vend au prix de |1{,}95\ $| pour |10\ \text{cm}|?
-
Identifier les mesures importantes
||\begin{align}\color{#3a9a38}a&=\color{#3a9a38}{37\ \text{cm}}\\ \color{#fa7921}b&=\color{#fa7921}{52\ \text{cm}} \end{align}|| -
Déterminer le périmètre
||\begin{align}P_\text{cerf-volant}&=2\color{#3a9a38}a+ 2\color{#fa7921}b\\&=2\times\color{#3a9a38}{37}+2\times \color{#fa7921}{52}\\&=178\ \text{cm}\end{align}|| -
Répondre à la question
Puisqu'il en coute |1{,}95\ \$| pour |10\ \text{cm},| on conclut ceci.||\begin{align}\dfrac{1{,}95\ $}{10\ \text{cm}}&=\dfrac{\text{?}}{178\ \text{cm}}\\\\\text{?}&=\dfrac{1{,}95 \times 178}{10}\\\\\text{?}&=34{,}71\ $\end{align}||Pour protéger le cerf-volant, on devra donc débourser |34{,}71\ \$.|
||A_\text{cerf-volant}=\dfrac{\color{#ec0000}D\times \color{#3b87cd}d}{2}||
où
|\color{#ec0000}D :| grande diagonale
|\color{#3b87cd}d :| petite diagonale
La formule de l’aire du cerf-volant est en lien avec la formule de l'aire du rectangle. Pour bien comprendre d'où vient cette formule, on peut se référer à la démonstration de la formule de l'aire du losange.
Avec les conditions météorologiques changeantes, on décide d'appliquer une couche de produit hydrofuge sur la toile d’un cerf-volant afin qu'il ne soit pas abimé par l'eau.

En prenant pour acquis que les 2 côtés du cerf-volant doivent être traités, quelle quantité de produit doit-on acheter si |10\ \text{mL}| peuvent couvrir une surface de |1\ \text{dm}^2|?
-
Identifier les mesures importantes
||\begin{align}\color{#ec0000}D&=\color{#ec0000}{73\ \text{cm}}\\\color{#3b87cd}d&=\color{#3b87cd}{45{,}5\ \text{cm}}\end{align}|| -
Déterminer l’aire
||\begin{align}A_\text{cerf-volant}&=\dfrac{\color{#ec0000}D \times \color{#3b87cd}d}{2}\\&=\dfrac{\color{#ec0000}{73}\times \color{#3b87cd}{45{,}5}}{2}\\&=1\ 660{,}75\ \text{cm}^2\\&\approx 16{,}61\ \text{dm}^2\end{align}|| -
Répondre à la question
Puisqu'il faut |10\ \text{mL}| pour |1\ \text{dm}^2,| on conclut ceci pour un côté du cerf-volant.||\text{Quantité totale}=16{,}61\ \text{dm}^2 \times 10\ \text{mL}/\text{dm}^2 = 166{,}1\ \text{mL}||Comme il faut peindre les 2 faces du cerf-volant, il faut donc |166{,}1 \ \text{mL} \times 2 = 332{,}2\ \text{mL}| de peinture.