Dans les cas où le périmètre d'une figure est connu, il peut arriver qu'on demande de trouver une ou plusieurs mesures manquantes. Pour résoudre les problèmes en lien avec le périmètre, il est utile de connaitre les formules de périmètre des différentes figures planes. Voici les étapes à suivre pour trouver une mesure manquante.
-
Déterminer la formule.
-
Remplacer les variables par les valeurs connues.
-
Isoler la variable recherchée.
-
Répondre à la question.
Voici une série d’exemples. Les premiers sont des problèmes de géométrie qui n’ont pas de contexte particulier, tandis que le dernier est un problème écrit qui présente une courte mise en situation.
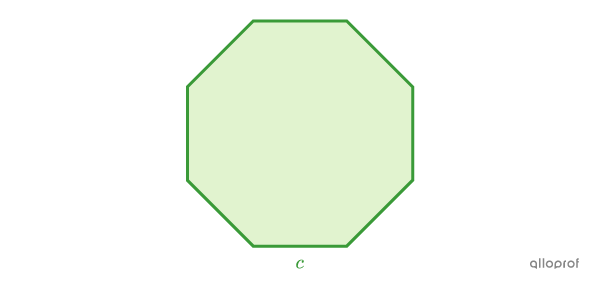
Quelle est la mesure d'un côté d'un octogone régulier dont le périmètre est de |28\ \text{cm}|?
-
Déterminer la formule
On utilise la formule du périmètre d’un polygone régulier.||\begin{align}P&= \text{Somme de tous les côtés}\\ &=8 \times c\end{align}|| -
Remplacer les variables par les valeurs connues
||\begin{align} \color{#3a9a38}{P}&= 8c\\ \color{#3a9a38}{28}&=8c \end{align}|| -
Isoler la variable recherchée
On isole |c| à l’aide de la méthode de la balance.||\begin{align}\color{#ec0000}{\dfrac{\color{black}{28}}{8}}&=\color{#ec0000}{\dfrac{\color{black}{8c}}{8}}\\ 3{,}5 &=c\end{align}|| -
Répondre à la question
La mesure d'un côté de l’octogone régulier est de |3{,}5\ \text{cm}.|
Quelle est la mesure du rayon d'un cercle dont la circonférence est de |110\ \text{cm}|?

-
Déterminer la formule
On utilise la formule de la circonférence d’un cercle.||C= 2 \pi r|| -
Remplacer les variables par les valeurs connues
||\begin{align}\color{#3a9a38}C&=2\pi r\\\color{#3a9a38}{110} &=2\pi r\end{align}|| -
Isoler la variable recherchée
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{110}}{2\pi}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi r}}{2\pi}}\\ 17{,}51&\approx r \end{align}|| -
Répondre à la question
La mesure du rayon est d'environ |17{,}51\ \text{cm}.|
Dans les prochains exemples, il y a plusieurs mesures manquantes. On doit donc utiliser des expressions algébriques pour représenter la mesure des côtés.
Quelles sont les mesures des côtés d'un triangle isocèle qui a un périmètre de |16\ \text{cm}| et dont la mesure des côtés isométriques est de 2 unités supérieures à celle du 3e côté?
-
Déterminer la formule
On utilise la formule du périmètre d’un triangle.
||P= \text{Somme de tous les côtés}|| -
Remplacer les variables par les valeurs connues
Il manque plusieurs informations. On peut faire un dessin pour s’aider à déterminer la mesure des côtés à l’aide de l’algèbre. On associe |x| à la mesure du 3e côté, puisque c’est le côté pour lequel on a le moins d’informations. Ainsi, l’expression algébrique qui représente la mesure des 2 côtés isométriques est |x+2.|
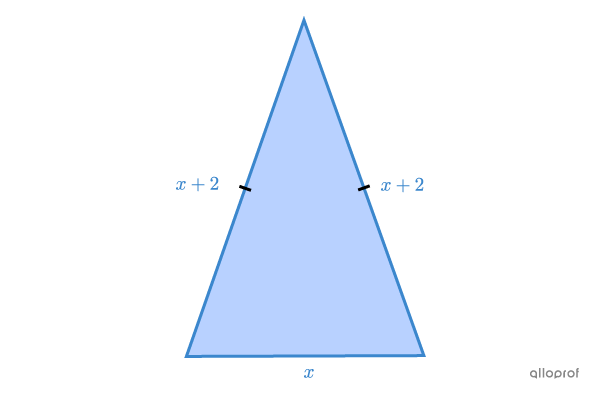
En remplaçant ces informations dans la formule du périmètre, on obtient ceci.
||16=x+(x+2)+(x+2)||
-
Isoler la variable recherchée
On regroupe d’abord les termes semblables, puis on isole |x.|||\begin{align}16&=\color{#3a9a38}x+\color{#3a9a38}x+\color{#3b87cd}2+\color{#3a9a38}x+\color{#3b87cd}2\\16&=\color{#3a9a38}{3x}+\color{#3b87cd}4\\16\color{#ec0000}{-4}&=3x+4\color{#ec0000}{-4}\\12&=3x\\\color{#ec0000}{\dfrac{\color{black}{12}}{3}}&=\color{#ec0000}{\dfrac{\color{black}{3x}}{3}}\\4&=x\end{align}|| -
Répondre à la question
La mesure des côtés isométriques est de |6\ \text{cm},| car |x+2=4 + 2=6,| alors que la mesure du 3e côté est de |4\ \text{cm}.|
Quelles sont les mesures des côtés d'un rectangle qui a un périmètre de |192\ \text{cm}| et dont la mesure de la longueur est le triple de celle de la largeur?
-
Déterminer la formule
On utilise la formule du périmètre d’un rectangle.||P= \text{Somme de tous les côtés}|| -
Remplacer les variables par les valeurs connues
Il manque plusieurs informations. On peut faire un dessin pour s’aider à déterminer la mesure des côtés à l’aide de l’algèbre. On associe |x| à la mesure de la largeur, puisqu’on a moins d’informations sur ce côté. Ainsi, l’expression algébrique qui représente la longueur est |3x.|

En remplaçant ces informations dans la formule du périmètre, on obtient ceci.||192=x+x+(3x)+(3x)||
-
Isoler la variable recherchée
||\begin{align}192&=x+x+3x+3x\\192&=8x\\\color{#ec0000}{\dfrac{\color{black}{192}}{8}}&=\color{#ec0000}{\dfrac{\color{black}{8x}}{8}}\\24&=x\end{align}|| -
Répondre à la question
La largeur est de |24\ \text{cm},| alors que la longueur est de |72\ \text{cm}| |(3x = 3\times 24=72).|
Le Grand Prix Cycliste, qui se déroule depuis quelques années dans les villes de Québec et de Montréal, demande aux organisateurs de créer de nouveaux trajets tout en respectant certaines contraintes.
Cette année, la boucle à parcourir doit avoir une longueur de |15\ 000\ \text{m}| et doit être composée de différentes sections dont une montée, une descente et une ligne droite pour le sprint final.

Afin de respecter les standards entre les courses, la descente doit être 2 fois plus longue que la montée et la ligne droite pour le sprint doit être |300\ \text{m}| de plus que la moitié de la montée.
Quelle est la distance à parcourir pour chacune de ces 3 sections?
-
Déterminer la formule
On connait la longueur totale du parcours.
||\text{Longueur de la boucle}=\text{Somme de tous les segments}||
-
Remplacer les variables par les valeurs connues
Il manque plusieurs informations. On peut utiliser l’image pour s’aider à déterminer la longueur de la montée, de la descente et du sprint à l’aide de l’algèbre. On associe |\color{#3a9a38}x| à la longueur de la montée. Ainsi, l’expression algébrique qui représente la descente est |\color{#3b87cd}{2x}| et celle qui représente le sprint est |\color{#fa7921}{\dfrac{x}{2}+300}.|
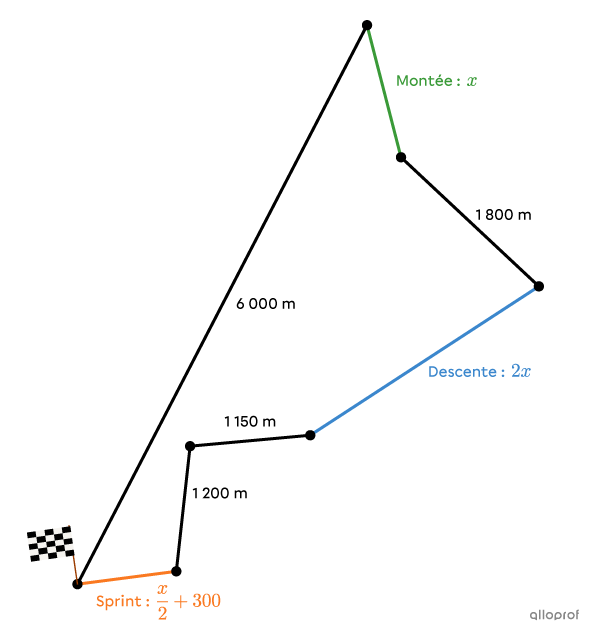
En remplaçant ces informations dans la formule de la longueur de la boucle, on obtient ceci.
||15\ 000=6\ 000+x+1\ 800+2x+1\ 150+1\ 200+\left(\dfrac{x}{2}+300\right)||
-
Isoler la variable recherchée
||\begin{align}15\ 000&=6\ 000+x+1\ 800+2x+1\ 150+1\ 200+\dfrac{x}{2}+300\\15\ 000&=\dfrac{7x}{2}+10\ 450\\15\ 000\color{#ec0000}{-10\ 450}&=\dfrac{7x}{2}+10\ 450\color{#ec0000}{-10\ 450}\\4\ 550&=\dfrac{7x}{2}\\4\ 550\color{#ec0000}{\times 2}&=\dfrac{7x}{2}\color{#ec0000}{\times 2}\\9\ 100&=7x\\\color{#ec0000}{\dfrac{\color{black}{9\ 100}}{7}}&=\color{#ec0000}{\dfrac{\color{black}{7x}}{7}}\\1\ 300&=x\end{align}||
-
Répondre à la question
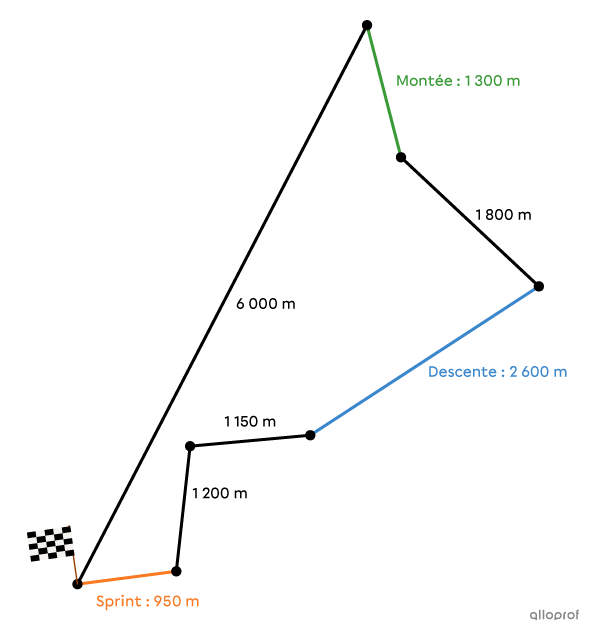
Ainsi, la montée a une longueur de |1\ 300\ \text{m},| la descente a une longueur de |2\ 600\ \text{m}| |(2x= 2\times 1\ 300=2\ 600)| et le sprint a une longueur de |950\ \text{m}| |\left(\dfrac{x}{2}+300=\dfrac{1\ 300}{2}+300=950\right).|
Pour valider ta compréhension des mesures manquantes dans les figures planes de façon interactive, consulte la MiniRécup suivante :
