Lorsqu’on ajoute les paramètres |a,| |b,| |h| et |k| à la forme de base |f(x)=(c)^x,| on obtient ce qu'on appelle la forme canonique (aussi appelée forme transformée) de la fonction exponentielle.
La forme canonique d'une fonction exponentielle est : ||f(x)=a(c)^{b(x–h)}+k||où |a,| |b,| |h| et |k| sont des nombres réels jouant le rôle de paramètres.
Remarque : Les paramètres |a,| |b| et |c| doivent être différents de zéro. De plus, la base |c| doit être supérieure à 0 et différente de 1.
Dans l'animation interactive suivante, tu peux modifier la valeur des paramètres |a|, |b|, |h|, |k| ainsi que celle de la base |c| de la fonction exponentielle. Observe bien les modifications qui s'opèrent sur la courbe transformée (en noir) par rapport à la fonction de base avec |c=2| (en bleu). Tu peux même en profiter pour observer l'effet de la modification des paramètres sur les propriétés de la fonction. Par la suite, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions sur chacun des paramètres.
Lorsque |\vert a \vert >1:|
La fonction exponentielle subit un étirement vertical par rapport à la fonction de base. En effet, plus la valeur absolue du paramètre |a| est grande, plus la courbe de la fonction exponentielle se rapproche de l’axe des |y.|
Lorsque |0< \vert a \vert <1:|
La fonction exponentielle subit une contraction verticale par rapport à la fonction de base. En effet, plus la valeur absolue du paramètre |a| est petite (près de 0), plus la courbe de la fonction exponentielle s'éloigne de l’axe des |y.|
Lorsque |a| est positif |(a>0):|
La courbe de la fonction exponentielle est tournée vers le haut, donc elle est croissante.
Lorsque |a| est négatif |(a<0):|
La courbe de la fonction exponentielle est tournée vers le bas, donc elle est décroissante.
Lorsque |\vert b \vert >1:|
La fonction exponentielle subit une contraction horizontale par rapport à la fonction de base. En effet, plus la valeur absolue du paramètre |b| est grande , plus la branche du graphique de la fonction exponentielle s'éloigne de l’axe des |x|.
Lorsque |0< \vert b \vert <1:|
La fonction exponentielle subit un étirement horizontal par rapport à la fonction de base. En effet, plus la valeur absolue du paramètre |b| est petite (près de 0), plus la branche du graphique de la fonction exponentielle se rapproche de l’axe des |x|.
Lorsque |b| est positif |(b>0)| :
La courbe de la fonction exponentielle est croissante de la gauche vers la droite.
Lorsque |b| est négatif |(b<0)| :
La courbe de la fonction exponentielle est décroissante de la gauche vers la droite.
Le paramètre |c| détermine la variation de la fonction exponentielle.
Lorsque |c>1:|
La fonction exponentielle est croissante de la gauche vers la droite.
Lorsque |0 < c < 1 :|
La fonction exponentielle est décroissante de la gauche vers la droite.
Lorsque |h| est positif |(h>0):|
La courbe de la fonction exponentielle se déplace vers la droite.
Lorsque |h| est négatif |(h<0):|
La courbe de la fonction exponentielle se déplace vers la gauche.
Pour bien identifier la valeur du paramètre |h|, il est important de se rappeler la définition même de la forme canonique d'une équation. Par exemple, |h(x)=2^{x+2}| contient un paramètre |h| dont la valeur est |h=-2.|
Lorsque |k| est positif |(k>0)| :
La courbe de la fonction exponentielle se déplace vers le haut.
Lorsque |k| est négatif |(k<0)| :
La courbe de la fonction exponentielle se déplace vers le bas.
Le paramètre |k| donne l'emplacement de l'asymptote de la fonction exponentielle.
L'équation de l'asymptote est |y=k|.
Si |c>1:|
| |a>0| | |a<0| | |
|---|---|---|
| |b>0| | 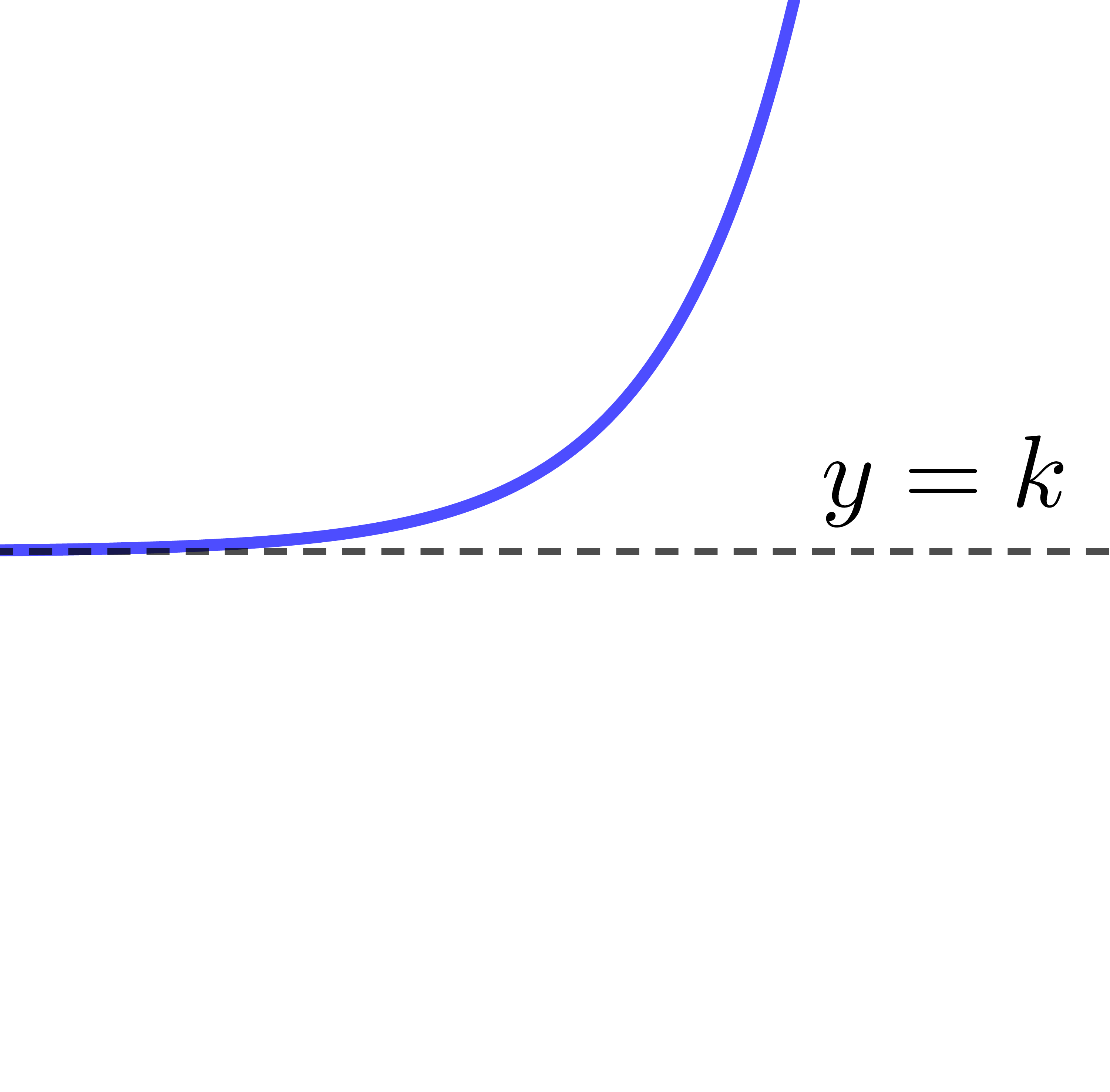 |
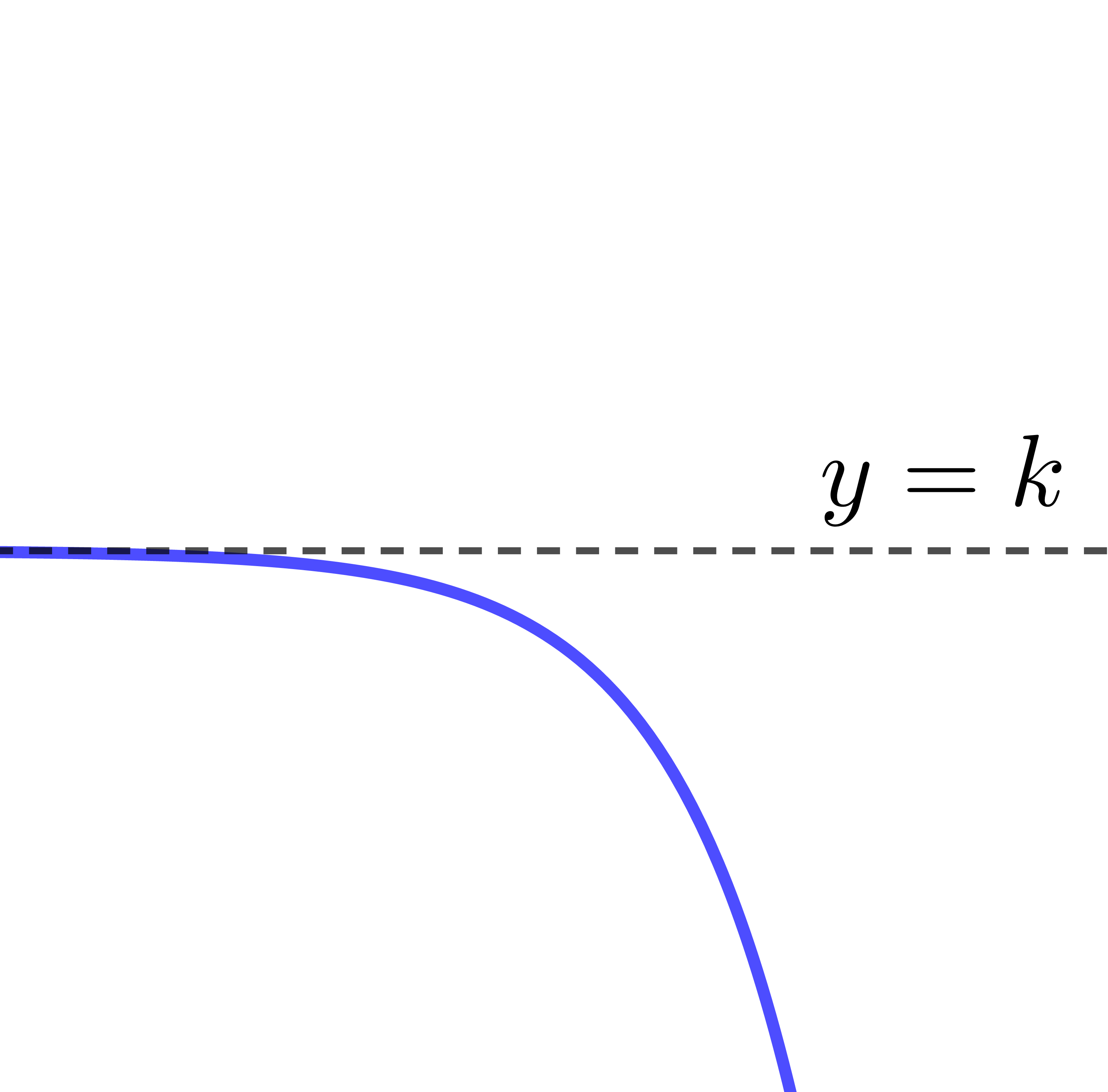 |
| |b<0| | 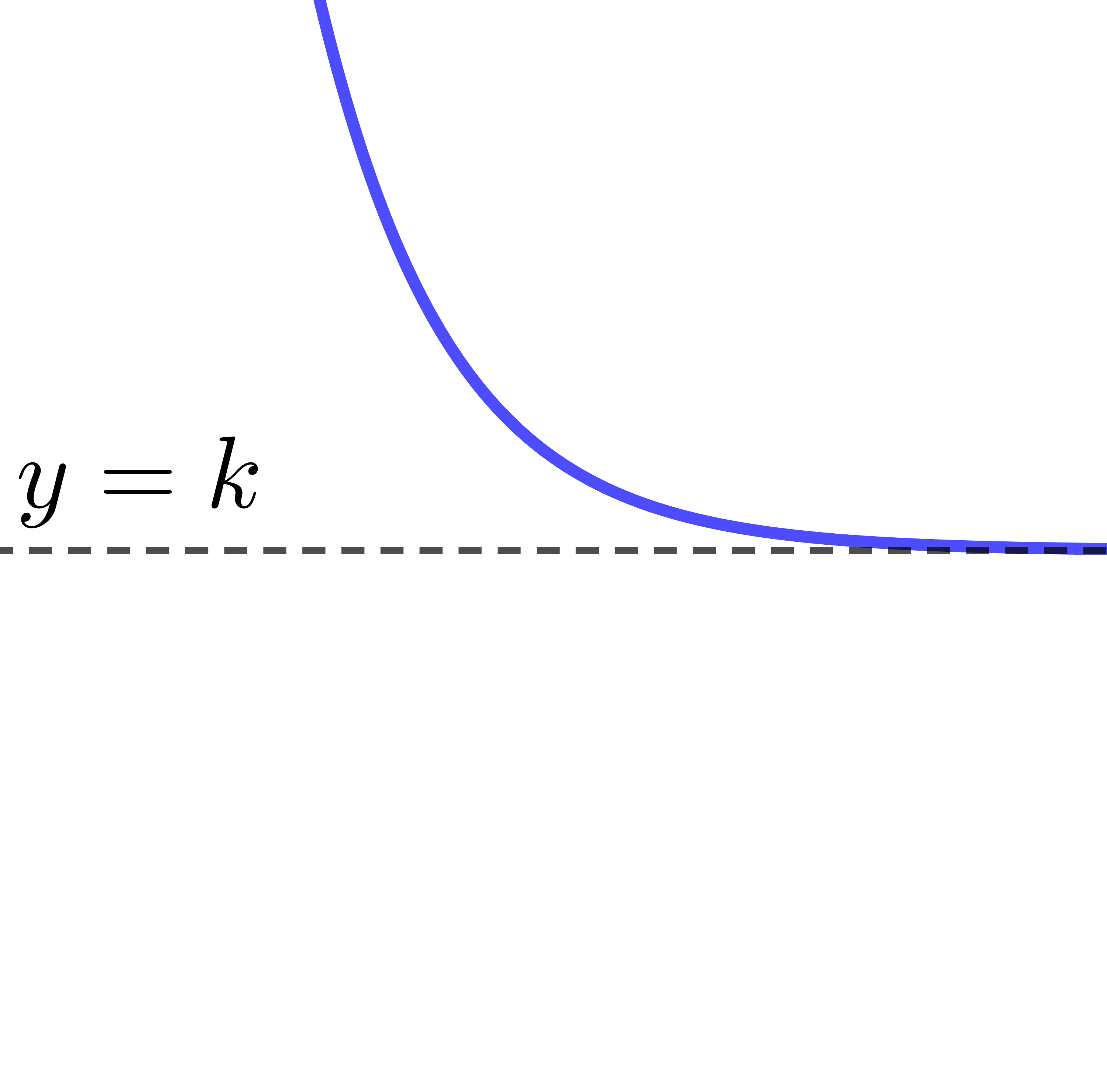 |
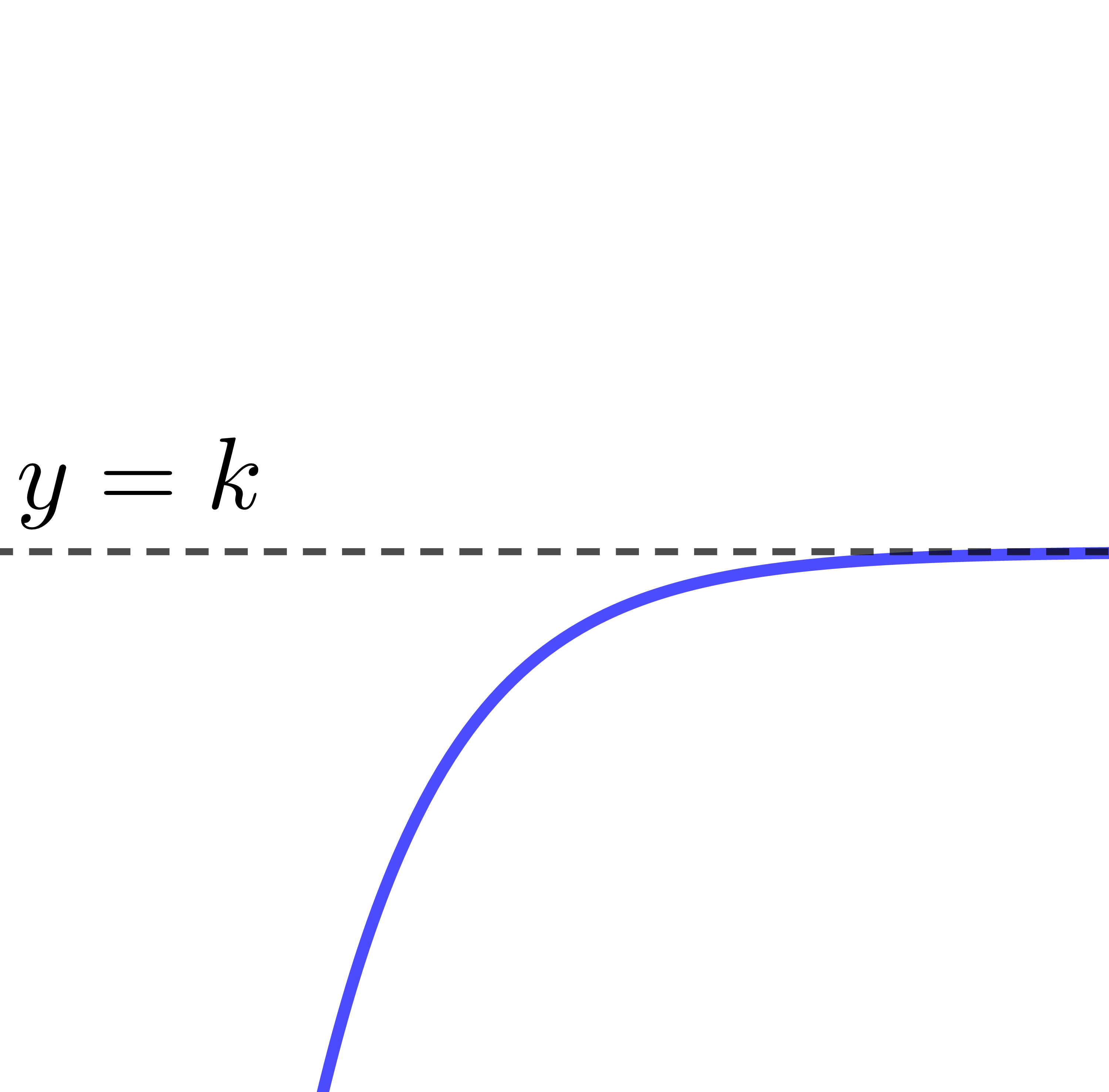 |
Si |0<c<1:|
| |a>0| | |a<0| | |
|---|---|---|
| |b>0| |  |
 |
| |b<0| |  |
 |
Comme tu peux le voir en observant le tableau-résumé ci-haut, certaines combinaisons des valeurs des paramètres et de la base donnent le même résultat. Par exemple, |c>1|, |a>0| et |b>0| est équivalent à |0<c<1|, |a>0| et |b<0|. C'est pour cette raison qu'on simplifie souvent l'équation d'une fonction exponentielle en forme canonique en éliminant les paramètres |b| et |h|. ||\large{f(x)=a(c)^{b(x-h)}+k \ \ \ \Rightarrow \ \ \ f(x)=a(c)^x+k}|| Pour cette façon simplifiée d'écrire la règle d'une fonction exponentielle, le tableau-résumé sera :
| |a>0| | |a<0| | |
|---|---|---|
| |c>1| |  |
 |
| |0<c<1| |  |
 |