La famille des fonctions exponentielles regroupe les fonctions pour lesquelles la variable indépendante |\boldsymbol{(x)}| est un exposant.
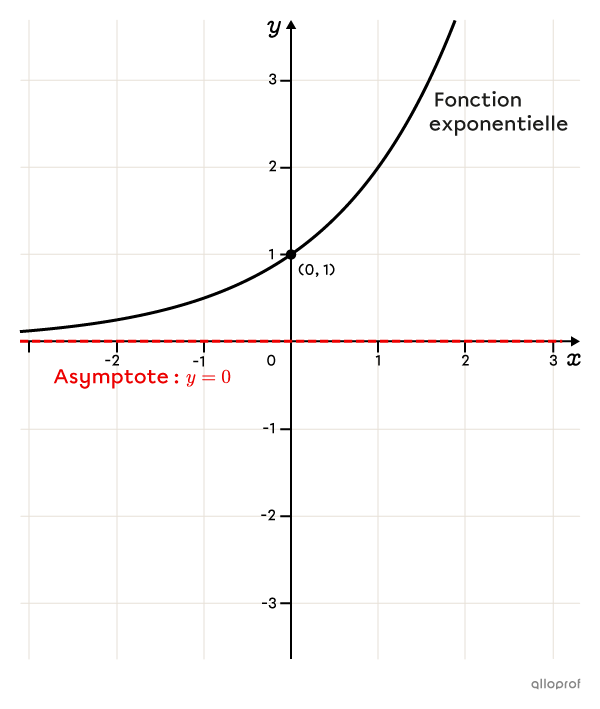
Toutes les fonctions exponentielles possèdent une asymptote. Graphiquement, cela signifie que les fonctions exponentielles sont représentées par une courbe qui se rapproche d’une droite horizontale sans jamais la croiser.
La fonction exponentielle peut être présentée sous l’une des formes suivantes.
La forme de base||f(x)=c^x||
Les formes canoniques simplifiées||f(x)=a(c)^x||ou||f(x)=a(c)^{bx}||
La forme canonique||f(x)=a(c)^{b(x-h)}+k||
La base |(c)| d’une fonction exponentielle est toujours un nombre supérieur à |0| et différent de |1.|
La fonction exponentielle est généralement présentée sous l’une des 2 formes suivantes.
||f(x)=a(c)^x||
||f(x)=a(c)^{bx}||
La règle d’une fonction exponentielle écrite avec les paramètres |a,| |b| et |c| peut toujours être simplifiée en une règle qui ne contient que les paramètres |a| et |c.| Voici la démonstration algébrique.||\begin{align}y&=a(c)^{bx}\\[3pt]&=a\left(\boldsymbol{\color{#3a9a38}{c^b}}\right)^x\\[3pt]&=a(\color{#7cca51}{\textbf{c}})^x\end{align}||Autrement dit, toute équation de la forme |y=a(c)^{bx}| est équivalente à une autre équation de la forme |y=a(\text{c})^x.|
Les fonctions |y=24(2)^{3x}| et |y=24(8)^x| sont équivalentes. En voici la preuve.||24(2)^{3x}=24\left(\boldsymbol{\color{#3a9a38}{2^3}}\right)^x=24(\boldsymbol{\color{#7cca51}{8}})^x||
Lorsqu’on veut trouver la règle d’une fonction exponentielle, il est préférable de la chercher sous la forme |y=a(\text{c})^x.| Cela évite d’avoir à chercher la valeur du paramètre |b.|
Une fonction exponentielle simplifiée possède toujours les caractéristiques suivantes.
-
Une asymptote dont la règle est |y=0|
-
Aucune abscisse à l’origine (zéro)
-
Une ordonnée à l’origine dont les coordonnées sont |(0,a)|
Dans l’animation interactive suivante, on peut déplacer les curseurs pour observer le rôle des paramètres |a,| |b| et |c.|
La fonction exponentielle sous la forme canonique est la suivante.
||f(x)=a(c)^{b(x-h)}+k||
La règle d’une fonction exponentielle sous la forme canonique peut toujours être simplifiée en une règle qui ne contient que les paramètres |a,| |c| et |k.| Voici la démonstration algébrique.||\begin{align}y&=a(c)^{b(x-h)}+k\\[3pt]&=a\left(\boldsymbol{\color{#3a9a38}{c^b}}\right)^{x-h}+k\\[3pt]&=a(\color{#7cca51}{\textbf{c}})^{x-h}+k\\[3pt]&=a\dfrac{\text{c}^x}{\text{c}^h}+k\\[3pt]&=\boldsymbol{\color{#3b87cd}{\dfrac{a}{\textbf{c}^h}}}\text{c}^x+k\\[3pt]&=\color{#51b6c2}{\textbf{a}}(\text{c})^x+k\end{align}||Autrement dit, toute équation de la forme |y=a(c)^{b(x-h)}+k| est équivalente à une autre équation de la forme |y=\text{a(c)}^x+k.|
Les fonctions |y=24(2)^{3(x-1)}+7| et |y=3(8)^x+7| sont équivalentes. En voici la preuve.||\begin{align}24(2)^{3(x-1)}+7&=24\left(\boldsymbol{\color{#3a9a38}{2^3}}\right)^{x-1}+7\\[3pt]&=24(\boldsymbol{\color{#7cca51}{8}})^{x-1}+7\\[3pt]&=24\dfrac{8^x}{8^1}+7\\[3pt]&=\boldsymbol{\color{#3b87cd}{\dfrac{24}{8}}}8^x+7\\[3pt]&=\boldsymbol{\color{#51b6c2}{3}}(8)^x+7\end{align}||
Lorsqu’on veut trouver la règle d’une fonction exponentielle, il est préférable de la chercher sous la forme |y=\text{a(c)}^x+k.| Cela évite d’avoir à chercher la valeur des paramètres |h| et |b.|
Une fonction exponentielle canonique possède toujours les caractéristiques suivantes.
-
Une asymptote dont l’équation est |y=k|
-
Une abscisse à l’origine (zéro) si |k\ne0|
-
Une ordonnée à l’origine
Dans l’animation interactive suivante, on peut déplacer les curseurs pour observer le rôle des paramètres |a,| |b,| |c,| |h| et |k.|