Dans le cas du taux d'intérêt composé, il permet de faire fructifier ses avoirs de façon plus rapide.
Un taux d'intérêt écrit en notation décimale, et noté |i|, est dit composé si l'intérêt est calculé en fonction du montant initial en plus des intérêts accumulés à la fin de chaque période de capitalisation.
Ainsi, le montant sur lequel est appliqué le taux d'intérêt augmentera de plus en plus rapidement avec le temps. En d'autres mots, le tout peut se représenter par un modèle exponentiel.
Si un montant de |1\ 000\ \$| est placé à un taux d'intérêt de |3\ \%| composé annuellement sur une durée de |5| ans, on obtiendra le rendement suivant.
| Nombre d'années écoulées | Rendement annuel ($) | Capital ($) |
|---|---|---|
| |0| | - | |1\ 000| |
| |1| | |3\ \%| de |1 \ 000 = 30| | |1\ 000 + 30 = 1 \ 030| |
| |2| | |3\ \%| de |1 \ 030 = 30{,}90| | |1 \ 030 + 30{,}90 = 1\ 060{,}90| |
| |3| | |3\ \%| de |1 \ 092{,}73 \approx 31{,}83| | |1 \ 060{,}90 + 31{,}83 = 1 092{,}73| |
| |4| | |3\ \%| de |1 \ 092{,}73 \approx 32{,}78| | |1 \ 092{,}73 + 32{,}78 = 1 \ 125{,}51| |
| |5| | |3\ \%| de |1 \ 125{,}51 \approx 33{,}77| | |1 \ 125{,}51 + 33{,}77 = 1 \ 159{,}28| |
Ainsi, le montant récolté après |5| années sera d'environ |1\ 159{,}28\ \$.|
En guise de rappel, ce type de modélisation fait référence à la fonction exponentielle. Financièrement parlant, cela signifie que les intérêts sont toujours calculés sur la capitalisation obtenue de la période d'intérêt précédente.
Non seulement le taux d'intérêt est annuel, mais il arrive souvent que la période d'intérêt se chiffre également en années. En d'autres mots, cela implique que les intérêts ne sont calculés qu'une fois par année.
Quelle est la représentation graphique d'un placement de |\color{#ec0000}{3\ 000 \ \$}| avec un taux d'intérêt composé de |3{,}25\ \%| sur une période de |2| ans?
-
Calculer le montant d'intérêt obtenu à chaque période d'intérêt
||\begin{align}\begin{gathered}\text{Temps écoulé}\\ \text{(années)}\end{gathered} &\ \begin{gathered}\text{Valeur du} \\ \ \ \text{ placement}\ (\$)\end{gathered} \\[5pt]0\qquad \ &\qquad\ \ \color{#ec0000}{3\ 000} \\&&&\!\!\!\!\!\!\!\!\!\! +3{,}25\ \%\ \text{de}\ 3\ 000=\color{#3b87cd}{97{,}50} \\1\qquad \ &\qquad\ \ 3\ 097{,}50 \\&&&\!\!\!\!\!\!\!\!\!\!+3{,}25\ \%\ \text{de}\ 3\ 097{,}50\approx\color{#3b87cd}{100{,}67} \\2\qquad \ &\qquad\ \ 3\ 198{,}17\end{align}||
-
Construire le graphique
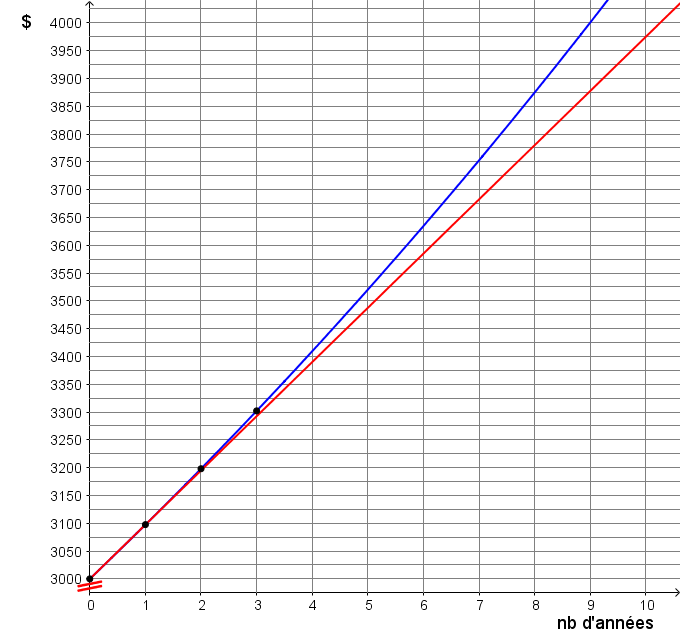
Dans l'exemple précédent, la ligne droite rouge représente un calcul d'intérêt simple. Par contre, la ligne courbe bleue représente un calcul d'intérêt composé. De cette façon, on peut voir que la capitalisation d'intérêt composé donne une plus grande capitalisation à long terme.
En utilisant l'exemple précédent, on peut déduire la règle d'une telle représentation graphique.
||C_n=C_0 \ \left(1+i \right)^n||
où
|C_n :| Valeur future (Capital accumulé)
|C_0 :| Valeur actuelle (Capital initial)
|i :| Taux d'intérêt composé annuel en notation décimale
|n :| Nombre de périodes d'intérêt (Durée)
Pour comprendre son origine, on doit utiliser la factorisation et la notation exponentielle.
|\begin{align} 3\ 198{,}17 &= \underbrace{\color{#3b87cd}{3\ 000}}_{\text{Valeur actuelle}} + \underbrace{\color{#3b87cd}{3\ 000 \times 0{,}032\,5}}_{\text{Intérêts après 1 an}} + \underbrace{(3\ 000+3\ 000\times 0{,}032\,5)\times 0{,}032\,5}_{\text{Intérêts après 2 ans}} \\ &= \underbrace{\color{#3b87cd}{3\ 000 (1 + 0{,}032\,5)}}_{\text{Mise en évidence de 3 000}} + (3\ 000 + 3\ 000 \times 0{,}032\,5) \times 0{,}032\,5\\ &= \color{#3b87cd}{3\ 000 (1 + 0{,}032\,5)}+ \underbrace{(\color{#3b87cd}{3\ 000 (1 + 0{,}032\,5)})}_{\text{Mise en évidence de 3 000}} \times 0{,}032\,5 \\ &= \underbrace{\color{#3b87cd}{3\ 000 (1 + 0{,}032\,5)}}_{\text{Mise en évidence}} (1+0{,}032\,5)\\ 3\ 198{,}17&= 3\ 000\!\! \underbrace{(1 + 0{,}032\,5)^2}_{\text{Définition de l'exposant}}\end{align}|
En généralisant, on obtient la règle.
|\qquad C_n = C_0 \ \left(1 + i \right)^n|
Une fois la règle trouvée, on peut l'utiliser pour calculer la capitalisation suite à une période précise.
Quelle serait la valeur future d'un placement de |\color{#ec0000}{3\ 000 \ \$}| avec un taux d'intérêt annuel composé de |\color{#3b87cd}{3{,}25\ \%}| sur une période de |\color{#ff55c3}{10}| ans?
-
Trouver la règle||\begin{align}C_n &= \color{#ec0000}{C_0} \ \left(1 + \color{#3b87cd}{i} \right)^ \color{#ff55c3}{n} \\ &= \color{#ec0000}{3\ 000} \ \left(1 + \color{#3b87cd}{0{,}032\,5} \right)^\color{#ff55c3}{n}\end{align}||
-
Calculer la valeur future selon la période donnée||\begin{align}C_n &= 3\ 000 \ \left(1 + 0{,}032\,5\right)^\color{#ff55c3}{n}\\ &= 3\ 000 \ \left(1{,}032\,5 \right)^\color{#ff55c3}{10} \\ &\approx 3\ 000 (1{,}376\ 89) \\ &\approx 4\ 130{,}68 \end{align}||
-
Interpréter la réponse
Après une période de |10| ans, la valeur actuelle |C_0 = 3\ 000\ \$| est devenue une valeur future |C_n\approx 4\ 130{,}68\ \$.|
En ce qui concerne la formule utilisée pour calculer la valeur future, il s'agit simplement de diviser le taux d'intérêt annuel selon la période d'intérêt donnée.
De façon générale, les termes suivants sont utilisés pour définir les différentes périodes d'intérêt.
|
Période |
Définition |
Fraction d'une année |
|---|---|---|
|
Quotidienne |
Une fois par jour |
|\dfrac{1}{365}| |
|
Hebdomadaire |
Une fois par semaine |
|\dfrac{1}{52}| |
|
Mensuelle |
Une fois par mois |
|\dfrac{1}{12}| |
|
Trimestrielle |
Une fois tous les 3 mois |
|\dfrac{1}{4}| |
|
Semestrielle |
Une fois tous les 6 mois |
|\dfrac{1}{2}| |
Il arrive que les taux d'intérêts soient en lien avec ces périodes. Il faudra donc porter une attention particulière aux nombres de périodes d'intérêts (durée) lors des calculs.
Quelle serait la valeur future d'un placement de |\color{#ec0000}{5\ 000\ \$}| avec un taux d'intérêt composé trimestriel de |\color{#3b87cd}{1{,}5\ \%}| sur une période de |\color{#ff55c3}{5}| ans?
-
Trouver la règle||\begin{align}C_n &= \color{#ec0000}{C_0} \ \left(1 + \color{#3b87cd}{i} \right)^\color{#ff55c3}{n} \\ &= \color{#ec0000}{5\ 000} \ \left(1 + \color{#3b87cd}{0{,}015} \right)^\color{#ff55c3}{n}\end{align}||
-
Déterminer le nombre de périodes d'intérêt||\begin{align} \begin{gathered}\text{trimestriel}\\ \text{pendant 5 ans}\end{gathered} &=\begin{gathered} \text{4 fois par année}\\ \text{pendant 5 ans}\end{gathered}\\[3pt] &= 4 \times 5 \\ &= 20\end{align}||
-
Calculer la valeur future selon la période donnée||\begin{align}C_n &= 5\ 000 \ \left(1 + 0{,}015 \right)^\color{#ff55c3}{n}\\ &= 5\ 000 \ \left(1 + 0{,}015 \right)^\color{#ff55c3}{20}\\ &= 5\ 000 \ \left (1{,}015 \right)^{20} \\ &\approx 6\ 734{,}28 \end{align}||
-
Interpréter la réponse
Après une période de |5| ans, la valeur actuelle |C_0 = 5\ 000\ \$| est devenue une valeur future |C_n\approx 6\ 734{,}28\ \$.|
Parfois, les taux d'intérêt en lien avec ces périodes sont calculés selon le taux annuel en vigueur. Même si la période d'intérêt est modifiée, la formule pour déterminer la valeur future ne subit qu'une légère modification.||C_n=C_0 \ \left(1+\frac{i}{k}\right)^n||
où
|C_n :| Valeur future (Capital accumulé)
|C_0 :| Valeur actuelle (Capital initial)
|i :| Taux d'intérêt composé annuel en notation décimale
|k :| Facteur en lien avec la période d'intérêt
|n :| Nombre de périodes d'intérêt (Durée)
Toujours en se référant au vocabulaire en lien avec les périodes d'intérêt, on s'aperçoit que cette dernière a un effet considérable sur la valeur future avec un intérêt composé.
Voici un exemple de l'application de cette formule.
Quelle serait la valeur future d'un placement de |\color{#ec0000}{3\ 000 \ \$}| avec un taux d'intérêt annuel composé de |\color{#3b87cd}{3{,}25\ \%}| sur une période de |\color{#ff55c3}{10}| ans avec une période d'intérêt mensuelle?
-
Trouver la règle||\begin{align} C_n &= \color{#ec0000}{C_0} \ \left(1 + \dfrac{\color{#3b87cd}{i}}{\color{#fa7921}{k}} \right)^\color{#ff55c3}{n} \\ &= \color{#ec0000}{3\ 000} \ \left(1 + \dfrac{\color{#3b87cd}{0{,}032\,5}}{\color{#fa7921}{12}} \right)^\color{#ff55c3}{n}\end{align}||
-
Déterminer le nombre de périodes d'intérêt||\begin{align} \begin{gathered}\text{mensuelle}\\ \text{pendant 10 ans}\end{gathered} &=\begin{gathered} \text{12 fois par année}\\ \text{pendant 10 ans}\end{gathered}\\[3pt] &= 12 \times 10 \\ &= 120\end{align}||
-
Calculer la valeur future selon la période donnée||\begin{align}C_n &= 3\ 000 \ \left(1 + \dfrac{0{,}032\,5}{12} \right)^\color{#ff55c3}{n}\\ &= 3\ 000 \ \left(1 + \dfrac{0{,}032\,5}{12} \right)^\color{#ff55c3}{120}\\ &\approx 3\ 000 \ \left (1{,}002\,7 \right)^{120} \\ &\approx 4\ 150{,}27 \end{align}||
-
Interpréter la réponse
Après une période de |10| ans, la valeur actuelle |C_0 = 3\ 000\ \$| est devenue une valeur future |C_n\approx 4\ 150{,}27\ \$.|
Dans certains cas, les investisseurs vont effectuer des placements dans le but d'obtenir un montant final précis. En d'autres mots, la valeur future (capital accumulé) ainsi que la durée du placement (nombre de périodes) sont connues alors que la valeur actuelle (capital initial) est inconnue. Il s'agit de l'opération inverse de la capitalisation.
Puisque c'est la valeur actuelle (capital initial) que l'on cherche, il est alors question d'actualisation.
Avec la notion d'intérêt composé, les manipulations algébriques deviennent un peu plus complexes. En effet, la présence d'un exposant force l'utilisation des lois des exposants.
Tout comme pour résoudre n'importe quel type d'équations, on peut utiliser les opérations inverses pour isoler une variable.
Avec la naissance de son 3e enfant, Vincent tient à mettre de l'argent de côté afin de payer les frais de scolarité de son garçon. Selon les informations disponibles, le cout moyen associé à des études universitaires est de |\color{#ec0000}{60 \ 000\ \$}.|
En prenant pour acquis que cette somme devra être disponible dans |\color{#ff55c3}{23}| ans, quel montant Vincent devrait-il placer si le plan qu'il utilise est basé sur un taux d'intérêt composé mensuel de |\color{#3b87cd}{0{,}2\ \%}|?
-
Trouver la règle||\begin{align} \color{#ec0000}{C_n} &= C_0 \ \left(1+{\color{#3b87cd}{i}} \right)^{\color{#ff55c3}{n}} \\ \color{#ec0000}{60 \ 000} &= C_0 \ \left(1+{\color{#3b87cd}{0{,}002}} \right)^{\color{#ff55c3}{12 \times 23}} \\ \color{#ec0000}{60 \ 000} &= C_0 \ \left(1+{\color{#3b87cd}{0{,}002}} \right)^{\color{#ff55c3}{276}}\end{align}||
-
Isoler la valeur actuelle (capital initial)||\begin{align} \color{#ec0000}{60\ 000} &= C_0 \ \left(1+{\color{#3b87cd}{0{,}002}} \right)^{\color{#ff55c3}{276}} \\ \color{#ec0000}{60\ 000} &= C_0 \ \left(1{,}002 \right)^{\color{#ff55c3}{276}} \\ \dfrac{\color{#ec0000}{60\ 000}}{\color{#3a9a38}{1{,}735\,8}} &\approx \dfrac{C_0 \left(1{,}735\,8 \right)}{\color{#3a9a38}{1{,}735\,8}} \\ 34 \ 566{,}87 &\approx C_0 \end{align}||
-
Donner la réponse dans une phrase
Ainsi, la valeur actuelle du placement de Vincent devrait être d'environ |34\ 566{,}87\ \$.|
Afin d'éviter les erreurs de calculs, on peut déduire une formule de cette procédure.
||C_0 = C_n \ \left(1+{i} \right)^{-n}||
où
|C_0 :| Valeur actuelle (Capital initial)
|C_n :| Valeur future (Capital accumulé)
|i :| Taux d'intérêt composé annuel en notation décimale
|n :| Nombre de périodes d'intérêt (Durée)
Ainsi, la démarche est plus concise.
Avec tous ses placements, Gitane a oublié le montant actuel d'un d'entre eux. Par contre, elle dispose des informations suivantes.
-
placement selon un taux d'intérêt composé hebdomadaire de |0{,}04\ \%|
-
placement d'une durée totale de |5| ans
-
valeur future (capital accumulé) obtenue : |4\ 660{,}23\ \$.|
Quel est la valeur actuelle (capital initial) de ce placement?
-
Identifier les différentes données||\begin{align} \color{#ec0000}{C_n} &= \color{#ec0000}{4\ 660{,}23} \\ \color{#3b87cd}{i} &= \color{#3b87cd}{0{,}04 \ \%} = \color{#3b87cd}{0{,}000\,4} \\ \color{#ff55c3}{n} &= \color{#ff55c3}{5 \times 52 = 260}\end{align}||
-
Appliquer la formule||\begin{align} C_0 &= {\color{#ec0000}{C_n}}{\left(1+{\color{#3b87cd}{i}}\right)^\color{#ff55c3}{-n}} \\ &= {\color{#ec0000}{4\ 660{,}23}}{\left(1+{\color{#3b87cd}{0{,}000\,4}}\right)^\color{#ff55c3}{-260}} \\ &\approx 4\ 200{,}00 \end{align}||
-
Donner la réponse dans une phrase
La valeur actuelle du placement de Gitane est d'environ |4\ 200{,}00\ \$.|
Tout comme plusieurs formules en mathématiques, cette dernière peut être démontrée à l'aide de quelques manipulations arithmétiques.
Comme pour la modélisation, l'actualisation peut être faite à partir de la formule suivante.
||C_n=C_0 \ \left(1+\dfrac{i}{k}\right)^n||
où
|C_n :| Valeur future (Capital accumulé)
|C_0 :| Valeur actuelle (Capital initial)
|i :| Taux d'intérêt composé annuel en notation décimale
|k :| Facteur en lien avec la période d'intérêt
|n :| Nombre de périodes d'intérêt (Durée)