Tout comme chacun des polyèdres réguliers convexes (solides de Platon), le tétraèdre régulier a des caractéristiques très particulières.
Le tétraèdre est une pyramide à base triangulaire.
Par contre, on parlera de tétraèdre régulier lorsque les faces de cette pyramide sont des triangles équilatéraux isométriques.
De par sa construction, il est possible d'en déduire d'autres caractéristiques
Pour s'assurer de respecter sa définition et sa construction, il est important de garder ces caractéristiques en mémoire:
Les caractéristiques du tétraèdre régulier sont les suivantes :
-
Deux arêtes ayant une extrémité commune forment un angle de |60^\circ|
-
Les quatre faces sont des triangles équilatéraux isométriques
-
Les faces adjacentes forment des angles de |60^\circ|
En respectant chacune de ces propriétés, on obtient toujours le même genre de résultat.

Puisqu'il est particulier, on peut considérer le tétraèdre régulier comme faisant partie d'une classe à part. On peut non seulement calculer son aire et son volume en le considérant comme une pyramide, mais on peut également les calculer en ne possédant que la mesure d'une arête.
Bien entendu, les formules suivantes s'appliquent seulement aux tétraèdres réguliers et non à tous les tétraèdres.
||A_T = \sqrt{3}\, a^2||où
|a:| mesure d'une arête
De cette façon, les calculs pour déterminer son aire sont moins nombreux et la démarche est plus courte que pour les autres tétraèdres.
Quelle est l'aire totale de ce tétraèdre régulier?
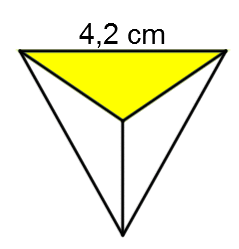
Puisqu'on mentionne que c'est un tétraèdre régulier, on peut utiliser la formule suivante.||\begin{align}A_T &= \sqrt{3}\, a^2\\
&= \sqrt{3}\, (4{,}2)^2\\
&\approx 30{,}55 \ \text{cm}^2\end{align}||
Par ailleurs, on peut faire le même constat avec le calcul du volume. Puisqu'il est question d'un tétraèdre régulier, il est possible de procéder de deux façons différentes. La première, en considèrant le tétraèdre régulier comme une pyramide à base triangulaire et en appliquant la démarche en lien avec les pyramides; la deuxième, en utilisant la formule suivante si on connaît la mesure d'une de ses arêtes.
||V = \dfrac{\sqrt{2}}{12}\, a^3||où
|a:| mesure d'une arête
En utilisant cette formule, la démarche est beaucoup plus courte et les risques d'erreur sont diminués.
Quel est le volume de ce tétraèdre régulier?
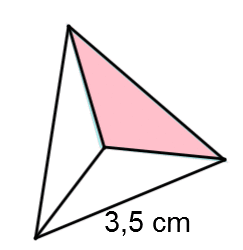
Puisqu'il est mentionné que c'est un tétraèdre régulier, on peut utiliser la formule suivante.||\begin{align}V &= \dfrac{\sqrt{2}}{12}\, a^3\\
&= \dfrac{\sqrt{2}}{12}\, (3{,}5)^3\\
&\approx 5{,}05\ \text{cm}^3\end{align}||
Malgré l'aspect pratique de ces deux formules, on peut les utiliser si et seulement si le polyèdre en question est un tétraèdre régulier. Dans le cas où il s'agirait d'un simple tétraèdre, il faudra le considérer comme une pyramide à base triangulaire et utiliser la méthode qui lui est associée.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><img alt="La Foire" data-entity-type="file" data-entity-uuid="ae991aa3-c455-40bc-a6b3-9d8898a8804b" src="/sites/default/files/inline-images/LaFoire_3.jpg"></p>
<p><a href="/fr/eleves/bv/jeux/la-foire">Accéder au jeu</a></p>
</body></html>