Like all regular convex polyhedra (Platonic solids), the regular tetrahedron has very specific characteristics.
A tetrahedron is a triangular-based pyramid.
However, when the faces of this pyramid are congruent equilateral triangles, it is called a regular tetrahedron.
Other characteristics can be deduced from its construction.
It is important to keep these characteristics in mind to ensure that its definition and construction are respected:
The characteristics of a regular tetrahedron are as follows:
-
Two edges with a common vertex form a |60^\circ| angle.
-
All four faces are congruent equilateral triangles.
-
Adjacent faces form |60^\circ| angles.
The result is always the same when these properties are respected.

Since they are a special case, regular tetrahedrons can be considered to be in a class of their own. Its area and volume can be calculated by treating it as a pyramid, but it can also be calculated using only the measure of one edge.
The following formulas apply only to regular tetrahedrons, and not to all tetrahedrons.
||A_T = \sqrt{3}\, a^2||where
|a|: length of one edge
This way, there are fewer calculations to find its area, and the process is shorter than for other tetrahedra.
What is the total area of this regular tetrahedron?
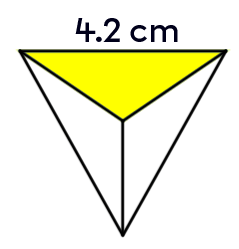
Since it is a regular tetrahedron, use the following formula:||\begin{align}A_T&=\sqrt{3}\,a^2\\&=\sqrt{3}\,(4.2)^2\\&\approx30.55\ \text{cm}^2\end{align}||
The same is true when it comes to calculating volume. Since it is a regular tetrahedron, there are two different possible approaches. The first is to consider the regular tetrahedron as a triangular pyramid and to apply the process related to pyramids; the second is to use the formula below if the length of one of its edges is known.
||V = \dfrac{\sqrt{2}}{12}\, a^3||where
|a:| length of one edge
This formula makes the process much shorter and reduces the risk of making mistakes.
What is the volume of this regular tetrahedron?
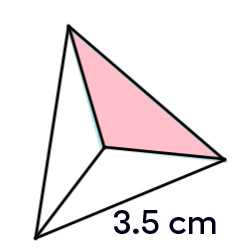
Since this is a regular tetrahedron, use the following formula:||\begin{align}V&=\dfrac{\sqrt{2}}{12}\,a^3\\&=\dfrac{\sqrt{2}}{12}\,(3.5)^3\\&\approx5.05\ \text{cm}^3\end{align}||
Despite the convenience of these two formulas, it is only possible to use them if and only if the polyhedron in question is a regular tetrahedron. Otherwise, it must be considered to be a triangular-based pyramid and its corresponding method must be used.