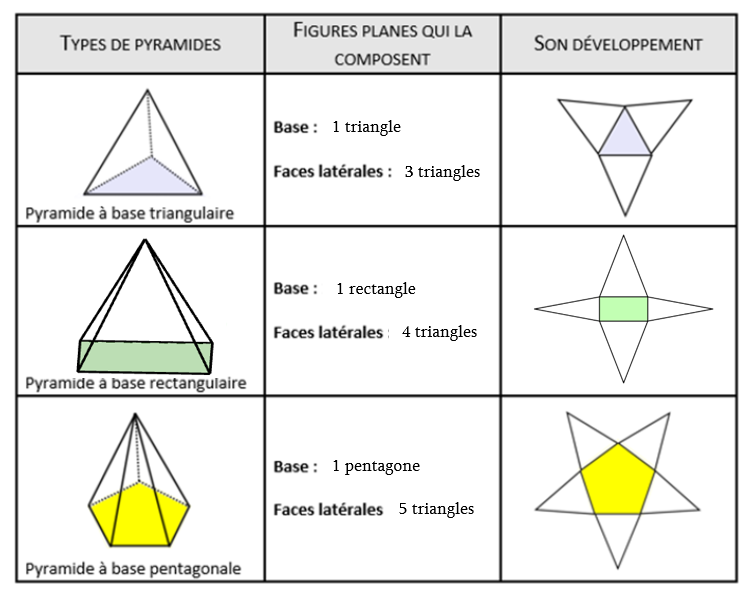
Le développement d'une pyramide est obtenu lorsque chacune de ses faces est dessinée sur une feuille et donc, sur le même plan. Une fois découpé, il suffit de plier les arêtes du dessin afin de former la pyramide.
Le développement d'une pyramide est une représentation en deux dimensions de sa base et de l'ensemble de ses faces latérales qui sont nécessairement des triangles.
De façon générale, on va s'efforcer de travailler avec des pyramides qui sont droites. En d'autres mots, on va chercher à ce que le sommet de la pyramide (l'apex) soit centré avec la base.
Il est facile de reconnaître le développement d'une pyramide: ses faces latérales sont toujours des triangles. Par ailleurs, la pyramide ne présente qu'une seule base qui peut prendre la forme de n'importe quel polygone. Plus précisément, si la base de la pyramide est un triangle équilatéral, elle portera le nom de tétraèdre.
Dans l'illustration ci-dessous, on peut voir la pyramide à son état initial et suivre son développement en quelques étapes
Une fois que le développement précédent est maîtrisé, il est plus facile de comprendre les développements des pyramides avec une base autre que carrée.
Afin de représenter une pyramide en trois dimensions, il est nécessaire de débuter avec la construction de sa base. Par la suite, on forme un premier triangle à partir d'un des côtés de la base. Finalement, on rejoint chaque sommet de la base à l'apex de la pyramide.
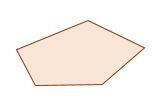
Étape 1 : On dessine la base en utilisant les outils de construction nécessaires. Il est possible de consulter la fiche suivante au besoin : la construction des figures planes.
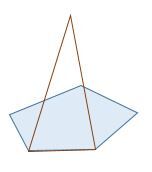
Étape 2 : On construit un premier triangle à partir de deux sommets consécutifs de la base.
Étape 3 : On relie chaque sommet de la base à l'apex formée par le premier triangle.
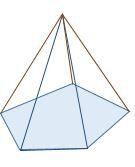
Finalement, il suffit de changer la base afin d'obtenir une pyramide d'une nature différente.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
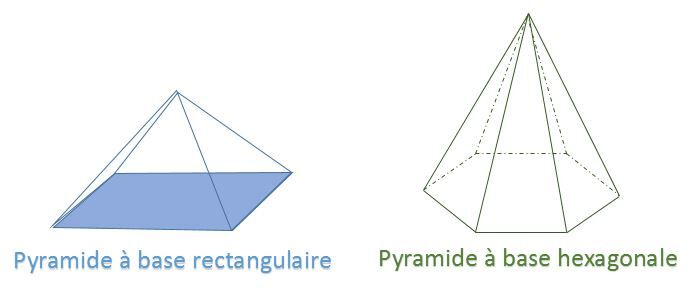
<html><body><p>Dans le cas de la pyramide à base rectangulaire, le rectangle ressemble plutôt à un parallélogramme. Or, c'est <a href="/fr/eleves/bv/mathematiques/les-projections-et-les-perspectives-m1274">l'effet de perspective</a> du dessin en trois dimensions qui cause cette distorsion.</p>
</body></html>