Avant toute chose, il faut être en mesure de reconnaitre les différentes parties d’une pyramide pour bien l’identifier : les figures qui constituent la base et les faces latérales ainsi que la hauteur de la pyramide. Une fois cette étape accomplie, on peut entreprendre le calcul de son aire.
Comme la pyramide peut avoir n'importe quel polygone comme base, il est nécessaire de bien l'identifier afin de pouvoir déterminer la manière dont on calcule son aire, identifiée |A_b.| Ainsi, il est nécessaire de se référer aux formules de calcul de l’aire des figures planes afin de connaitre celle qu’il faut utiliser selon le type de polygone qui forme la base de la pyramide.
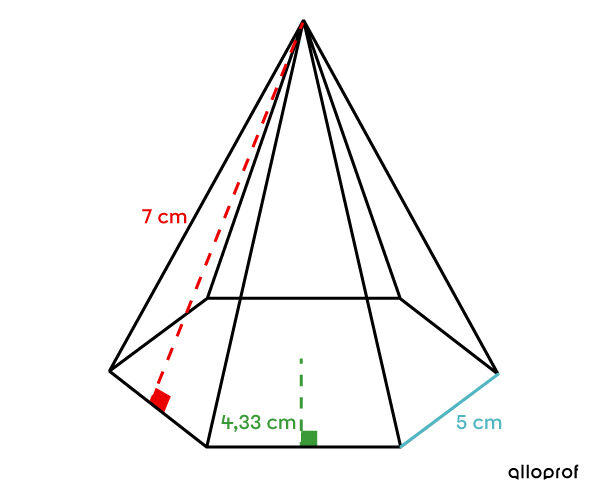
Quelle est l'aire de la base de la pyramide régulière suivante?
-
Identifier la face concernée
Dans cet exemple, la base est un hexagone régulier. -
Appliquer la formule appropriée
Puisque cette figure plane fait partie des polygones réguliers, on applique la formule : ||\begin{align} A_b &=A_{\text{polygones réguliers}}\\\\&= \dfrac{\color{#51B6C2}{c} \times \color{#3A9A38}{a_b} \times n}{2}\\\\&= \dfrac{\color{#51B6C2}{5} \times \color{#3A9A38}{4{,}33} \times 6}{2}\\\\&= 64{,}95 \ \text{cm}^2 \end{align}|| -
Interpréter la réponse
Puisqu'il n'y a aucun contexte qui entoure le problème, on affirme simplement que l'aire de la base de cette pyramide est de |64{,}95\ \text{cm}^2.|
Dans le cas d’une pyramide régulière dont la base est un polygone régulier, il faut faire attention de ne pas confondre l’apothème de la base avec celui de la pyramide.
Comme l’apothème est généralement identifié par la variable |a,| il est suggéré de les différencier en y ajoutant un indice. Ainsi, l’apothème de la pyramide devient |a_p| et l’apothème de la base devient |a_b.| Le choix de l’indice ou de la façon d’identifier ces 2 mesures peut différer.
Pour calculer l’aire latérale d’une pyramide, il est important de savoir s’il s’agit d’une pyramide régulière ou non.
L’aire latérale d'une pyramide régulière
Dans les cas où le solide est une pyramide droite dont la base est un polygone régulier, les faces latérales sont des triangles isocèles isométriques.
||A_L = \dfrac{P_b \times a_p}{2}|| où ||\begin{align}A_L&:\text{Aire latérale}\\P_b&:\text{Périmètre de la base}\\a_p &: \text{apothème de la pyramide}\end{align}||
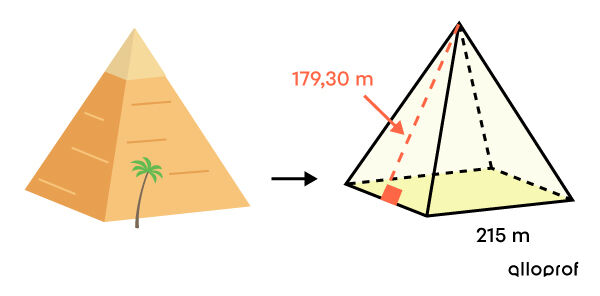
Afin de garder certaines des pyramides d'Égypte ouvertes au public, on doit restaurer leur façade. Pour préparer un appel d’offres en bonne et due forme aux différentes compagnies, on veut connaitre la superficie des surfaces à restaurer de la pyramide à base carrée de Khéphren.
-
Identifier le solide
Il s'agit d'une pyramide à base carrée. On cherche donc l’aire latérale d’une pyramide régulière. -
Appliquer la formule d'aire latérale du solide identifié ||\begin{align} A_L &=\dfrac{P_b \times \color{#FA7921}{a_p}}{2}\\\\&=\dfrac{(215+215+215+215) \times \color{#FA7921}{179{,}30}}{2}\\\\&= 77\ 099 \ \text{m}^2\end{align}||
-
Interpréter la réponse
La superficie des surfaces à restaurer équivaut à |77\ 099\ \text{m}^2.|
Remarque : La même réponse aurait été trouvée en calculant l'aire d'une face latérale (un triangle) et en la multipliant par 4 puisqu'il s'agit d'une pyramide à base carrée.
Afin de bien comprendre la formule, voici quelques explications supplémentaires.
Démonstration de la formule de l'aire latérale d'une pyramide régulière
-
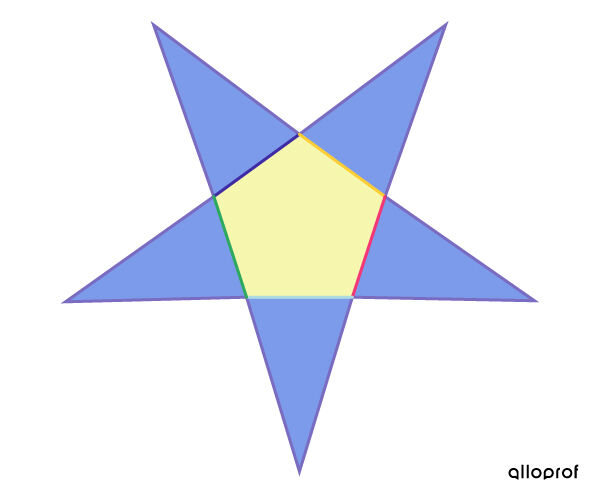
On fait le développement de la pyramide.
On peut associer la base de chaque triangle à un côté de la base de la pyramide.
-
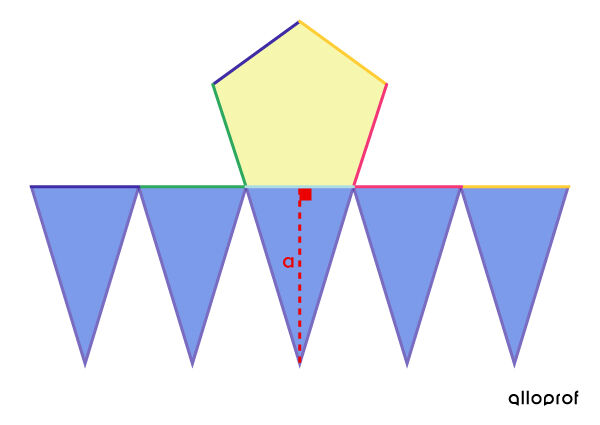
On place les triangles côte à côte.
-
On fait glisser les sommets de chacun des triangles pour qu’ils se rejoignent en un même point.
Ce qui est important ici, c’est que même si les triangles ont changé, l’aire de chacun des 5 triangles reste la même étant donné que leur base et leur hauteur ont conservé leur mesure. L’aire latérale de la pyramide est donc toujours la même.
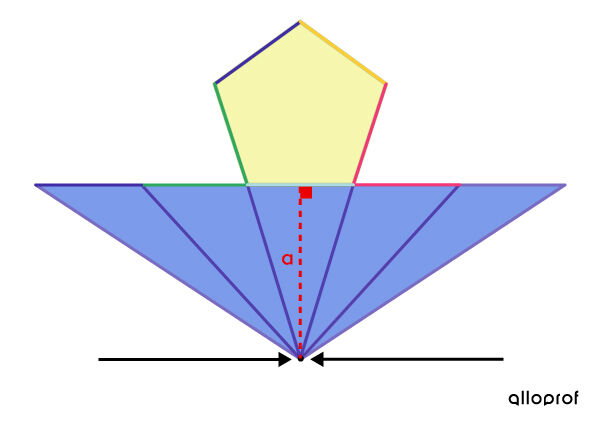
-
On voit que les 5 triangles en forment maintenant 1 seul dont l’aire se calcule avec la nouvelle base et avec la hauteur de l’un des triangles formant l’aire latérale.

On utilise donc la formule habituelle de l’aire d’un triangle, c’est-à-dire |A = \dfrac{b\times h}{2}.| Sur la figure, comme la base du grand triangle correspond au périmètre de la base, on remplace |b| par |P_b| et comme la hauteur du triangle correspond à l’apothème de la pyramide, on remplace |h| par |a.| Ainsi, on obtient la formule de l’aire latérale d’une pyramide régulière présentée plus haut. ||\begin{align} \color{#333FB1}{A_L} &= \text{Aire du grand triangle} \\ &= \dfrac{\color{#FA7921}b \times \color{#EC0000}{h}}{2} \\ &= \dfrac{\color{#FA7921}{P_b}\times \color{#EC0000}{a}}{2} \end{align}||
L’aire latérale d’une pyramide irrégulière
Il n’y a pas de formule pour l’aire latérale d’une pyramide irrégulière. Toutefois, il est possible de calculer l’aire latérale en décomposant les faces latérales en triangles. On doit alors calculer séparément l’aire de chacun des triangles et additionner le tout à la fin.
Calcule l’aire latérale de la pyramide rectangulaire suivante.
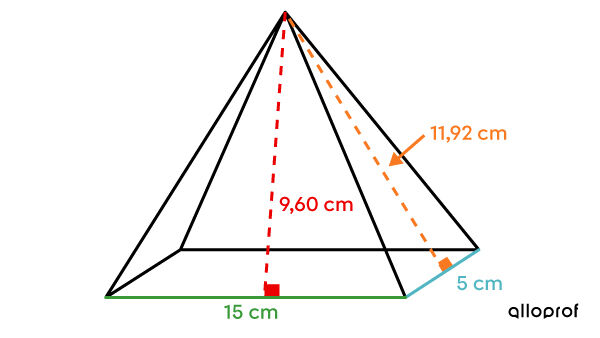
-
Identifier le solide
Il s'agit d'une pyramide à base rectangulaire. On ne peut donc pas utiliser la formule de l’aire latérale d’une pyramide régulière, il faut calculer les 4 faces latérales séparément. ||\begin{align} A_{\triangle\ \text{avant}} &= A_{\triangle\ \text{arrière}}= \dfrac{\color{#3A9A38}{b_1}\times \color{#EC0000}{h_1}}{2} \\\\ A_{\triangle\ \text{de droite}} &= A_{\triangle\ \text{de gauche}}= \dfrac{\color{#51b6c2}{b_2}\times \color{#FA7921}{h_2}}{2} \\\\ A_L &= 2\times A_{\triangle\ \text{avant}} + 2 \times A_{\triangle\ \text{de droite}}\end{align}|| -
Appliquer la formule d'aire latérale du solide identifié ||\begin{align} A_{\triangle\ \text{avant}} &= \dfrac{\color{#3A9A38}{15}\times \color{#EC0000}{{9{,}60}}}{2} \\ &= 72\ \text{cm}^2 \\\\ A_{\triangle\ \text{de droite}} &= \dfrac{\color{#51b6c2}{5}\times \color{#FA7921}{11{,}92}}{2} \\ &=29{,}8\ \text{cm}^2 \\\\ A_L &= 2\times A_{\triangle\ \text{avant}} + 2 \times A_{\triangle\ \text{de droite}} \\ &= 2 \times 72 + 2 \times 29{,}8 \\ &= 203{,}6\ \text{cm}^2 \end{align}||
-
Interpréter la réponse
L’aire latérale de la pyramide est de |203{,}6\ \text{cm}^2.|
L'aire totale d'une pyramide s'obtient en additionnant son aire latérale et l'aire de sa base.
||A_T = A_L + A_b|| où ||A_T: \text{Aire totale}||
Il s'agit surtout d'une combinaison des deux formules vues plus haut.
Pour recouvrir les dés en forme de tétraèdre régulier d'un jeu de Donjons et Dragons, on veut utiliser un matériau particulier pour assurer leur solidité.
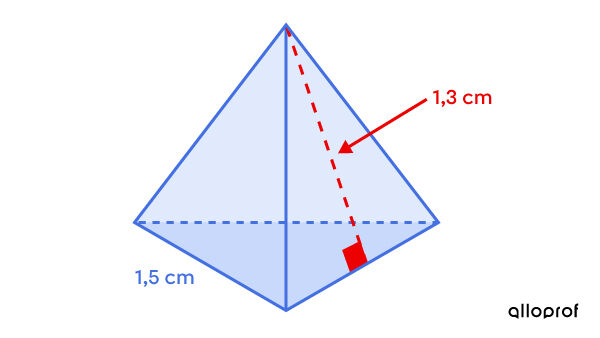
Si on veut recouvrir 150 de ces dés, quelle quantité de matériau sera nécessaire?
-
Identifier les faces concernées
Comme on recouvre entièrement les dés, on doit calculer la superficie des 4 faces, soit l’aire totale. -
Calculer l'aire de la base
Puisqu'il s'agit d'un tétraèdre régulier, toutes les faces sont des triangles équilatéraux isométriques. Ainsi, ||\begin{align} A_b &= \dfrac{\color{#3B87CD}b \times \color{#EC0000}h}{2} \\ &= \dfrac{\color{#3B87CD}{1{,}5} \times \color{#EC0000}{1{,}3}}{2} \\ &= 0{,}975 \ \text{cm}^2\end{align}|| -
Calculer l'aire latérale
Puisque le tétraèdre fait partie du groupe des pyramides régulières, ||\begin{align} A_L &= \dfrac{\color{#3b87cd}{P_b} \times \color{#ec0000}a}{2} \\ &= \dfrac{(\color{#3b87cd}{1{,}5} + \color{#3b87cd}{1{,}5} + \color{#3b87cd}{1{,}5}) \times \color{#ec0000}{1{,}3}}{2}\\ &= 2{,}925 \ \text{cm}^2\end{align}|| -
Calculer l'aire totale ||\begin{align} A_T &= A_L + A_b \\ &= 2{,}925 + 0{,}975\\ &= 3{,}9 \ \text{cm}^2 \end{align}||
-
Interpréter la réponse
Puisqu'on veut recouvrir 150 de ces dés, la superficie totale est de |3{,}9\ \text{cm}^2/\text{dé} \times 150\ \text{dés}= 585\ \text{cm}^2.|
Remarque : Comme le tétraèdre régulier est un solide particulier composé de 4 triangles équilatéraux, on peut aussi calculer son aire à l’aide de la formule suivante.
||A_T=4\times\dfrac{b\times h}{2}|| où ||\begin{align} b &: \text{arête ou base d’un triangle} \\ h &: \text{apothème ou hauteur d’un triangle} \\ A_T &: \text{Aire totale du tétraèdre} \end{align}||
Dans d'autres circonstances, on pourrait s'intéresser à la mesure d’une dimension de la base ou encore de l’apothème de la pyramide alors que l’aire totale est donnée, c’est ce qui s’appelle trouver une mesure manquante d'une pyramide à partir de l'aire. Dans ce cas, la démarche est un peu différente, mais il demeure essentiel de se rappeler la formule de l’aire totale associée aux pyramides.
Il n'y a pas de formule propre au calcul de la mesure de l’apothème dans une pyramide, mais on utilise généralement une formule très répandue dans le domaine des mathématiques : le théorème de Pythagore.
Trouver la mesure de l'apothème à partir de la hauteur
Dans le cas d'une pyramide droite, on peut obtenir un triangle rectangle en traçant l’apothème de la pyramide, la hauteur de la pyramide et le segment reliant le centre de la base et le milieu du côté de la base.
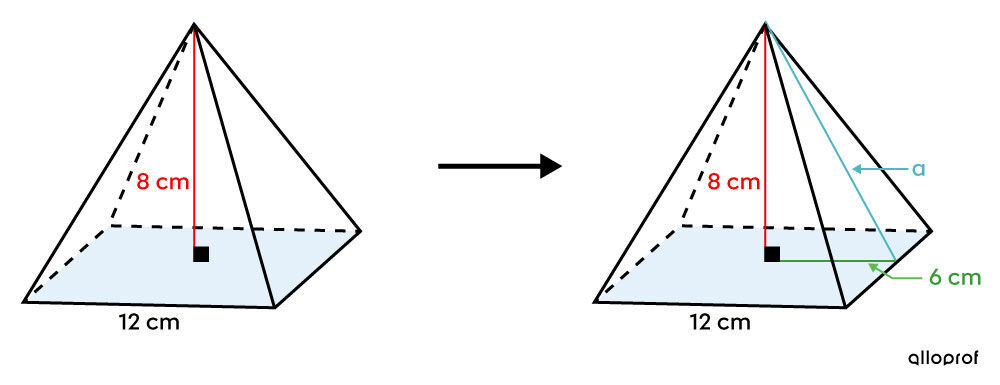
Puisque la hauteur est au centre de la base et que c'est une pyramide droite, la mesure de la cathète est la moitié de la mesure du côté de la base.
En associant la mesure d'une cathète avec la moitié de celle d'un côté de la base, l'autre cathète avec celle de la hauteur de la pyramide et l’hypoténuse avec celle de l'apothème, on a assez d'informations pour utiliser la relation de Pythagore : ||\begin{align} \color{#3A9A38}{a}^2 + \color{#EC0000}{b}^2 &= \color{#51B6C2}{c}^2\\\\ \color{#3A9A38}{6}^2 + \color{#EC0000}{8}^2 &= \color{#51B6C2}{a}^2\\ 100 &= \color{#51B6C2}{a}^2\\ 10\ \text{cm} &= \color{#51B6C2}{a} \end{align}||Donc, l'apothème de la pyramide est de |10\ \text{cm}.|
Lorsqu'on utilise plusieurs concepts simultanément, il faut faire attention pour ne pas s'y perdre dans l'utilisation des variables. Sur la pyramide, |\boldsymbol{\color{#51B6C2}{a}}| fait référence à l'apothème, alors que dans le théorème de Pythagore, c'est la variable |\boldsymbol{\color{#51B6C2}{c}}| qui fait référence à ce segment. Bref, pour bien comprendre les deux exemples, l'utilisation des couleurs aide grandement à associer les nombres aux segments qu'ils représentent.
Pour déterminer la mesure de la hauteur à partir de l'apothème, c’est encore le théorème de Pythagore qu’il faut utiliser.
asdf
asdf