<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>L'étude des différentes fonctions trigonométriques demande une connaissance accrue du <a href="/fr/eleves/bv/mathematiques/le-cercle-trigonometrique-m1389">cercle trigonométrique</a>.</p>
</body></html>
L'expression fonction trigonométrique est un terme général utilisé afin de désigner, entre autres, l'une ou l'autre des fonctions suivantes: sinus, cosinus, tangente, sécante, cosécante, cotangente. On appelle aussi ces fonctions des fonctions circulaires. Aussi, les fonctions trigonométriques sont d'excellents exemples de fonctions périodiques.
L'expression fonction trigonométrique réciproque est un terme général utilisé afin de désigner, entre autres, l'une ou l'autre des fonctions suivantes: arc sinus, arc cosinus, arc tangente, arc sécante, arc cosécante, arc cotangente.
Remarque: Pour que les fonctions trigonométriques réciproques soient bel et bien des fonctions, il ne faut pas oublier de limiter leur domaine et leur codomaine.
Les fonctions trigonométriques sont des fonctions périodiques. Une fonction |f(x)| est périodique s'il existe un nombre positif |P| (la période) tel que |f(x \pm P)=f(x)| pour toutes les valeurs de |x| dans le domaine de la fonction.
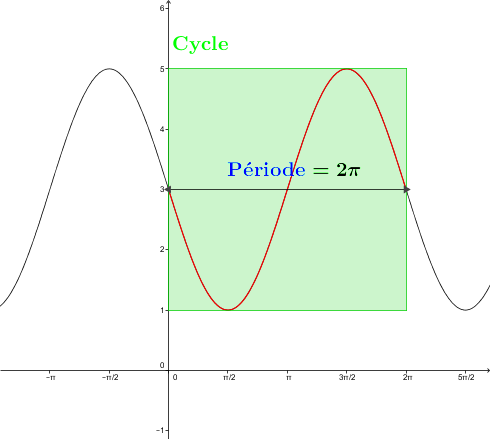
On appelle cycle d'une fonction trigonométrique la partie d'un graphique qui correspond à la plus petite portion de la courbe associée à un motif qui se répète.
On appelle période l'écart entre deux abscisses situées aux extrémités d'un même cycle.
On appelle fréquence d'une fonction trigonométrique l'inverse de la période que l'on note |\displaystyle F = \frac{1}{P}| où |P| est la période de la fonction.
Si, dans une situation, l'axe des abscisses correspond à du temps alors la fréquence correspond au nombre de cycles effectués par unité de temps.
Voici le graphique d'une fonction périodique dont la période vaut |\displaystyle P=\frac{1}{4} \text{seconde}|. L'axe des abscisses correspond à du temps en secondes.
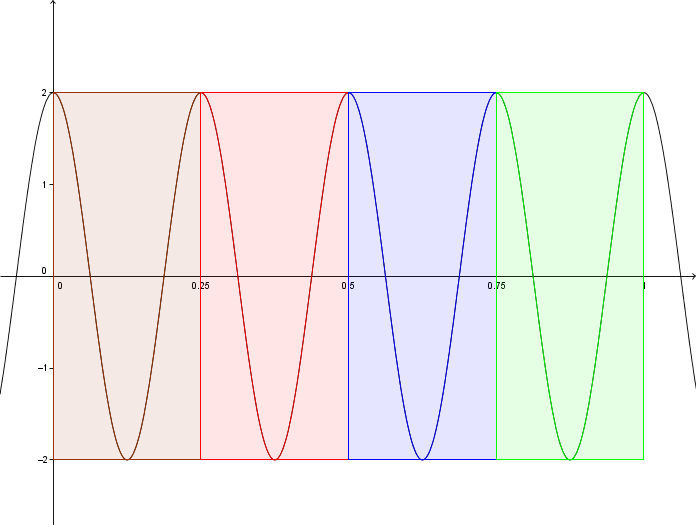
La fréquence est |\displaystyle F = \frac{1}{\frac{1}{4}} = 4 \text{ cycles/seconde}|.
On appelle amplitude d'une fonction trigonométrique la moitié de la valeur entre la différence du maximum et du minimum de la fonction.
Remarque: Cette définition s'applique aux fonctions sinus et cosinus.
L'amplitude d'une fonction trigonométrique a pour formule: ||A= \frac{\max - \min}{2}.||
On appelle déphasage la translation horizontale que subit le graphique d'une fonction sinus, cosinus ou tangente par rapport au graphique de sa fonction de base. Ce déphasage est noté par le paramètre |h|.
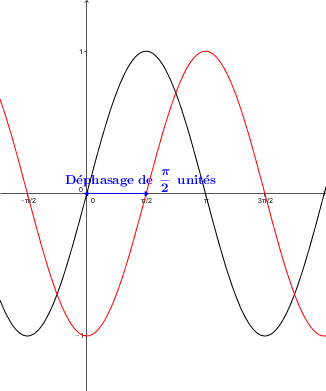
L'axe d'oscillation (ordonnée moyenne) d'une fonction sinus ou d'une fonction cosinus correspond à la droite horizontale d'équation |y=k| où |k| correspond à la translation verticale que subit le graphique par rapport à celui de sa fonction de base.

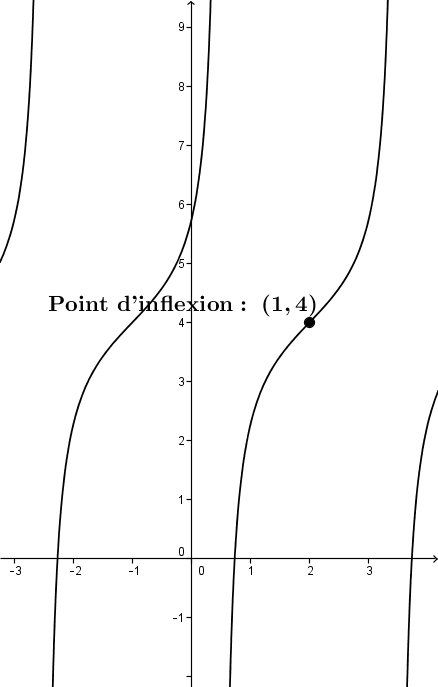
On appelle point d'inflexion un point où une courbe passe d'une forme convexe à une forme non convexe. On peut aussi dire qu'un point d'inflexion est un point où une courbe change de concavité.
Remarques :
-
Dans les fonctions sinus et tangente le point d'inflexion a pour coordonnées |(h,k)|.
-
Ce point n'est pas unique.
On appelle fonction sinusoïdale une fonction pouvant s'écrire sous la forme |f(x)=a \sin(b(x-h))+k| où |a,b \in \mathbb{R}^*| et |h,k \in \mathbb{R}|.
Les fonctions sinus et cosinus sont des fonctions sinusoïdales.