Une fonction sinus est une fonction périodique définie par l’ordonnée des points du cercle trigonométrique en fonction de la mesure des angles (en radians) du cercle.
Pour travailler avec la fonction sinus, il faut définir certains termes. De plus, d’autres notions connexes peuvent être consultées.
La règle de la fonction sinus de base est |f(x)= \sin x.|
L’animation suivante permet de voir comment passer du cercle trigonométrique à la fonction sinus de base. À chaque valeur de |\color{#333FB1}\theta| (en radians) est associé un point sur le cercle. En s’intéressant à la coordonnée en |\color{#3A9A38}y| de ces points, il est possible de tracer le graphique.
Sur l’animation, tu peux déplacer le curseur ou déplacer le point sur la courbe et observer le lien entre les deux.
-
La fonction sinus de base passe toujours par l’origine.
-
Puisque la rotation du cercle peut se faire à l’infini, le domaine de la fonction correspond à l’ensemble |\mathbb{R}.|
-
La fonction sinus possède un zéro chaque fois que l'angle |\theta| a effectué un demi-tour. Puisque la rotation du cercle est infinie, la fonction possède une infinité de zéros.||\theta \in\{\dots,\pi,\, 2\pi,\, 3\pi, \dots\}||
-
La valeur maximale est |1| et la valeur minimale est |-1,| étant donné que le rayon du cercle trigonométrique est de |1| unité.
En analysant la prochaine animation, on remarque que la fonction cosinus de base est obtenue par un déplacement horizontal de |\dfrac{\pi}{2}| unité par rapport à la fonction sinus de base. En d'autres mots, il suffit de déplacer la fonction |\cos x| de |\dfrac{\pi}{2}| unité vers la droite pour obtenir la fonction |\sin x.|
Ainsi, on en déduit l’égalité suivante.||\begin{align}\sin x&=\cos\left(x-\color{#C58AE1}h\right)\\\sin x&=\cos\left(x-\color{#C58AE1}{\dfrac{\pi}{2}}\right)\end{align}||Cette même égalité est utilisée lorsqu’on travaille avec les identités trigonométriques.
Sur l’animation, tu peux déplacer le curseur afin d’observer le déphasage entre les fonctions sinus et cosinus.
La règle de la fonction sinus transformée est |f(x)=a \sin\big(b(x-h)\big)+k.|
Le paramètre |a| est lié à l’amplitude.
Le paramètre |b| est lié à la période.
Le paramètre |h| est lié au déphasage.
Le paramètre |k| est lié à l’axe d’oscillation.
L’axe d’oscillation (aussi appelé l’ordonnée moyenne), correspond à la droite horizontale passant au milieu de la fonction.
On détermine l’axe d’oscillation d’une fonction sinus grâce au paramètre |k.| ||\color{#3a9a38}{\text{Axe d'oscillation}}: \color{#3a9a38}{y=k}||On peut aussi déterminer l’axe d’oscillation à l’aide des extrémums.||k=\dfrac{\max+\min}{2}||

Pour bien définir l’amplitude d’une fonction sinus, on a besoin de l’axe d’oscillation.
L’amplitude |\color{#fa7921}{(A)}| d’une fonction sinus correspond à la distance verticale entre l’axe d’oscillation et le maximum ou entre l’axe d’oscillation et le minimum.
On détermine l’amplitude grâce au paramètre |a.| ||\color{#fa7921}{A=\vert a\vert}||On peut aussi déterminer l’amplitude à l’aide des extrémums.||\color{#fa7921}A=\dfrac{\max-\min}{2}||

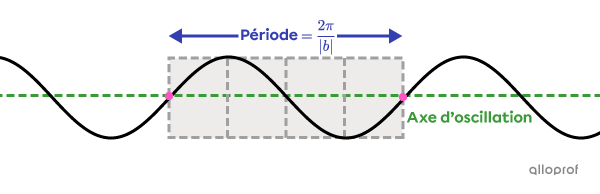
Pour définir la période, on doit repérer un cycle. Dans la fonction sinus, on choisit généralement un cycle qui débute sur un point et se termine sur un autre point situés sur l’axe d’oscillation. Cela aide à tracer la fonction sinus et à trouver sa règle.
La période |\color{#333fb1}{(p)}| correspond à l’écart entre les 2 valeurs de |x| aux extrémités d’un cycle.
On détermine la période grâce au paramètre |b.| ||\color{#333fb1}{p=\dfrac{2\pi}{\vert b\vert}}||
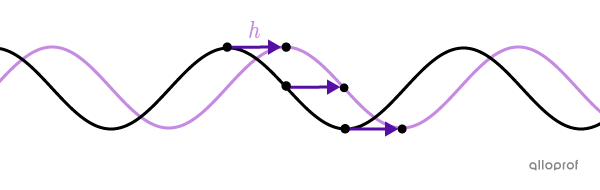
Le déphasage correspond au déplacement horizontal de la fonction sinus transformée par rapport à la fonction sinus de base.
On peut déterminer le déphasage d’une fonction sinus grâce au paramètre |h.| ||\color{#C58AE1}{\text{Déphasage}=h}||
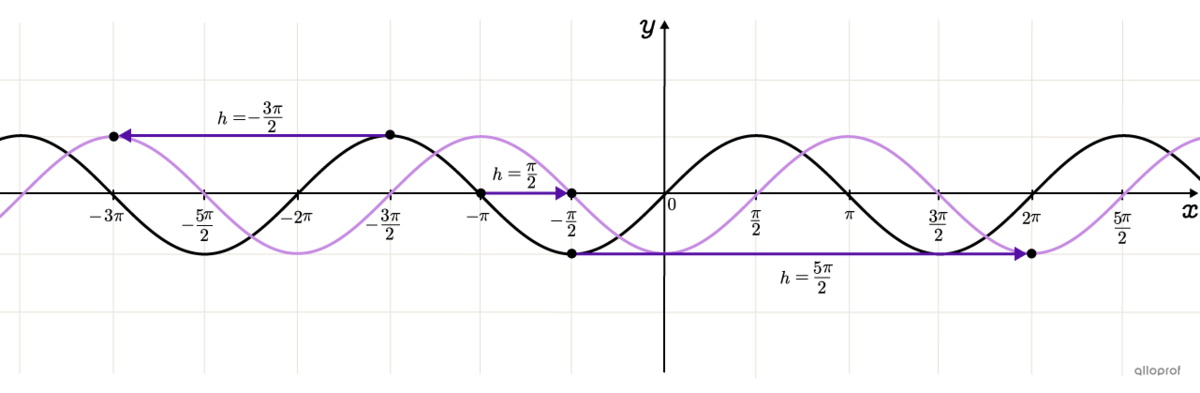
Puisque la fonction sinus est périodique, il y a plusieurs déphasages possibles pour une même fonction transformée.
Dans l’image ci-dessous, on a tracé la fonction sinus de base en noir. La fonction sinus transformée, en mauve, peut avoir subi un déphasage de |\dfrac{\pi}{2},| donc un déplacement de |\dfrac{\pi}{2}| unité vers la droite par rapport à la fonction de base.
On pourrait aussi déterminer qu’elle a subi un déphasage de |-\dfrac{3\pi}{2}| unités, donc un déplacement de |\dfrac{3\pi}{2}| unités vers la gauche, ou même de |\dfrac{5\pi}{2}| unités, vers la droite. Toutes ces options et même bien d’autres sont possibles et donnent encore la même fonction cosinus transformée.