La fonction cosinus est une fonction périodique représentée par un motif qui se répète, qu’on appelle un cycle. Pour la tracer, on construit un rectangle permettant d’encadrer un cycle, puis on le reproduit.
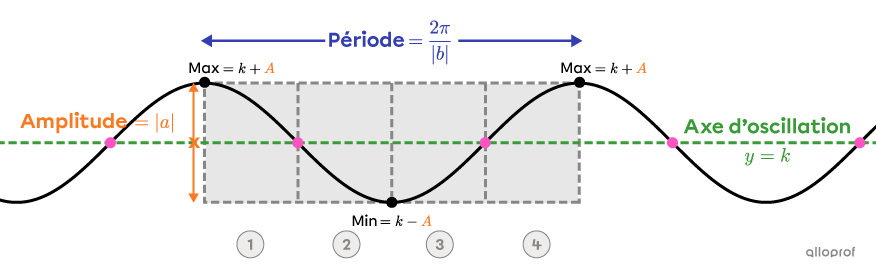
Avant de tracer cette fonction, il importe de définir certains termes et leurs liens avec les paramètres |a,| |b,| |h| et |k| de la règle de la fonction cosinus : |f(x)=a\cos\!\big(b(x-h)\big)+k.|
|
Définitions |
Liens avec les paramètres |
|---|---|
|
La période |\color{#333fb1}{(p)}| correspond à l’écart entre les 2 valeurs de |x| aux extrémités d’un cycle. |
On détermine la période grâce au paramètre |b.| ||\color{#333fb1}p=\dfrac{2\pi}{\vert b\vert}|| |
|
L’axe d’oscillation (aussi appelé ordonnée moyenne) correspond à la droite horizontale passant au milieu de la fonction. |
On détermine l’axe d’oscillation grâce au paramètre |k.| |\color{#3a9a38}{\text{Axe d'oscillation}}:| |y=k| |
|
Les points d’inflexion sont tous les points qui croisent l’axe d’oscillation. |
Dans un cycle, on retrouve 2 points d’inflexion et 3 sommets. |
|
L’amplitude |\color{#fa7921}{(A)}| correspond à la distance verticale entre l’axe d’oscillation et un extrémum. |
On détermine l’amplitude grâce au paramètre |a.| ||\color{#fa7921}A=\vert a\vert||Les extrémums se déterminent grâce à l’amplitude et au paramètre |k.| ||\begin{align}\max&=k+\color{#fa7921}A\\\min&=k-\color{#fa7921}A\end{align}|| |
Pour tracer un cycle d’une fonction cosinus, on débute à un maximum ou à un minimum, et on termine à la même hauteur. Le cycle est encadré d’un rectangle, délimité par la période et l’amplitude. Il est ensuite séparé en 4 parties égales. Chacune d'entre elles est délimitée par un point d'inflexion et un sommet.
Pour tracer une fonction cosinus, on suit les étapes suivantes.
-
Déterminer l’amplitude, la période, le déphasage et l’axe d’oscillation.
-
Déterminer le maximum et le minimum.
-
Tracer l’axe d’oscillation et des droites horizontales au maximum et au minimum.
-
Tracer le rectangle débutant à |x=h| et le séparer en 4 parties égales.
-
Déterminer le point de départ, à l’aide du signe de |a,| les autres sommets et les points d’inflexion.
Si |a| est positif, le cycle débute à |(h,k+A),| un maximum.
Si |a| est négatif, le cycle débute à |(h,k-A),| un minimum. -
Tracer un premier cycle, puis poursuivre la courbe sur le reste du plan cartésien.
Trace la fonction cosinus dont la règle est |f(x)=-2\cos\left(\dfrac{\pi}{3}(x-1)\right)-3.|
-
Déterminer l’amplitude, la période, le déphasage et l’axe d’oscillation
Selon la règle, on peut identifier les paramètres : |a=-2,| |b=\dfrac{\pi}{3},| |h=1| et |k=-3.|
|\begin{align}\color{#fa7921}A&=\vert a\vert \\&=\vert-2\vert\\ &=\color{#fa7921}{2}\end{align}|
|\begin{align}\color{#333fb1}p&=\dfrac{2\pi}{\vert b\vert}\\&=\dfrac{2\pi}{\vert\frac{\pi}{3}\vert}\\ &=2\pi \times \dfrac{3}{\pi}\\ &=\color{#333fb1}6\end{align}|
|\begin{align}\color{#a8a39e}{\text{Déphasage}}&=h\\&=\color{#a8a39e}1\end{align}|
|\begin{align}\color{#3a9a38}{\text{Axe d'oscillation}}: y&=k\\ \color{#3a9a38}{y}&\color{#3a9a38}{=}\color{#3a9a38}{-3}\end{align}|
-
Déterminer le maximum et le minimum
|\begin{align}\max&=k+\color{#fa7921}A\\&=-3+\color{#fa7921}{2}\\&=-1\end{align}|
|\begin{align} \min&=k-\color{#fa7921}A \\&=-3-\color{#fa7921}{2} \\&=-5\end{align}|
-
Tracer l’axe d’oscillation et des droites horizontales au maximum et au minimum
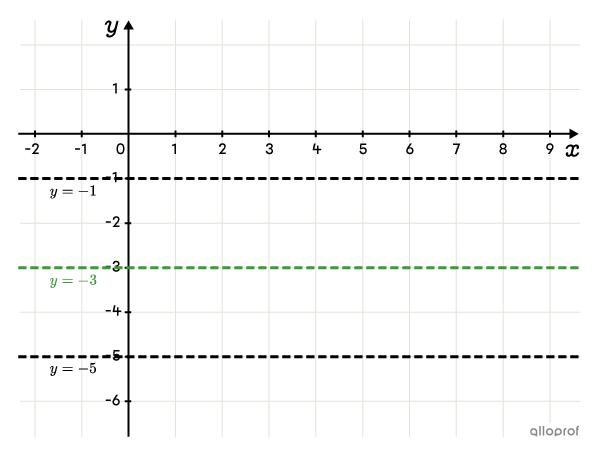
-
Tracer le rectangle débutant à |x=h| et le séparer en 4 parties égales
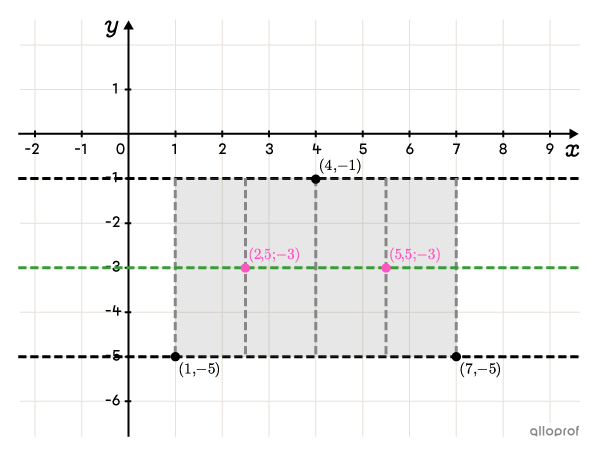
Le rectangle débute à |x=1.|Pour trouver sa longueur, on doit ajouter la période à |h.|||h+\color{#333fb1}p = 1+\color{#333fb1}6 = 7||On trace donc une droite verticale à |x=7.|
On sépare le rectangle en 2, soit à |x=4,| et encore en 2, soit à |x=2{,}5| et |x=5{,}5.|
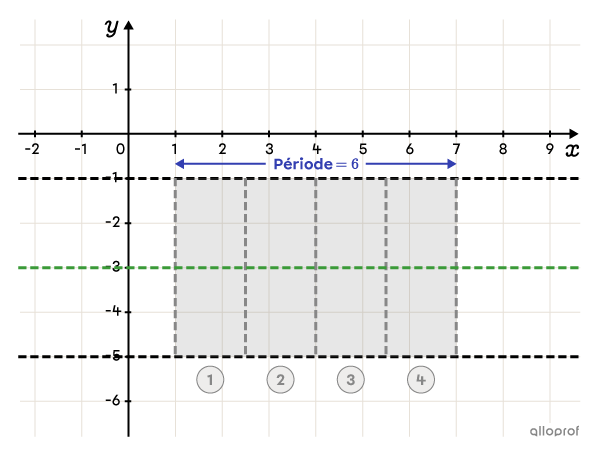
-
Déterminer le point de départ, les autres sommets et les points d’inflexion
Puisque |a| est négatif, la fonction débute à un minimum.
||\begin{align}(h&,k-\color{#fa7921}A)\\(1&,-3-\color{#fa7921}2)\\(1&,-5)\end{align}||Un quart de période plus loin, on place un point d’inflexion, soit à |(2{,}5;-3).| Un autre quart de période plus loin, on place un sommet au maximum, soit à |(4,-1).| On continue de la même façon, et on place un autre point d’inflexion à |(5{,}5;-3).| On termine à la fin du cycle avec un sommet placé au minimum, soit à |(7,-5).|
-
Tracer un premier cycle, puis poursuivre la courbe sur le reste du plan cartésien
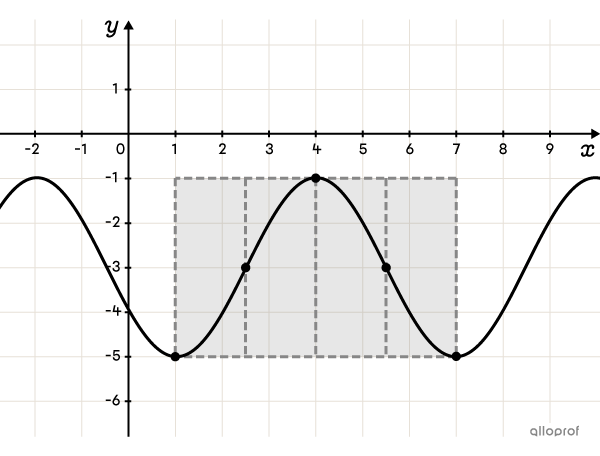
Pour graduer adéquatement les axes, il importe d’analyser la période (déterminée à l’étape 1) et les extrémums (déterminés à l’étape 2).
Graduer l’axe des |x|
-
Puisque la période est séparée en 4 parties égales, il faut idéalement que le pas de graduation en |x| soit au plus égal à |\color{#EC0000}{\dfrac{1}{4}}\color{#333fb1}p.| Dans l’exemple précédent, on a fait une graduation de |1| unité étant donné que |1<\dfrac{1}{4}p=1{,}5.|
-
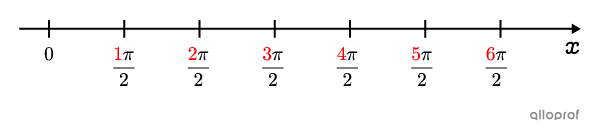
Il arrive que la période soit un multiple de |\pi,| comme lorsqu’on utilise des angles qui se mesurent en radians. Dans ces situations, on peut graduer l’axe des |x| en utilisant |\pi.| Par exemple, si la période est de |\color{#333fb1}{2\pi},| la graduation pourrait être de |\dfrac{\pi}{2}.|||\color{#EC0000}{\dfrac{1}{4}}\color{#333fb1}p=\color{#EC0000}{\dfrac{1}{4}}{\color{#333fb1}{(2\pi)}}=\dfrac{\pi}{2}||
À ce moment, on obtient la graduation suivante.
Par la suite, si on le désire, on peut réduire les fractions.
Graduer l’axe des |y|
On gradue l’axe des |y| en fonction du maximum et du minimum. Il suffit de trouver une graduation qui permet d’avoir assez d’espace pour tracer un cycle.
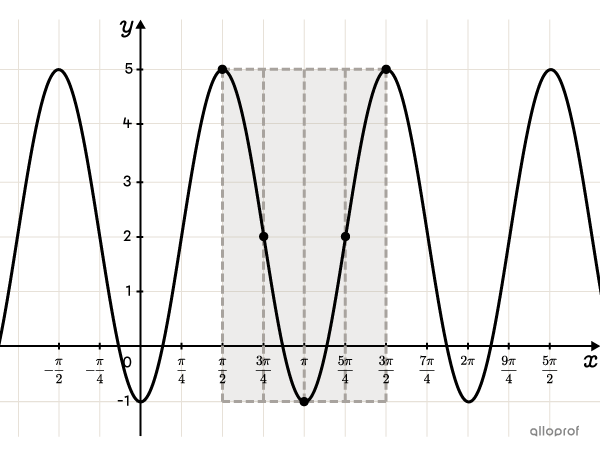
Trace la fonction cosinus dont la règle est |f(x)=3\cos\!\bigg(2\left(x-\dfrac{\pi}{2}\right)\!\bigg)+2.|
-
Déterminer l’amplitude, la période, le déphasage et l’axe d’oscillation
Selon la règle, on peut identifier les paramètres : |a=3,| |b=2,| |h=\dfrac{\pi}{2}| et |k=2.|
|\begin{align}\color{#fa7921}A&=\vert a\vert \\&=\vert 3\vert\\ &=\color{#fa7921}{3}\end{align}|
|\begin{align}\color{#333fb1}p&=\dfrac{2\pi}{\vert b\vert}\\&=\dfrac{2\pi}{\vert2\vert}\\&=\color{#333fb1}{\pi}\end{align}|
|\begin{align}\color{#a8a39e}{\text{Déphasage}}&=h\\&=\color{#a8a39e}{\dfrac{\pi}{2}}\end{align}|
|\begin{align}\color{#3a9a38}{\text{Axe d'oscillation }}: &\ y=k\\ &\ \color{#3a9a38}{y=2}\end{align}|
-
Déterminer le maximum et le minimum
|\begin{align}\max&=k+\color{#fa7921}A\\&=2+\color{#fa7921}{3}\\&=5\end{align}|
|\begin{align}\min&=k-\color{#fa7921}A\\&=2-\color{#fa7921}{3}\\&=-1\end{align}|
-
Tracer l’axe d’oscillation et des droites horizontales au maximum et au minimum
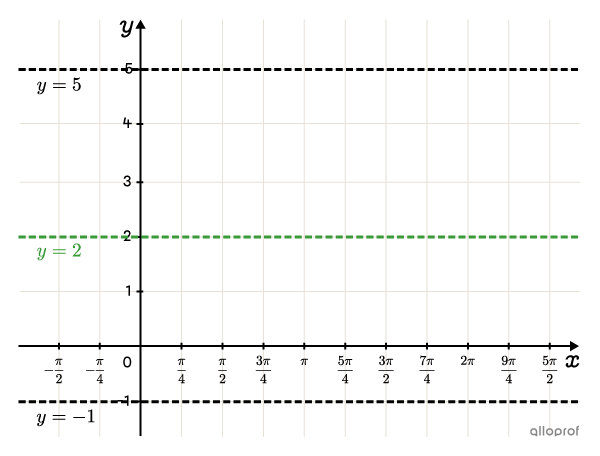
Dans l’image ci-contre, on a tracé l’axe d’oscillation et des droites aux valeurs maximale et minimale.Puisque la période est |\pi,| la graduation en |x| choisie est |\color{#333fb1}{\dfrac{\pi}{4}}.|||\color{#EC0000}{\dfrac{1}{4}}\color{#333fb1}p=\color{#EC0000}{\dfrac{1}{4}}{\color{#333fb1}{(\pi)}}=\dfrac{\pi}{4}||
-
Tracer le rectangle débutant à |x=h| et le séparer en 4 parties égales
Le rectangle débute à |x=\dfrac{\pi}{2}.|Pour trouver sa longueur, on doit ajouter la période à |h.|||\begin{align}h+\color{#333fb1}p&=\dfrac{\pi}{2}+\color{#333fb1}{\pi}\\&=\dfrac{\pi}{2}+\dfrac{2\pi}{2}\\&=\dfrac{3\pi}{2}\end{align}||On sépare le rectangle en 2, soit à |x=\pi,| et encore en 2, soit à |x=\dfrac{3\pi}{4}| et |x=\dfrac{5\pi}{4}.|
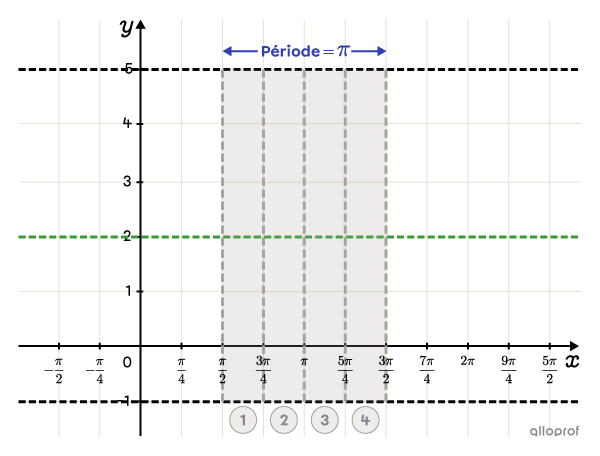
-
Déterminer le point de départ, les autres sommets et les points d’inflexion
Puisque |a| est positif, la fonction débute à un maximum.||(h,k+\color{#fa7921}A)\\ \left(\dfrac{\pi}{2},2+\color{#fa7921}3\right)\\ \left(\dfrac{\pi}{2},5\right)||Un quart de période plus loin, on place un point d’inflexion, soit à |\left(\dfrac{3\pi}{4},2\right)\!.| Un autre quart de période plus loin, on place un sommet au minimum, à |(\pi,-1).| On continue de la même façon et on place un autre point d’inflexion à |\left(\dfrac{5\pi}{4},2\right)\!.| On termine à la fin du cycle avec un sommet placé au maximum, soit à |\left(\dfrac{3\pi}{2},5\right)\!.|
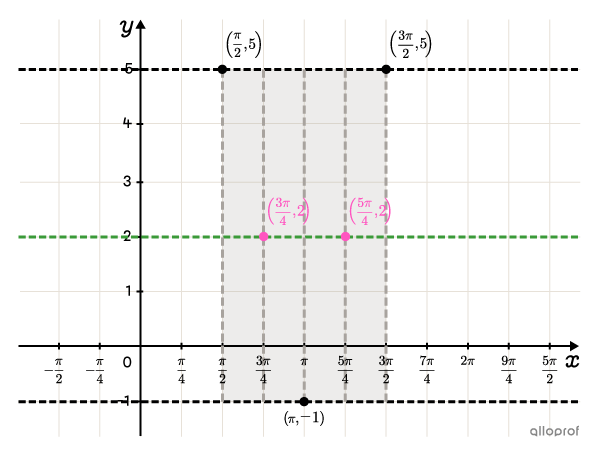
-
Tracer un premier cycle, puis poursuivre la courbe sur le reste du plan cartésien