Dans l'animation interactive suivante, tu peux modifier les paramètres |a,| |h| et |k| de la fonction valeur absolue et observer leurs effets sur les propriétés de la fonction. Après cette exploration, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions concernant les propriétés de la fonction.
| PROPRIÉTÉS | CARACTÉRISTIQUES FONCTION VALEUR ABSOLUE TRANSFORMÉE ||f(x)=\color{red}{a}\mid x-\color{blue}{h} \mid + \color{green}{k}|| |
|---|---|
| Domaine | |x \in \mathbb{R}| |
| Codomaine (image) |
Si |a>0,| alors |[k, \infty[| Si |a<0,| alors |]-\infty,k]| |
| Ordonnée à l'origine | Il faut remplacer |x| par |0| dans l'équation et calculer la valeur du |y.| Cette valeur sera l'ordonnée à l'origine. |
| Abscisse à l'origine (zéro de la fonction) |
Si |a| et |k| sont de signes diffférents, alors il y aura deux zéros distincts. Si |k=0,| alors il y aura un seul zéro. Si |a| et |k| sont du même signe, alors il n'y aura pas de zéro. |
| Sommet | |(h,k)| |
| Croissance et décroissance |
Si |a>0,| alors la fonction est décroissante sur l'intervalle |]-\infty,h]| et croissante sur l'intervalle |[h,\infty[.| Si |a<0,| alors la fonction est croissante sur l'intervalle |]-\infty,h]| et décroissante sur l'intervalle |[h,\infty[.| |
| Extrémums | |k| Si |a<0,| |k| est un maximum. Si |a>0,| |k| est un minimum. |
| Signes | Si |a>0| et |k>0,| alors il n'y a pas de zéro et la fonction est positive pour tous les |x.| Si |a<0| et |k<0,| alors il n'y a pas de zéro et la fonction est négative pour tous les |x.| Si |a>0| et |k=0,| alors il y a un seul zéro |(h,0)| et la fonction est positive pour tous les |x.| Si |a<0| et |k=0,| alors il y a un seul zéro |(h,0)| et la fonction est négative pour tous les |x.| Si |a>0| et |k<0,| alors il y a deux zéros et la fonction est négative pour l'intervalle des |x| compris entre les deux zéros et elle est positive pour le reste des |x.| Si |a<0| et |k>0,| alors il y a deux zéros et la fonction est positive pour l'intervalle des |x| compris entre les deux zéros et elle est négative pour le reste des |x.| |
| Axe de symétrie | La fonction valeur absolue a un axe de symétrie. |x=h| |
| Asymptotes | Il n'y a pas d'asymptote pour la fonction valeur absolue. |
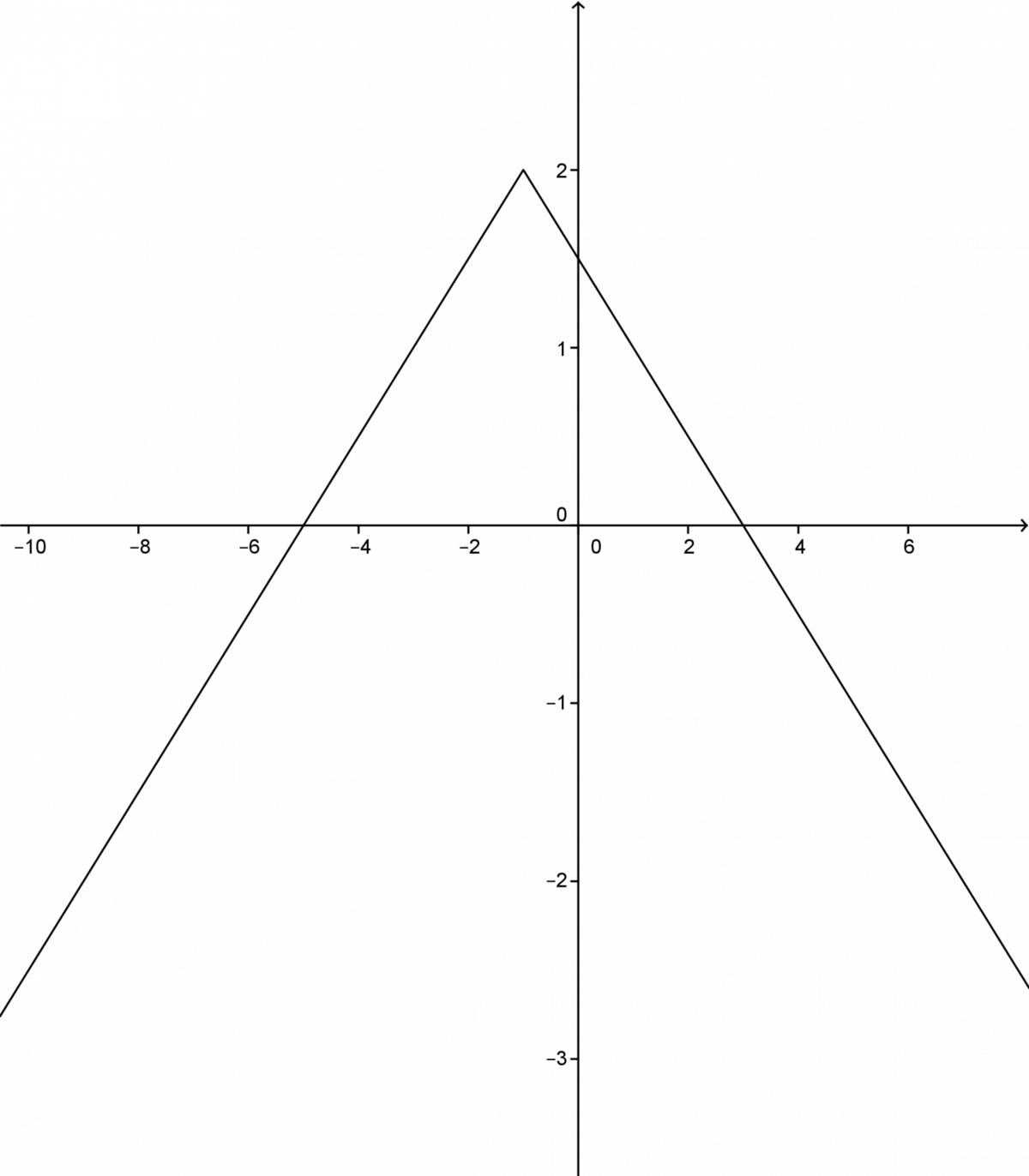
Déterminez les propriétés de la fonction valeur absolue |f(x) = \displaystyle - \frac{1}{2} \mid x+1 \mid +2.|
Il est utile de tracer une esquisse graphique de la fonction.
Le sommet est |(-1,\ 2)| et la fonction est ouverte vers le bas, car |a<0.|
-
Le domaine de la fonction est l'ensemble des nombres réels que l'on note | \mathbb{R}.|
-
L'image de la fonction correspond à l'intervalle |]- \infty, 2].|
-
Pour calculer l'ordonnée à l'origine, il suffit de remplacer |x| par |0.| ||\begin{align}f(0) &= \displaystyle - \frac{1}{2} \mid 0 + 1 \mid +2\\ f(0) &= \displaystyle \frac{3}{2}\end{align}||L'ordonnée à l'origine vaut donc | \displaystyle \frac{3}{2}.|
-
Pour calculer les zéros de la fonction, il suffit de remplacer |f(x)| par 0 puis d'isoler |x.| ||\begin{align} 0 &= \displaystyle - \frac{1}{2} \mid x+1 \mid +2\\ -2 &= \displaystyle - \frac{1}{2} \mid x +1 \mid\\ 4 &= \mid x +1 \mid \end{align}|| Rendu ici, on utilise la définition de la valeur absolue. ||\begin{align}4 &=x+1 &-4 &= x+1 \\ 3 &=x &-5 &= x\end{align}|| Les deux zéros sont donc |-5| et |3.|
-
Variation : la fonction est croissante de |]- \infty, -1]| et elle est décroissante de |[-1, + \infty[|.
-
Extrémums : le |a| étant négatif, la fonction possède un maximum en 2.
-
Signes : en utilisant l'ouverture de la fonction et les zéros trouvés précédemment, on peut déterminer les signes de la fonction :
-
Elle sera positive sur |[-5,3].|
-
Elle sera négative sur |]-\infty,-5] \cup [3, +\infty[.|
-
-
L'équation de l'axe de symétrie est |x=-1.|