Il est possible d'établir des sous-classes des nombres entiers naturels |(\mathbb{N})| en fonction de certaines de leurs caractéristiques.
Un nombre pair est un nombre entier divisible par |\boldsymbol{2}.|
Un nombre pair représente une quantité que l’on peut regrouper en paquets de |2| unités sans obtenir de reste. En d'autres mots, on peut définir un nombre pair comme un nombre entier divisible par |2,| dont le quotient de la division par |2| est aussi un nombre entier (ex.: |6\div 2 = 3|).
Avec le nombre |8,| on peut faire |4| paquets de |2| unités sans qu'il n'y ait de reste.
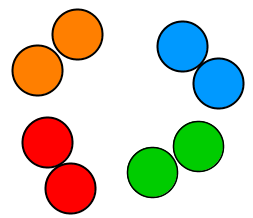
De plus, on remarque que le nombre |8| est divisible par |2.| ||8\div 2=4||
Donc, le nombre |8| peut être qualifié de nombre pair.
On peut reconnaitre un nombre pair grâce au chiffre occupant la position des unités. En effet, les nombres pairs ne peuvent que se terminer par les chiffres |0,2,4,6| et |8.|
Les nombres suivants sont des nombres pairs car ils se terminent par un des 5 chiffres possibles à la position des unités. ||2\ 00\color{#3b87cd}{0},\ 10\color{#3b87cd}{4},\ \color{#3b87cd}{4},\ 3\color{#3b87cd}{2},\ 6\color{#3b87cd}{6},\ 19\color{#3b87cd}{8},\ 700\ 00\color{#3b87cd}{0}||
Un nombre impair est un nombre entier non divisible par |\boldsymbol{2}.|
Un nombre impair représente une quantité que l’on ne peut pas regrouper en paquets de |2| sans obtenir de reste. La division d'un nombre impair par |2| donnerait un nombre fractionnaire ou décimal comme réponse.
Avec le nombre |7,| on n’arrive pas à faire des paquets de |2| sans reste. On aura |3| paquets de |2| unités et un reste d’une unité.
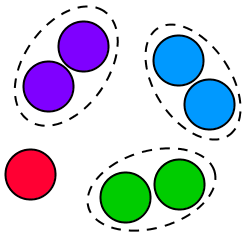
On peut reconnaitre un nombre impair grâce au chiffre occupant la position des unités. En effet, les nombres impairs ne peuvent que se terminer par les chiffres |1,| |3,| |5,| |7,| et |9.|
Les nombres suivants sont des nombres impairs, car ils se terminent par un des 5 chiffres possibles à la position des unités.||10\color{#3a9a38}{5},\ 5\color{#3a9a38}{3},\ 1\color{#3a9a38}{7},\ \color{#3a9a38}{9},\ 2\color{#3a9a38}{1},\ 5\color{#3a9a38}{9},\ 10\color{#3a9a38}{3},\ 98\ 00\color{#3a9a38}{7}||
Un nombre premier est un nombre naturel qui n’a que 2 diviseurs positifs différents, c’est-à-dire |1| et lui-même.
Le nombre 0
Le nombre |\boldsymbol{0}| possède une infinité de diviseurs. ||0\div1=0\\0\div2=0\\0\div3=0\\...||De plus, le nombre |0| ne peut pas être divisé par lui-même, car la division par |0| est une opération non définie. Il n'est donc pas un nombre premier.
Le nombre 1
Le nombre |\boldsymbol{1}| n'est pas considéré comme étant un nombre premier, car il ne possède pas 2 diviseurs différents. En effet, il n'a que |1| comme diviseur.
Exemple 1
Le nombre |11| est-il un nombre premier?
Les 2 seuls nombres qui divisent |11| sans laisser de reste sont |1| et |11.|
Donc, |11| est un nombre premier.
Exemple 2
Le nombre |29| est-il un nombre premier?
Les 2 seuls nombres qui divisent |29| sans laisser de reste sont |1| et |29.|
Donc, |29| est un nombre premier.
Exemple 3
Le nombre |49| est-il un nombre premier?
|49| est divisible par |1,| |7| et |49.| Comme il possède 3 diviseurs différents, |\boldsymbol{49}| n'est pas un nombre premier. On dira de |49| qu'il est un nombre composé.
De par la définition, il est possible de dresser une liste des nombres premiers contenus dans notre système de numération.
| Liste des nombres premiers inférieurs à |1\,000| | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| |2| | |3| | |5| | |7| | |11| | |13| | |17| | |19| | |23| | |29| |
| |31| | |37| | |41| | |43| | |47| | |53| | |59| | |61| | |67| | |71| |
| |73| | |79| | |83| | |89| | |97| | |101| | |103| | |107| | |109| | |113| |
| |127| | |131| | |137| | |139| | |149| | |151| | |157| | |163| | |167| | |173| |
| |179| | |181| | |191| | |193| | |197| | |199| | |211| | |223| | |227| | |229| |
| |233| | |239| | |241| | |251| | |257| | |263| | |269| | |271| | |277| | |281| |
| |283| | |293| | |307| | |311| | |313| | |317| | |331| | |337| | |347| | |349| |
| |353| | |359| | |367| | |373| | |379| | |383| | |389| | |397| | |401| | |409| |
| |419| | |421| | |431| | |433| | |439| | |443| | |449| | |457| | |461| | |463| |
| |467| | |479| | |487| | |491| | |499| | |503| | |509| | |521| | |523| | |541| |
| |547| | |557| | |563| | |569| | |571| | |577| | |587| | |593| | |599| | |601| |
| |607| | |613| | |617| | |619| | |631| | |641| | |643| | |647| | |653| | |659| |
| |661| | |673| | |677| | |683| | |691| | |701| | |709| | |719| | |727| | |733| |
| |739| | |743| | |751| | |757| | |761| | |769| | |773| | |787| | |797| | |809| |
| |811| | |821| | |823| | |827| | |829| | |839| | |853| | |857| | |859| | |863| |
| |877| | |881| | |883| | |887| | |907| | |911| | |919| | |929| | |937| | |941| |
| |947| | |953| | |967| | |971| | |977| | |983| | |991| | |997| | | |
Par contre, les nombres entiers naturels se poursuivent jusqu'à l'infini. Ainsi, il est pratiquement impossible de dresser une liste exhaustive de tous les nombres premiers.
Pour certains mathématiciens et chercheurs, ce concept présente un défi en soi. Même s'il est théoriquement impossible de faire la liste de tous les nombres premiers, on peut quand même essayer de trouver celui avec la plus grande valeur.
En 2016, une équipe de chercheurs de l'Université de Central Missouri a mis sur pied un système informatique qui leur a permis de trouver un nombre premier contenant 22 338 618 chiffres, ce qui le rend pratiquement impossible à lire!
Un nombre composé est un nombre qui a 3 diviseurs positifs ou plus.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>En d'autres mots, un nombre composé peut être exprimé comme le produit de deux nombres premiers ou plus (identiques ou distincts). Ainsi, un nombre composé peut être décomposé en <a href="/fr/eleves/bv/mathematiques/la-factorisation-d-un-nombre-m1529">facteurs premiers</a>.</p>
</body></html>
On nomme cette décomposition en facteurs premiers une factorisation première.
Le nombre 0
Même si le nombre |0| possède une infinité de diviseurs, il n'est pas considéré comme un nombre composé puisqu'il ne possède aucune factorisation première.
Le nombre 1
Le nombre |1| n'est pas considéré comme un nombre composé, car il ne possède pas au moins 3 diviseurs.
Ces 2 nombres sont les seuls nombres entiers qui ne sont ni des nombres premiers ni des nombres composés.
Tous les nombres entiers naturels dont la valeur est plus grande que |1| qui ne sont pas des nombres premiers sont conséquemment des nombres composés.
Exemple 1
Les diviseurs positifs de |9| sont : |1,| |3| et |9.|
Puisque le nombre |9| possède 3 diviseurs, on dira que |9| est un nombre composé. Comme il est composé, ce nombre peut être exprimé comme un produit de nombres premiers (facteurs premiers).||9=3\times 3||
Exemple 2
Les diviseurs positifs de |24| sont : |1,| |2,| |3,| |4,| |6,| |8,| |12| et |24.|
Puisque le nombre |24| possède plus de 3 diviseurs, on dira que |24| est un nombre composé. Comme il est composé, ce nombre peut être exprimé comme un produit de nombres premiers (facteurs premiers).||24=2\times2\times2\times3||
Exemple 3
Les diviseurs positifs de |13| sont : |1| et |13| seulement.
Puisque le nombre |13| ne possède pas 3 facteurs ou plus, il n'est pas un nombre composé. En fait, |13| est un nombre premier.
Un nombre parfait est un nombre naturel dont la somme de ses diviseurs (positifs), excluant le nombre lui-même, est égale au nombre lui-même.
Exemple 1
|6| est un nombre parfait, car la somme de ses diviseurs, sauf |6,| est égale à lui-même.||1+2+3 = 6||
Exemple 2
|28| est un nombre parfait, car la somme de ses diviseurs, sauf |28,| est égale à lui-même.||1+2+4+7+14 = 28||
Exemple 3
|10| n'est pas un nombre parfait, car la somme de ses diviseurs, sauf |10,| n'est pas égale à lui-même.||1+2+5 \color{#ec0000}{\neq}10||
Un nombre carré est un nombre pouvant s'exprimer sous la forme |n^2,| où |n| est un nombre entier naturel.
En d'autres mots, il s'agit d'un nombre qui résulte du produit d'un nombre entier naturel par lui-même.
Géométriquement parlant, les nombres carrés peuvent être représentés par des points disposés en carré.
Voici la liste des 4 premiers nombres carrés.
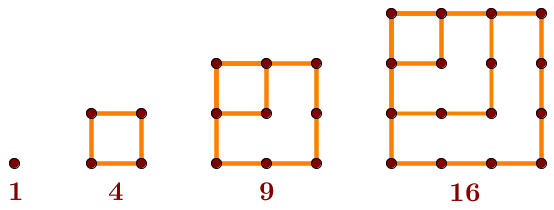
On remarque que ces nombres peuvent s'exprimer sous la forme |n^2.| ||\begin{align}1&=1^2\\ 4&=2^2\\ 9&=3^2\\ 16&=4^2\end{align}||
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span><a href="/fr/eleves/bv/mathematiques/les-nombres-carres-et-cubiques-m1042">Les nombres carrés et cubiques</a></span></p>
</body></html>
Un nombre triangulaire est un nombre pouvant être représenté par des points disposés en forme de triangle régulier.
Voici la liste des 4 premiers nombres triangulaires.
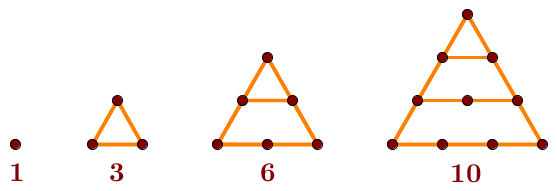
Les nombres carrés et triangulaires sont ce qu'on appelle des nombres polygonaux. Ce sont des nombres qui peuvent être représentés par des points disposés en forme de figures géométriques régulières.